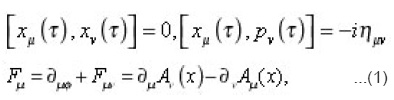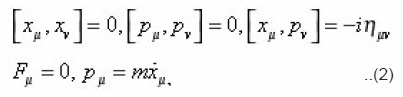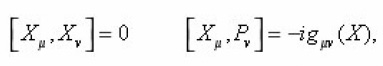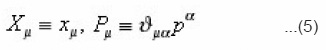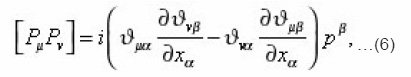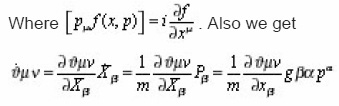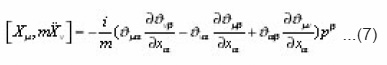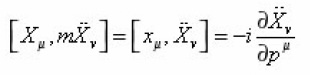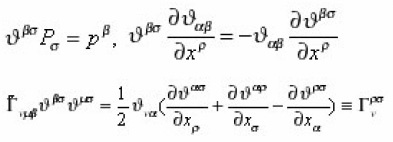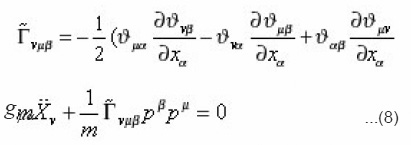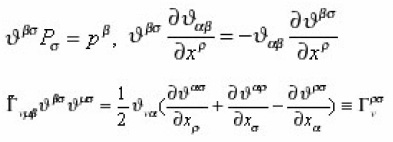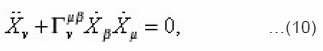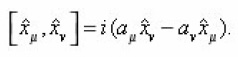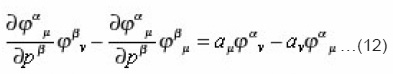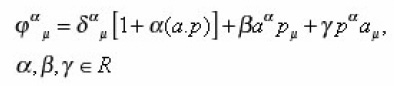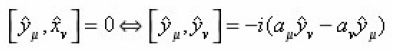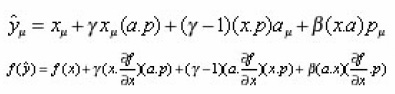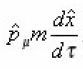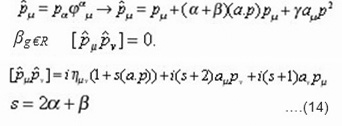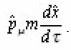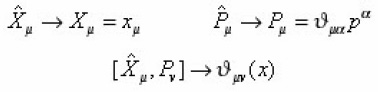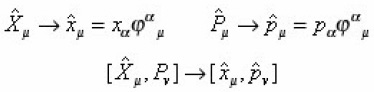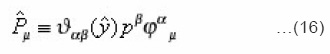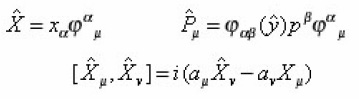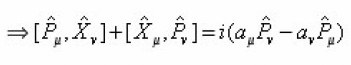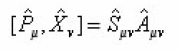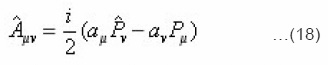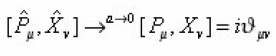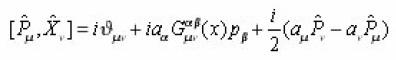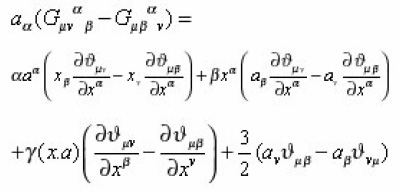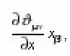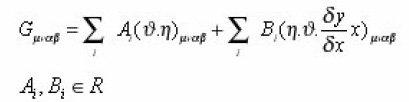Dharmendra Kumar1 and Sunil KumarYadav2
¹Department of Physics, K.B. Womens College, Madhepura, India.
²Department of Physics, C.N. College, Ramgarh, India.
DOI : http://dx.doi.org/10.13005/msri/090117
Article Publishing History
Article Received on : 12 June 2012
Article Accepted on : 05 July 2012
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:
The present study aims to derive modified geodesic equation in non-commutative space time. Snyder developed a model for non-commutative space time which provides a suitable technique of quantum structure of the space. We extend Tetrad formulation of general relativity to non-commutative case for complex gravity models. We derive geodesic equation on the k-space time in Non-commutative space, which is a generalization of Feynman’s approach. It has been shown that the homogeneous Maxwell’s equations may be derived by starting with the Newton’s force equation and generalized to relativistic. We show that the geodesic equation in the commutative space time is a suitable for generalization to κ -space time in κ -deformed space time. It shown that the κ-dependent correction to geodesic equation is cubic in velocities.
KEYWORDS:
Geodesic; Non-commutative; Space time; Newtonian; Gravity model; Feynmann; Deformed
Copy the following to cite this article:
Kumar D, Yadav S. K. On Characterization of Non-commutative Minkowski Space Time. Mat.Sci.Res.India;9(1)
|
Introduction
Several field theory models on k- space time have been constructed , using different techniques such as by F. Mejer and J Lukierski specially in, scalar field theory on k-Minkowski space. It has been shown by S. Tanimutra that in the flat space time, Feynman approach and minimal coupling method are equivalent which is usefull to derive the general equation of motion for a charged particle. We discuss here the applicability of Feynman approach for the case of general relativity, resulting in the derivation of the geodesic equation. We generalize the procedure for k-Minkowski space. We obtain here corrections to the geodesic equation due to the k-deformation of space time , up to the first order in the deformation parameter. WE know that a relativistic particle of mass m and electric charge e is described by in 4D-Minkowski space, where xμ(τ) in 4D- Minkowski space, where τ is a parameter. Let us write the following relations
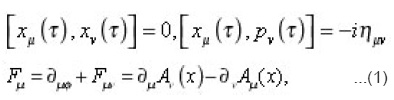
Where pμ = mx + eAμ is the canonical momentum operator, Fμ = mx, the forceμν the electromagnetic strength tensor, Aμ is a gauge field and Φ(x) is an arbitrary function odfx. We deal with gravity only, which do not require the gauge field. We only evaluate particles with no electric charge, which for a neutral particle we obtain the following equations.
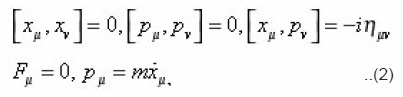
Φ(x) = 0 to find the correct geodesic equation.M. Montesinos obtained that the generalization from flat to curved space by taking Eq.(1) as valid in a local Lorenz frame of reference and effect of gravity is brought in by replacing the Minkowskian metric nμν with an arbitrary metric gμν (X). He has shown that this assumption leads to geodesic equation. We choose
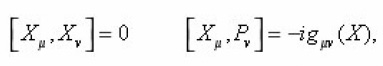
Let us assume that the ‘metric’ gμ(x) is a function of operator X which is a symmetric tensor.
Theorem (Generalization of Commutative Space Time )
Let Xμ(τ) be a new position operator and pμ(τ) is the corresponding conjugate momenta, mXμ = Pμ, then solution of equation may be obtain in terms of the operators given in (2). Proof
We construct operators X and P expressed as follows.
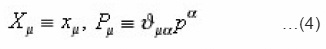
Where xμ and pν satisfy relation. By taking the derivative with respect to of Eqs.(4), we obtain the following relation.
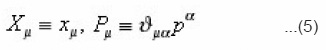
Where pμ = mXμ . Combining equations (5) and (2) we obtain
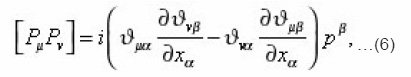
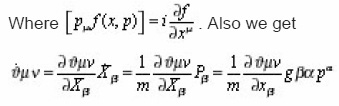
Combining equations (3), (5), (6), we obtain the equation
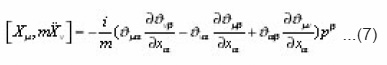
By choosing the operator X such that is Xμ = Xμ (x,p), LHS of (7) reduces to the equation
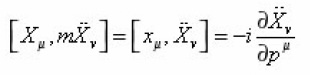
We now integrate Eq. (6) over pμ which gives the relation
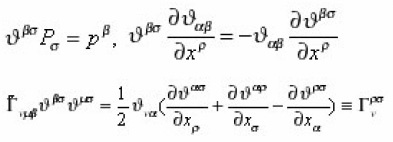
By taking Gν(x) = 0 we get
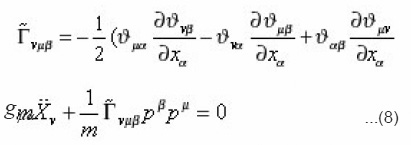
Where all Jacobi identities are satisfied. Eq. (6) is similar to the Christoffel symbol in general relativity, and Eq. (8) is similar to the geodesic equation. Let us assume that ‘metric’ is invertible and define an inverse of the symmetric tensor by the following relation
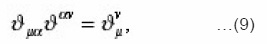
Combining the equations (4), (7) and (9) we get
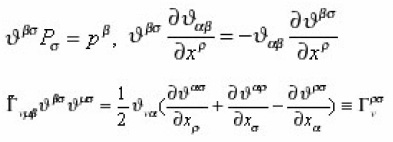
Where
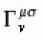
is really the Christoffelsymbol, we get the geodesic equation
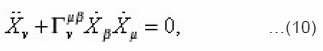
Where vgμ tensor is treated only as a symmetric tensor with an inverse defined in Eq. (10).
Theorem (Derivation of Geodric Equation In K- Minkowski Space Time)
We derive the geodesic equation for a particle moving in the non-commutative curved space time and analyze the k-Minkowski deformations of gravity. The methods taken here use k-Minkowskideformations on the flat space time. It is further generalized to k-deformed space time with arbitrary metric.
Proof
Let us define k-Minkowski space by the relation
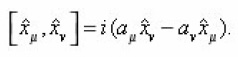
Operators
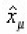
care expressed in terms of operators x and using the derivations due to J. Lukerki and H. Ruegg. We get
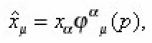
Where
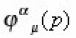
satisfy the identity
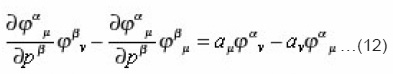
Let us solve Eq. (11) up to the first order in deformation parameter a, which gives
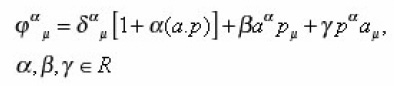
Where parameters of the realization a, b, and g satisfy the a constraint
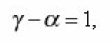
Let us define an operator
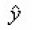
which commutes with
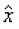
, i.e.
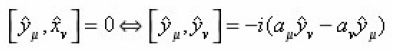
Any function of ˆy also commutes with

Where we take only first order in the modified form of give
and
up to the first order in
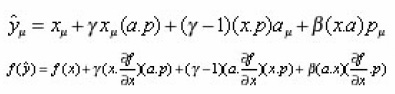
The canonical momentum operator ( in e = 0 case )
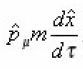
as derived by the relation
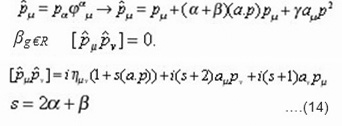
Hence , we conclude that construction due to E. HariKumar via Feynman approach satisfy all Jacobi identities. The condition that comes by taking the derivative of Eq. (12) with respect to τ is
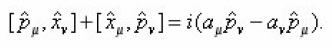
Hence the geodesic equation in the k- Minkowski space time is established.
Theorem ( k-Dependent Corrections to the Geodesic Equation )
Proof
Let us choose the conjugate pairs (x , p ) and for flat non-commutative space time,
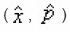
in commutative and non- commutative space respectively. It is shown that all the operators in the flat non-commutative space time are expressed in terms of x , p and deformation parameter a. For the non-commutative space time with curvature. Let us construct it as functions of x , p and deformation parameter . In case of neutral particles , conjugate momenta is given by
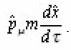
We derive the corrections to the geodesic equation due to the k- deformation of space time. Let us consider the relation.
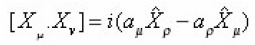
Where
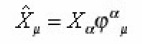
And
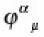
satisfies Eq. (12).
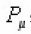
satisfy all the Jacobi Indentifies and the relation
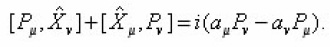
But in the limit a ®0, it implies that
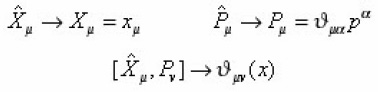
By taking limit
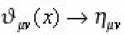
we get the following relations
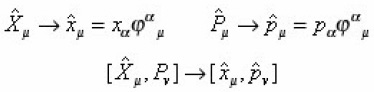
Combining these equation, and comparing it with (13) & (14)
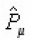
substitute
with a function that commutes with
That is with
Thus , we obtain the required form
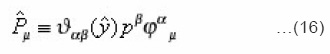
By an appropriate application of (14), we find that this construction satisfioes all Jacobi identities and Eq. (15) is also satisfied to all orders in a
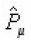
Hence , get its modified form as follows
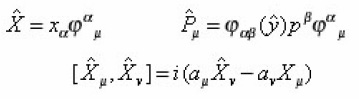
An alternative construction of the operator up to the first order in the deformation parameter may be obtained by differentiating Eq. (17) with respect to τ.
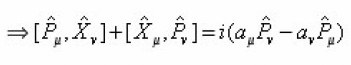
It satisfies antisymmetric part of
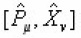
We write it as follows
Where
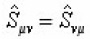
and
Combining Eq. (16) and (17), We get
By taking the limit a a →0, we obtain
Hence , the case of up to the first order in the deformation parameter a
i.e.
Here
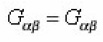
and we get the following relations
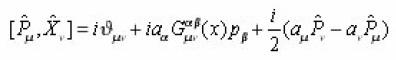
We get constraints on
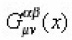
that the Jacobi identities must be satisfied up to the first order in a.
We get
Let us construct
from
Hence
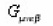
is determined by the parameters a and b and four
More free parameters. This general used form but valid up to the first order in the deformation
parameter a. The construction
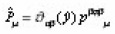
where is the special case of this general procedure.
Conclusion
The principal characteristic of this approach is that all the corrections depend on the choice of realization of the parameters on the mass of the test particle.
We analysed here the a-dependent correction to the Newtonian limit of the geodesic equation which shows that the Newtonian force/potential remains radial, but depends on the mass of the test particle.
We have shown here that the κ-deformed commutation relations between phase space variables induce modified incertainty relations
It has been shown that the commutative limit
gives rise to the metric
and by analogy, we interpret
non- commutative metric .
References
- H.S Synder, Phys. Rev. 7: 1-38 (1947).
- R. Wald, General relativity University of Chicago Press (1948).
- Jacques Bros., The Geometry of Relativistic Space time Seminaire Poincare1 (1-45) (2005).
- S. Caroll, Space time and Geometry an Introduction to general relativity (2003).
- J. Lukierski and H. Ruegg. A. Nowieki Phys. Lett. B293: 344 (1992)
CrossRef
- S. Kresic-Jurie, S. Meljanae and M. Stojic J. Phys. A42: 365204 (2009)
CrossRef
- S. Tanimura, Annals of Physics 220: 229 (1992).
CrossRef
- E. HariKumar, M., Mod Sivakumar and N. Srinivas . Phys. Lett. A26: 1103 (2011)
Views: 135
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Material Science Research India An International Peer Reviewed Research Journal
Material Science Research India An International Peer Reviewed Research Journal