Views 
  

 Open Access -   Download full article: 

Vibrational Spectra of Aniline in Gas Phase: An Ab-Initio Study

S. D. S. Chauhan, A.K. Sharma, Rakesh Kumar, D. Kulshreshtha, R. Gupta, P. K. S. Chauhan1* and O. P. Singh

Department of Physics, Chemistry, Paliwal (P.G.) College, Shikohabad - 205 135, India.

Corresponding Author E-mail: sahahdevsinghchauhan@yahoo.in

DOI : http://dx.doi.org/10.13005/msri/070215

Article Publishing History
Article Received on : 25 May 2010
Article Accepted on : 29 Jun 2010
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:

Vibrational frequencies of aniline in gas phase have been calculated and each of their modes of vibration assigned properly at RHF and DFT with 6-31G(d) basis set. In the present study, it has been observed that the 6-31G(d) basis set at both RHF and DFT levels of calculations provides better agreement to the experimental findings as compared to other basis sets. Simultaneously, Density functional theory is found to be superior to its counterpart Hartree Fock method.

KEYWORDS: Vibrational frequency; Aniline; IR; HF; DFT; Ab-initio

Copy the following to cite this article:

Chauhan S. D. S, Sharma A. K, Kumar R, Kulshreshtha D, Gupta R, Chauhan P. K. S, Singh O. P. Vibrational Spectra of Aniline in Gas Phase: An Ab-Initio Study. Mat.Sci.Res.India;7(2)

Copy the following to cite this URL:

Chauhan S. D. S, Sharma A. K, Kumar R, Kulshreshtha D, Gupta R, Chauhan P. K. S, Singh O. P. Vibrational Spectra of Aniline in Gas Phase: An Ab-Initio Study. Mat.Sci.Res.India;7(2). Available from: http://www.materialsciencejournal.org/?p=2404

Introduction

In recent years, considerable efforts have been devoted to understand the vibrational spectra of simple aromatic compounds. The role of aromatic amines is of basic importance in biology and chemical industry, particularly aniline and its derivatives are used in the production of dyes, pesticides and antioxidants.1-2

Some of the para-substituted derivatives of aniline are local anesthetics, and in these molecules the amino group plays an important role in the interaction with the corresponding receptor. Even in aniline, the amino group affects the planarity of the molecule and inclusion of an additional substituent group in aniline leads to further changes in the charge distribution in the molecule, and consequently affects the structural and vibrational parameters. Taking this into consideration it was thought worthwhile to calculate the vibrational frequencies of aniline at frist stage in order to establish the appropriate method along with basis set so that it would be applied to its other derivatives to see upto which extent the substituents affects the structrural and vibrational parameters.

Computational Detail

The entire calculations are performed at HF/6-31G(d) and Density functional Theory B3LYP/ 6-31G(d).All calculation in the present work were carried out in the Department of Physics, Paliwal Degree College Shikohabad on a Pentium IV PC using G03 and GAUSS VIEW 4.1 Version of abinitio quantum mechanical program.3-13 The optimized structural parameters are used in the vibrational frequency calculations at the HF and DFT to characterize all stationary points as minima. We have utilized the gradient corrected density functional theory (DFT)14 with the three parameters hybrid function (B3 for the exchange part) and Lee-Yang-Parr (LYP) Correlation Function, accepted as a cost effective approach for the computation of molecular structure, vibrational frequencies and energies of optimized structures. Vibrational frequency assignments are made with a high degree of accuracy.

Results and Discussion

Optimized Geometry

The optimized structure parameters of aniline calculated by HF/6-31G(d) and DFT B3LYP/6-31G(d ) along with same of their experimental values are listed in Table-1 and 2. The relative energies of aniline have also been calculated with different basis sets are presented in Table-3.

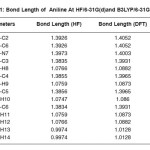
Table 1: Bond Length of Aniline At HF/6-31G(d)and B3LYP/6-31G(d)

Table 1:
Click on image to enlarge

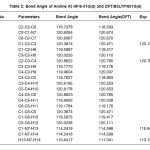
Table 2: Bond Angle of Aniline At HF/6-31G(d) and DFT/B3LYP/631G(d)

Table 2
Click on image to enlarge

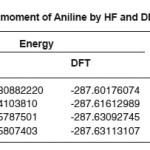
Table 3: Energy and Dipole moment of Aniline by HF and DFT with different basis sets

Table 3
Click on image to enlarge

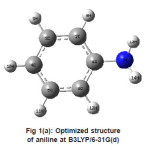
The optimized Hartree Fock C-N bond length (1.397Å) is found to be less than the experimental value while in DFT calculations the same (1.400 Å) is in good agreement with the experimental observation (1.402 Å). Similar results have also been found for the N-H bond length. On the other hand the the HF and DFT procedures give almost comparable magnitides for the bond angles. Table-3 shows that basis set which includes the polarized function has the most stable form of energy. In our study, vibrational frequencies calculated at HF/6-31G(d) and B3LYP/6-31G(d) level were scaled by 0.8929 and 0.9613, respectively. On the basis of the comparison between calculated and experimental results, assignment of fundamental modes were examined. The calculated frequncies are slightly lower than the experimental values for the majority of the normal modes. The infrared region of the electromagnetic spectrum extends from 14,000cm1 to 10cm-1. The region of most interest for chemical analysis is the mid-infrared region (4,000cm-1 to 400cm-1) which corresponds to changes in vibrational energies within the molecules. We have used HF and DFT optimized geometries as the starting point to calculate vibrational frequencies of Aniline. The number of atoms (N) in aniline are 14 therefore there are 13 stretching vibrations and 23 bending modes according to formula (N-1) and 3N-6-(N-1). The assignments for calculated frequencies of aniline at DFT/B3LYP/6-31G(d) are listed in Table-4. The optimized structures and IR spectrum of aniline calculated at DFT/B3LYP/6-31G(d) level are shown in fig. 1(a) and 1(b)

N-H2 Vibrations

The NH2 stretching frequencies of aniline has been accurately determined by Nakanaga et. al15 using the infrared depletion spectroscopy. For the aniline these authors observed two absorption bands of approximately equal infrared intensities, positioned at 3508 and 3422 cm-1. They assigned these bands to NH2 antisymmetric and symmetric stretching vibrations, respectively. As it is seen in Table-4 vibration 1 and 2 (V1andV2) are assigned to N-H2 stretching for B3LYP/6-31G(d) in the range of 3502 cm-1 and 3408 cm-1 for antisymmetric stretching and symmetric stretching, respectively, are in good agreement with the experimental values.

Table 4: Vibrational Frequencies of Aniline with HF/6-31G(d) and B3LYP/6-31G(d)

Table 4
Click on image to enlarge

Evan,16 in the IR spectroscopy studies of aniline in the gas phase and inert solvents, suggested that the two bands at 1115 and 1054 cm-1 involve deformation vibrations. Our calculations for aniline clearly indicates that (V18andV19) involves considerable contribution from the N-H rocking vibration. The calculated frequencies of these modes 1106 and 1037 cm-1 are in better agreement with the corresponding experimental values.

C-N Vibrations

The stretching vibration has been assigned at 1282 cm-1 in the IR spectrum of aniline by Gee et. al17. Our calculated frequency for this mode of vibration (V15) is found at 1265 cm-1 which is in good agreement with the experimental value. As is seen from Table-4 vibration (V25) also involves significant contribution from C-N stretching vibration. Michalska18 concluded that, in the IR spectrum of aniline, this vibration has been attributed to the band at 822cm-1 which is supported by our calculations. The C-N out of plane bending vibration is coupled with ring torsions and belongs mainly to the vibration V36, V32, V27. For the aniline the calculated frequencies of these vibration are 215, 489, and 734 cm-1, respectively are similar to experimental frequencies 217, 501 and 755 cm-1, respectively.

Phenyl Ring Vibrations

The vibration V21 and V19 in aniline can be described as ring in plane bending, which originates from the C-C stretching vibrations coupled with C-H in plane bending. These modes of vibrations were assigned 972 and 1037cm-1, respectively are comparable with experimental values for aniline in argon matrix.17 Both the modes of vibrations are very week in infra red spectra in as predicted by calculations and illustrated in fig1.The vibration V13 in the molecules can be described as the Kekule type vibration coupled with C-C stretching vibrations of the benzene ring. The B3LYP/6-31G(d) calculated frequencies of this mode 1324 cm-1 is in very good agreement with the experimental 1340 cm-1 reported by Evans.16

Figure 1(a): Optimized structure of aniline at B3LYP/6-31G(d)

Figure 1(a)
Click on image to enlarge

According to calculations, vibration V3 has been longest Raman scattering due to C-H stretching vibrations.The frequencies of these vibrations is in good agreement with experimental values. The calculated frequencies of modes V7 and V6 (3047 and 3048 cm-1), respectively, indicate that the corresponding anisymmetric stretching bands may overlap in vibrational spectra of aniline.

Figure 2

Figure 2
Click on image to enlarge

Conclusions

The HF/6-31G(d) and DFT/B3LYP/6-31G(d) calculations were performed for aniline molecule in gas phase. The calculated results show that predicted geometry can well reproduce the structural parameters. Scaled vibrational frequencies and their normal modes of vibration have been compared with experimental observations. It was found that DFT B3LYP/6-31G(d) method provides more satisfactory results as compared to HF/6-31G(d) because of the fact that Hartree Fock provides an inadequate treatment of the correlation between the motions of the electrons within a molecular systems especially that arising between electrons of opposite spin that remains uncorrelated. On the other hand the DFT approach is based upon a strategy of modeling electron correlation via general functionals of the electron density. The encouraging results so obtained lead us to apply the present procedure for other biologically, chemically and medicinally important derivatives of aniline in order to study the finer details affecting their structural and vibrational behaviour.

references

  1. Whysner J, Vera L & Williams G M, Pharmaco, Ther, 71: 107 (1996).
  2. Hohenberg P & Kohn W, Phy Rev, B 136: 864 (1964).
  3. Gaussian 03 Revision D.I., Frich M.J., Trucks G.W., Schlegel H.B.,Scruseria G.E., Robb M.A., Cheeseman J.R., Montgomery J. A., Jr., Verven T., Kudin K. N., Burant J.C., Millam J. M., Iyengar S. S., Tomasi J., Barone V., Mennucci B., Cossi M., Scalmani G., Rega N., Petersson G. A., Nakajima H., Hada M., Kitao O., Nakai H., Klene M., Li X., Knox J. E., Hratchtian H. P., Cross J. B., Bakken, V., Admo C., Jaramillo J., Comperts R., Stratmann, R. E.,Yazyev O., Austin A. J., Cammi R., Pomelli, C., Ochterski J. W., Ayala P.Y., Morokuma K., Voth G.A., Salvador P., Dannenberg J. J., Zakrzewski V. G., Dapprich S., Danniels A..D., Strain M.C., Farkas O ., Malick D.K., Rabuck A.D., Stefanov B. B., Liu G., Liashenko A.,Piskorz P., Komaromi I.,Martin R. L., Fox D. J., Keith T., Al- Laham M. A. Raghavachari K., Forcesman J. B., Ortiz J.. V., Cui Q., Cioslowski J., Peng C.Y., Nanayakkara A., Challacombe M., Gill P. M. W., Johnson B., Chen W.,Wrong M. W., Gonzalez C., and Pople J. A.,Gaussian Inc,Wallingford (2005).
  4. Hartree-Fock Frequencies: J.A. Pople, R.Krishnan H.B.Schlegel, D. DeFrees, J.S. Binkley, M.J. Frisch, R.F. Whiteside, R.F. Hout, and W.J. Hehre, Int. J.QuantumChem., Symp., 15: 269 (1981).
  5. P. Hohenberg and W. Kohn, Phys. Rev, 136: B864 (1964).
  6. W. Kohn and L. J. Sham, Phys., Rev. 140: A1133 (1965).
  7. The Challenge of d and f Electrons, Ed. D. R Salahub and M. C. Zerner (ACS,Washington D.C., 1989).
  8. 8. R. G. Parr and W. Yang, Density- functional theory of atoms and molecules (Oxford Univ. Press, Oxford, 1989).
  9. M. Head-Gordon, J. A. Pople, and M. J. Frisch, Chem.Phys Lett. 153: 503 (1988).
  10. M. J. Frisch, M. Head-Gordon, and J. A. Pople, Chem. Phys. Lett. 166: 275 (1990).
  11. M. J. Frisch, M. Head-Gordon, and J. A. Pople, Chem.Phys. Lett. 166: 281 (1990).
  12. R.H. Nobes, J.A. Pople, L. Ranom, N.C. Handy, P.J.Knowles, Chem Phys. Lett., 138: 481 (1987).
  13. H. B. Schlegel, J. Comp. Chem. 3: 214 (1982).
  14. DFT Frequencies and ZPE: M.W. Wong, Chem, Phys. Lett.,in Press. (1996).
  15. T. Nakanaga, F. Ito, J. Miyawaki, K. Sugawara, and H.Takeo, Chem. Phys. Lett. 261: 414 (1996).
  16. J. C. Evans, Specrochim. Acta 16: 428 (1960).
  17. Ch. Gee, S. Douin, C. Crepin, and Ph. Brechigiac, Chem. Phys.Lett. 338: 139 (2001).
  18. Piotr M. Wojciechowski, Wiktor Zierkiewicz, and Danuta Michalska. Journal of Chemical Phys. 118: 10900-10911(2003)
  19. Belgin BARDAKCI, Journal of Arts and Sciences SayiL7,Mayis, 13-19 (2007).
  20. Rakesh Kumar, A.K. Sharma, S.D.S. Chauhan, D. Kulshreshtha, R.Gupta, P.K.S. Chauhan, O.P. Singh, Material Science Research India 6(2): 551-558 (2009).
  21. A.K. Sharma, S.D.S. Chauhan, Rakesh Kumar, D. Kulshreshtha, R.Gupta, P.K.S. Chauhan, O.P. Singh, Material Science Research, India 6(2): 423-430 (2009).
  22. A .A. El-Barbary, M.M. El-Nahass, M. A .Kamel, M.A.M. El-Mansy. Journal of Applied Sciences Research, 5(11): 1977-1987 (2009).
Share Button

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

Designed by: Designtohost
Copyright © 2024 MSRI