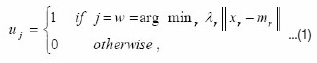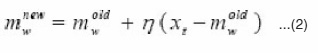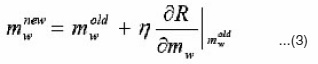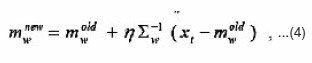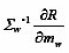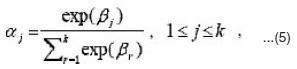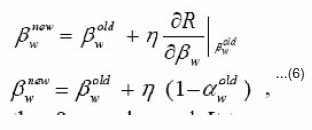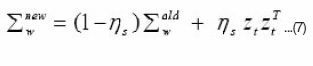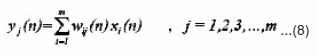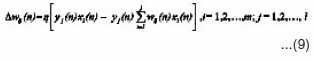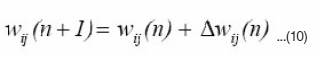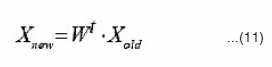Wael M. Khedr and Qamar A. Awad
Mathematical Department, Faculty of Science, Zagazig University (Egypt).
DOI : http://dx.doi.org/10.13005/msri/080101
Article Publishing History
Article Received on : 14 Jan 2011
Article Accepted on : 18 Feb 2011
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:
In this paper, we propose adaptive K-means algorithm upon the principal component analysis PCA feature extraction to pattern recognition by using a neural network model. Adaptive k-means to discriminate among objects belonging to different groups based upon the principal component analysis PCA implemented for statistical feature extraction. The features extracted by PCA consistently reduction dimensional algorithm, thus demonstrating that the suite of structure detectors effectively performs generalized feature extraction. The classification accuracies achieved using feature learning process of back propagation neural network . A comparison of the proposed adaptive and previous non-adaptive ensemble is the primary goal of the experiments. We evaluated the performance of the clustering ensemble algorithms by matching the detected and the known partitions of the iris dataset. The best possible matching of clusters provides a measure of performance expressed as the misassignment rate.
KEYWORDS:
Adaptive K-means algorithm; PCA; Neural network; Backpropagation algorithm
Copy the following to cite this article:
Khedr W. M, Awad Q. A. Neural Network and Adaptive Feature Extraction Technique for Pattern Recognition. Mat.Sci.Res.India;8(1)
|
Copy the following to cite this URL:
Khedr W. M, Awad Q. A. Neural Network and Adaptive Feature Extraction Technique for Pattern Recognition. Mat.Sci.Res.India;8(1). Available from: http://www.materialsciencejournal.org/?p=2453
|
Introduction
The design of a recognition system requires careful attention to the following issues: definition of pattern classes, pattern representation, feature extraction, cluster analysis, classifier design and learning, selection of training and test samples, and performance evaluation.
Interest in the area of pattern recognition has been renewed recently due to emerging applications which are not only challenging but also computationally more demanding. These applications include data mining, document classification, financial forecasting, organization and retrieval of multimedia databases, and biometrics (personal identification based on various physical attributes such as face and fingerprints).
Clustering analysis is a fundamental but important tool in statistical data analysis. In the past, the clustering techniques have been widely applied in a variety of scientific areas such as pattern recognition,6 information retrieval, microbiology analysis, and so forth. In the literature, the k-means2 is a typical clustering algorithm, which aims to partition N inputs (also called data points interchangeably).
The most commonly used family of neural networks for pattern classification tasks4 is the feed- forward network, which includes multilayer perceptron and Radial-Basis Function (RBF) networks. These networks are organized into layers and have unidirectional connections between the layers. Another popular network is the Self- Organizing Map (SOM), or Kohonen-Network,5 which is mainly used for data clustering and feature mapping. The learning process involves updating network architecture and connection weights so that a network can efficiently perform a specific classification/clustering task. The increasing popularity of neural network models to solve pattern recognition problems has been primarily due to their seemingly low dependence on domain-specific knowledge.
Adaptive K-Means Cluster Algorithm
The adaptive k-means algorithm is built on Kullback scheme,7 its details steps as follows:
Step 1
We implement this step by using Frequency Sensitive Competitive Learning1 because they can achieve the goal as long as the number of seed points is not less than the exact number K of clusters. Here, we suppose the number of clusters is k≥k*, and randomly initialize the k seed points m1 , m2 , . . . , mk in the input data set.
Step 1.1
Randomly pick up a data point xt from the input data set, and for j = 1, 2, . . . , k, let
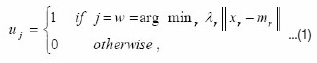
where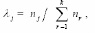 
and nr is the cumulative number of the occurrences of ur = 1.
Step 1.2
Update the winning seed point mw only by
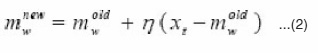
Steps 1.1 and 1.2 are repeatedly implemented until the k series of uj for j = 1, 2, . . . , k remain unchanged for all xt s. Then go to Step 2.
In the above, we have not included the input covariance information in Eqs. (2) and (3) because this step merely aims to allocate the seed points into some desired regions as stated before, rather than making a precise value estimate of them. Hence, we can simply ignore the covariance information to save the considerable computing cost in the estimate of a covariance matrix.
Step 2
Initialize αj = 1/k for j = 1, 2, . . . , k, and let Σj be the covariance matrix of those data points with uj = 1. In the following, we adaptively learn αj s, mj s and Σj s
Step 2.1
Given a data point xt, calculate I( j ē xt ) s by Eq. (1).
Step 2.2
Update the winning seed point mw only by
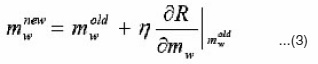
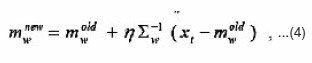
or simply by Eq.(3)without considering Σw-1. In the latter, we actually update mw alongthe
direction of
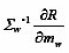
that forms an acute angle angle to the gradient-descent direction. Further, we have to update the parameters αj s and Σw. through a constrained optimization algorithm in view of the constraints on aj s in Eq. (5). Alternatively, we here let
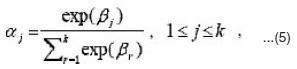
where the constraints of aj s are automatically satisfied, but the new variables bj s are totally free. Consequently, instead of bj s, we can learn bnew only by
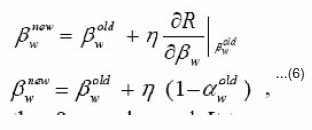
with the other bjs unchanged. It turns out that aw is exclusively increased while the other ajs arepenalized,i.e.,their values are decreased.Here, please note that, although bjs are gradually convergent, Eq. (6) always makes the updatingof b increase without an upper bound upon the fact the aw is always smaller than 1 in general. To avoid this undesirable situation, one feasible way is to subtract a positive constant cb from all bjs when the largest one of bjs reaches a prespecified positive threshol dvalue.
As for Sw , we update it with a small step size
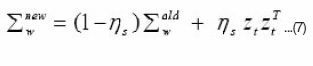
where
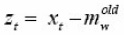
and ηs is a small positive learning rate, e.g. ηs = 0.1η. In general, the learning of a covariance matrix is more sensitive to the learning step size than the other parameters.
The simple K-means partitional clustering algorithm described above is computationally efficient and gives surprisingly good results if the clusters are compact, hyper spherical in shape and well-separated in the feature space. If the Mahalanobis distance is used in defining the squared error in (3), then the algorithm is even able to detect hyper ellipsoidal shaped clusters.
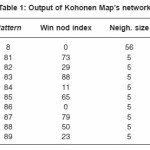
Table 1: Output of Kohonen Map’s network
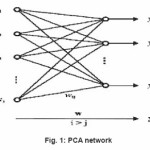
Fig. 1: PCA network
Fig. 2: Handwritten digits numbers from 0 to 9, image of(28×28)
Fig. 3: Digits numbers from 0 to 9, image of 7×7
Fig. 4: Reconstruction Digits from PCA
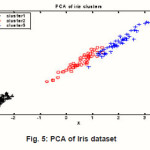
Fig. 5: PCA of Iris dataset
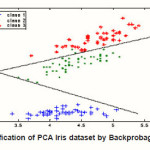
Fig. 6: Classification of PCA Iris dataset by Backprobagation network
PCA Feature Extraction by Hebbian Algorithm
The principal component analysis (PCA) is a Multivariate Statistical Process Control (MSPC) methods. Feature extraction methods determine an appropriate subspace of dimensionality m (either in a linear or a nonlinear way) in the original feature space of dimensionality n, such that m is less than n. Linear transforms, such as principal component analysis, factor analysis, linear discriminant analysis, and projection pursuit have been widely used in pattern recognition for feature extraction and dimensionality reduction. Principal components can be extracted using single-layer feed-forward neural networks.8
Hebbian Learning process
There is a close correspondence between the behavior of self-organizing neural networks and the statistical method of principal component analysis. In fact, a self-organizing, fully interconnected 2-layer network with i inputs and j outputs (with i > j) can be used to extract the first j principal components from the input vector, thus reducing the size of the input vector by j-i elements as shown in fig.(1). With j=1, such a network acts as a maximum eigenf ilter by extracting the first principal component from the input vector. The algorithm used to train the network is based on Hebb’s postulate of learning.
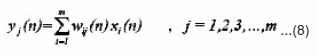
Hebbian Learning process by eq.(9)
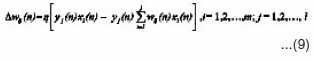
Here n denotes the number of training samples, and the learning rate. The attentive reader will notice that the unconstrained use of this learning algorithm would drive to infinity because the weight would always grow but never be decreased. In order to overcome this problem, some sort of normalization or saturation factor needs to be introduced. A proportional decrease of wi by a normalization term introduces competition among the synapses, which, as a principle of self- organization, is essential for the stabilization of the learning process.
The adjusted weight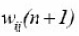 
is calculated as
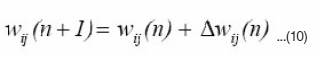
Reconstruction pattern from Hebb network by eq(11)
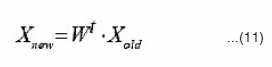
In general, the algorithm converges very quickly. There is, however, one serious problem: errors in the input vector may cause some weights to break through the constraint mechanism and grow to infinity, which as a result destroys the PCA filter. The implementation should throw an exception when a particular weight grows above an appropriate upperlimit.
Application Of PCA On Handwritten
We applied the PCA by Hebbian on a handwritten digits numbers from 0 to 9, which represented by image of (28×28) pixels as shown in figure (). We have been applied a Kohonen ‘s map network to recognition theses pattern. The result of recognition is shown in table(1)
Application of Adaptive K-Means and PCA Algorithm On Iris Dataset
A data set with 150 random samples with nine size dimensional space of flowers from their is species setosa, versicolor, and virginica collected by Anderson (1935). From each species there are 50 observations for sepal length, sepal width,petal length, and petal width in cm.
We applied adaptive K-means algorithm to classify 150 samples dataset into three clusters and applied PCA algorithm to reduce the dimensional into two size. The classification accuracies achieved using the half of dataset features to learning process of back propagation neural network, the result of classification is shown as in Fig.
References
- Ahalt, S.C., Krishnamurty, A.K., Chen, P., Melton, D.E., Competitive learning algorithms for vector quantization. Neural Networks 3: 277-291 (1990).
CrossRef
- MacQueen, J.B., Some methods for classification and analysis of multivariate observations. In: Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability, 1. University of California Press, Berkeley, CA, pp. 281-297 (1967).
- C. Y. Suen and J. Tan, “Analysis of errors of handwritten digits made by a multitude of classifiers,” Pattern Recognition Letters, 26: 369-379 (2005).
CrossRef
- A.K. Jain, J. Mao, and K.M. Mohiuddin, Artificial Neural Networks: A Tutorial, Computer, pp. 31-44, Mar. 1996.
CrossRef
- T. Kohonen, Self-Organizing Maps. Springer Series in Information Sciences, 30, Berlin (1995).
CrossRef
- Hareven, M., Brailovsky, V.L., Probabilistic validation approach for clustering. Pattern Recognition Lett. 16: 1189-1196 (1995).
CrossRef
- Xu, L., 1995. Ying-Yang Machine: A Bayesian–Kullback scheme for unified learning and new results on vector.
- Sanger, 1989; Rubner and Tavan, 1989; Oja, 1989; Diamantaras and Kung (1996).
- A. L.C. Barczak, M. J. Johnson, C. H. Messom, ‘Revisiting Moment Invariants: Rapid Feature Extraction and Classification for Handwritten Digits’, Proceedings of Image and Vision Computing New Zealand 2007, pp. 137–142, Hamilton, New Zealand, December 2007.
- A. L. C. Barczak and M. J. Johnson, “A new rapid feature extraction method for computer vision based on moments,” in International Conference in Image and Vision Computing NZ (IVCNZ 2006), Auckland, NZ, 395–400 (2006).
- M. Girolami. Mercer kernel based clustering in feature space. IEEE Transactions on Neural Networks, 13(4):669–688 (2002).
CrossRef
This work is licensed under a Creative Commons Attribution 4.0 International License.
Material Science Research India An International Peer Reviewed Research Journal
PDF Downloads:
877
Open
Access -
