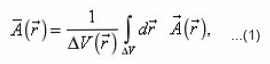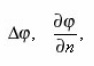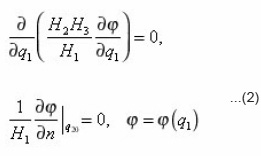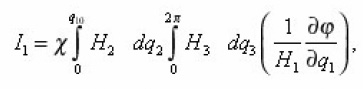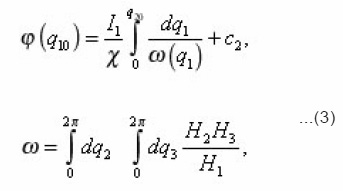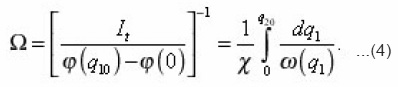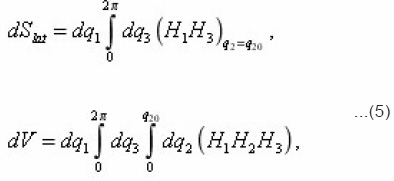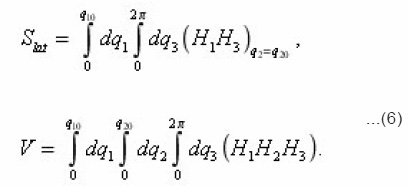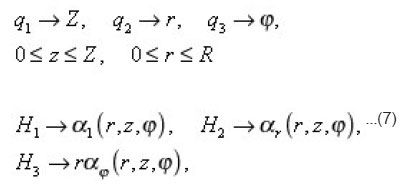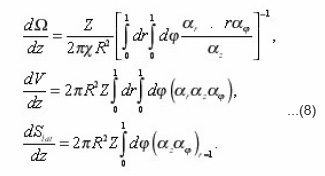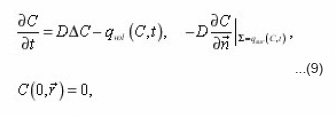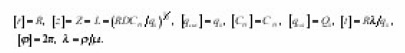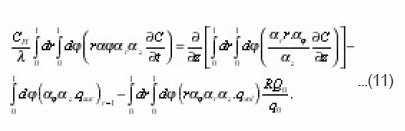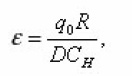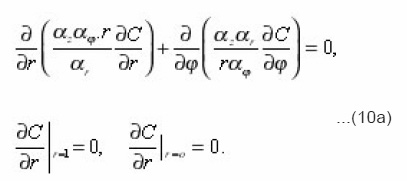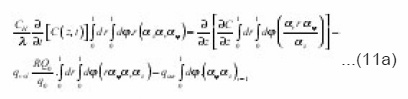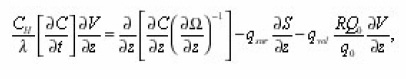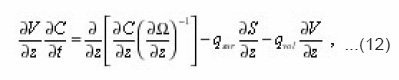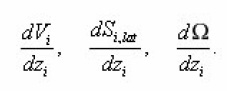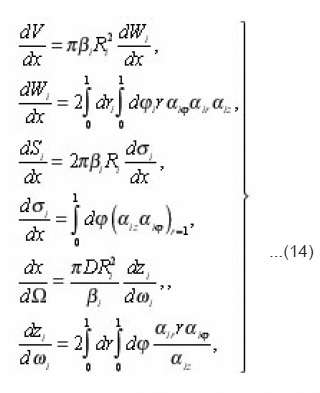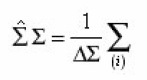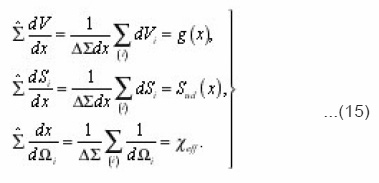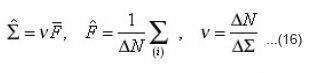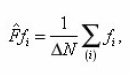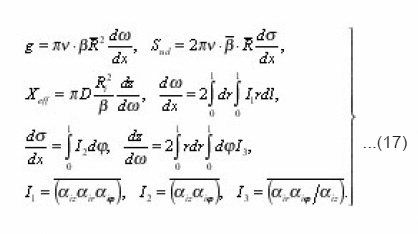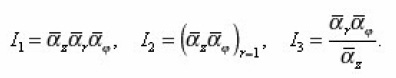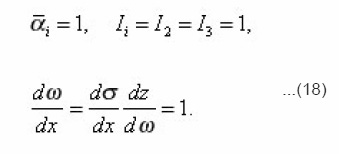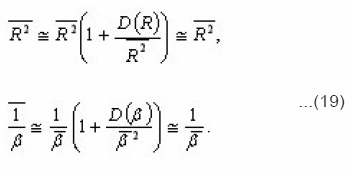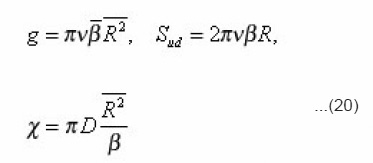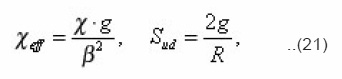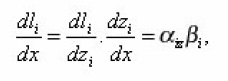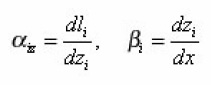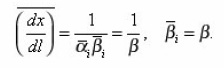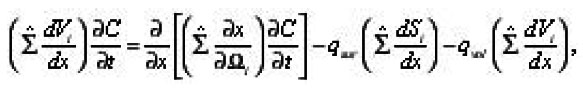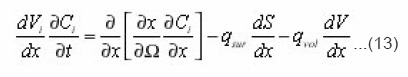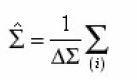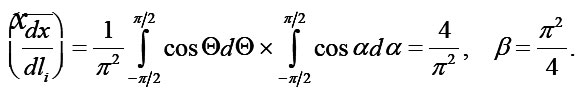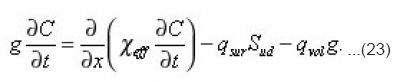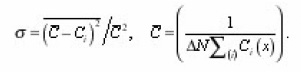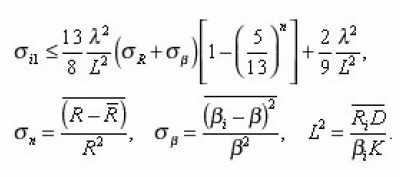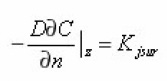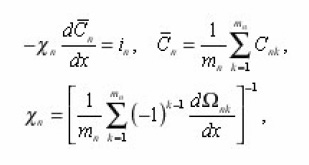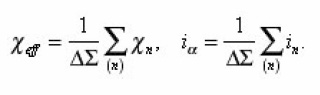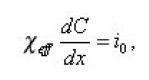PDF Downloads: 819

Transport Processes in Environments with Irregular Structure

Saif A. Mouhammad

Department of Physics, University College - Um Alqura University, Makkah, Saudi Arabia.

DOI : http://dx.doi.org/10.13005/msri/080102

Article Publishing History
Article Received on : 10 May 2011
Article Accepted on : 12 Jun 2011
Article Published :
Plagiarism Check: No

Article Metrics

ABSTRACT:

In this work we consider a principally new statistical approach to the theory of processes of transport in a two-phase condensed environment with randomly distributed non-uniform surface structure. Taking this approach as a base, we considered diffusion in a chaotic porous environment. Such a structure is described with the aid of a curvilinear orthogonal coordinates system natural for geometrical porous surface. The method of averaging the diffusion equation is developed. The equations for average diffused concentration in a porous surface of a solution of ionic components are obtained. These equations take into account the local characteristics of the structure of the environment. In general, this approach is applicable to other equations describing the transport of substance, charge and electromagnetic field in the environment with random interior.

KEYWORDS: Transport process theory; Environment; Irregular structures

Copy the following to cite this article:

Mouhammad S. A. Transport Processes in Environments with Irregular Structure. Mat.Sci.Res.India;8(1)

Copy the following to cite this URL:

Mouhammad S. A. Transport Processes in Environments with Irregular Structure. Mat.Sci.Res.India;8(1). Available from: http://www.materialsciencejournal.org/?p=2456

Introduction

It is known that the difficulty of solution of the problem about the transport of substance and charge in a porous environment is caused by the presence of the complex interphase boundary Σ of pore space, which for a chaotic environment is random. In the most realistic case, the very notion of the pores is not defined, which is intuitive. Therefore, in applied researches resort to the simplified representations, replacing real porous by system modeling. Modeling is achieved by a precise definition of the pores and becomes necessary to solving the relationship between such integral quantities as porosity g, specific internal surface S, the average pore radius R, and etc. However, in this case arbitrary assumptions are In this paper, a proposed method for calculating the above- indicated quantities for an arbitrary environment, principally different from the commonly used. It allows us to consider the geometry of the pore space and to investigate transport processes in it without the modeling approaches. The structure of space is assumed to be chaotic, i.e., random. This method is based on the use of an apparatus of orthogonal curvilinear cylindrical coordinates, moreover in each i pore is determined by its eigenvalue cylindrical curvilinear coordinates r_i, z_i, φ_i.

We define at first the average value

of some local quantities

by ΔV, volume sufficiently small relative to the size of the environment, but large in comparison with the characteristic scale R of surface change

vol8_no1_tra_sai_eq1

Where

–

the local radius-vector

corresponds to the center

The average

can be identified with the observable quantities (since measurement inevitably accompanies averaging) and simultaneously integrated characteristics of environment and processes (at presence of processes, random in time of eq. (1) must be averaged and for some time interval dt, exceeded the period of temporary time fluctuations, since with the reproducible measurements of the fluctuations also averaged). The problem of transport theory in porous environments consists in averagings of the true (microscopic) equations for local

and the solution of the equations obtained in this way for those are observed

Thus equivalence between obtained average and true integrated properties of system is automatically observed.

The mathematical apparatus, which allows describing the e, in this paper, is based on the choice of appropriate systems of orthogonal curvilinear coordinates, which is naturalized for the pore geometry. With this purpose, we consider the flow of some physical quantity

(for determining electric field) in the liquid phase, which does not contain volumetric sources. It is obvious that, the current lines and its equipotential (related to the solution of Laplace equation

are determined by the geometry of the pore space Ω and the additional conditions on its boundary

If the surface Σ is non- conducting, then the current lines will be located along Σ and its equipotential is orthogonal to it. Due to randomness of the structure, some equipotential necessarily tangent to the walls Σ. Points (or curved) of contact of tangency will determine simultaneously the places of the branching of current. Such equipotentials will divide entirely the pore space Ω into the separate elements, in each of which branch point will be absent. single- valued regions Ωi in general case are simply individual pores.

In each i pore let us consider – instead of orthogonal curvilinear coordinate- a system of lines q₁, coinciding with the current lines, and surfaces, coinciding with the equipotentials. On the surfaces, we introduce a q₂lines, orthogonal to the walls of the pores, and lines q₃, closed and orthogonal to q₂ lines. Reference index and intervals change of coordinates q₁₂₃we will define them as follows: 1) q₁is counted from initial, i.e. passing through branching point of equipotential plane. Then, final equipotential corresponds to maximum value q₁ = q₁₀ ;2) is counted from an axial line, unique in each pore. The maximum value of q₁ = q₁₀ is achieved at the wall of the pore; the coordinate is cyclic, measured in radians

and the beginning of its index is arbitrary..

Coordinates q₁, q₂, q₃for each of the pore are Eigenvalue. Each one q should provide with an index , for simplicity can be omitted. With their aid we can get an expression for the conductivity and other characteristics of individual pores.

Actually, the potential j, is defined by the boundary-value problem

scheme3

vol8_no1_tra_sai_eq2

Next, we use the expression of the total current through the pore, equal to

scheme4

Hence, taking into account

we have

vol8_no1_tra_sai_eq3

The resistance of pores

vol8_no1_tra_sai_eq4

lateral surface area

and volume

vol8_no1_tra_sai_eq5

vol8_no1_tra_sai_eq6

Cyclicity

allows to consider

as the generalized cylindrical coordinates, and below it is convenient to redesignate:

vol8_no2_tra_sai_eq_7

r ,z are measured in the arbitrary units of the length (which correspond to the limiting values R,Z and dimensionless coefficients). Elementary

arcs Using this, it is possible to connect
with the average section

of pores, not depend on z. Since for the rectilinear cylindrical coordinates

that the difference from unit q_ir=q₁ assigns the measure for the deviation of generalized coordinates

from the usual cylindrical.

on the transition

the characteristics of individual pore (4)-(6) after utilizing dimensionless coordinates with the aid of the scales

will be transformed to the form

equation 8

The method of eigenvalue coordinates of pores allows to obtain the transport equations in a single pore, expressing its coefficients through the local parameters (8). Let us for this purpose consider, for example, the diffusion of the components of the solution with the concentration in the liquid pores, determined in the general case by boundary-value problem

equation 9

Where q_vol , q_sur – the density of the volumetric and surface sources,

-normal to the interphase boundary Σ. The equation (9) is now to carry on an individual i pore, assuming Σ its lateral surface. In Σ its eigenvalue coordinates r, z, φ, are made dimensionless using the scale

equation z

The problem (9) is written in the form of (index i, r, z, φ and other variables, are omitted for brevity, it is assumed):

equation 10

The conjugation conditions at the border with neighboring pores is expected to be met. If all the terms are multiplied by a factor

integrated by the coordinates and take into account the boundary conditions , then (10) is reduced to use in the future as an integral form

equation 11

In the equation (10), the parameter ε is equal to the ratio of the characteristic scales of absorption flow q₀ on the boundary surface and diffusion,

equation A

But L is interpreted as the depth of penetration of diffusion into the volume of the environment. Since it is assumed that the substance is transferred through entire pore space, then and are small q₀ and ε respectively

(Otherwise, the limit within one pore, absorption almost complete). Therefore in (10) it is possible to use a perturbation theory and to represent C ( r,z,φ,0)

with a series in powers of small parameter . Then in the zero by approximation, on the basis of (10),

we have

Physically necessary solution of the equation (10 a) is an arbitrary function C = C ( t,z) of time and eigenvalues coordinate z. It simultaneously satisfies the equation (11) which is due to the independence of C on r and Φ is simplified:

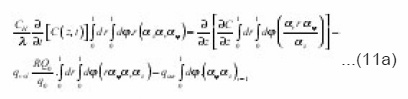
equation 11a

Coefficients (11a) coincide with the integrals (8), and if we make

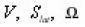
dimensionless with the aid of the scales

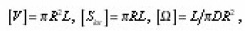
then (11) is led to the formula:

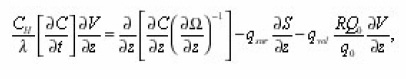
equation F

or in the dimensional form:

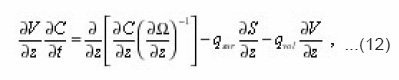
equation 12

Thus, it is possible to establish, that the equation (12), which expresses the balance of substance in the volume dv of a certain pore, connected the transport process with its local characteristics. This gives the possibility to consider the problems, complicated by the presence of mobile interphase boundary and to express the effective transport coefficients through the integral characteristics of environment. Let’s proceed with expressions (8) for local parameters

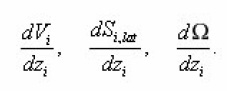
equation G

Preliminarily let us pass, using determination of sinuosity

equation 13

from z to the homogeneous coordinate x , on which all depend macroscopical, i.e. the averaged values. In a case of plane-parallel medium considered below the axis is perpendicular to its surface and

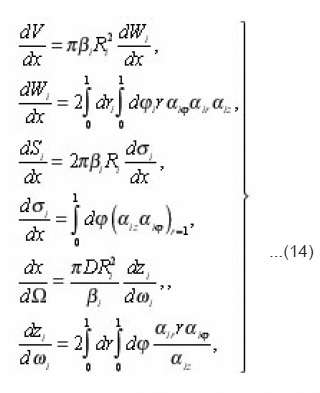
equation 14

Where z_i, x – dimensional, and therefore Z is absent.

For the calculation g, s_ud, x_efit isnecessary to average (14) with the aid of the rule

(1), and since V_i, S_iare volume and surface of pores, then as a result of their averagings we will obtain g and s_udAs the volume of averaging Δv = ΔΣ. Δx let us select infinitely thin layer ( x, x+ Δx ) with the area of base ΔΣ and will act on the equation (2) by the operator

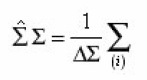
equation H

Summation over all N(x) pores of the layer. Then on the left side we obtain:

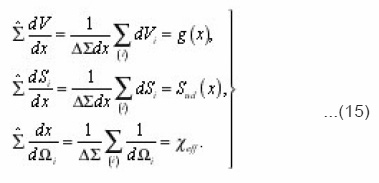
equation 15

To the right in (14) it is convenient to represent

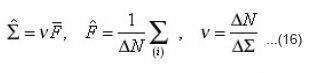
equation 16

It is obvious, that is equal the density of pores, which intersect layer ( x, x + dx ) At

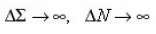
formula

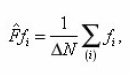
equation J

determines mean-static

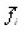
on the infinite ensemble of pores of section. From this point of view, by the force of limitation ΔΣ use (16) gives, strictly speaking, an average on a certain sample ΔN from this ensemble, and the density can fluctuate. However, since the probability of deviations from f is proportional 1/ΔN, and

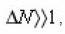
then the below noted difference is ignored. From (14), (15) we find

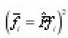
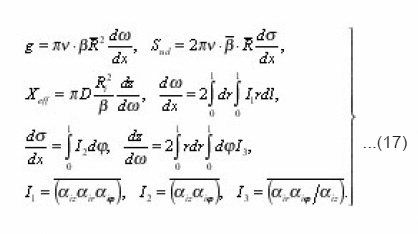
equation 17

Calculating l₁₂₃, taking into account that

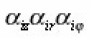
they characterize the curvatures of arcs in the generalized coordinate system relative to the appropriate arcs of the usual cylindrical system (where α_z=α_r=α_φ=1).

In the chaotic porous space, these curvatures are independent for different directions, so that

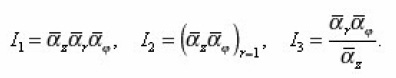
equation M

At the same time, as a result of uniformity of medium along the section ΔΣ and complete chaos in the geometry of pores, any deviations from one are equally probable and consequently

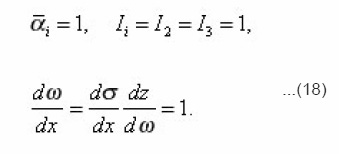
Equation 18

If dispersions D(R) and D(β) are small, then

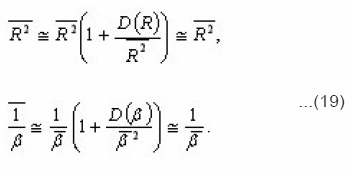
equation 19

νdl_Dx_z, dl _r , dl_ϕ

And by the force of (17)-(19), we obtain

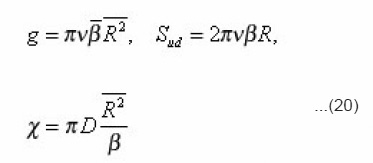
equation 20

Thus, five integral characteristics g, sud, xeff, v, β, R , are bound by three relations (20). From them, in particular, follow the equalities

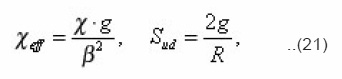
equation 21

which in the general case of arbitrary environment were not obtained. For the problems of electrical conductivity the diffusion coefficient in (20) is substituted by the coefficient of electrical conductivity χ. Sinuosity β is found from the determination of arc length dl_i=α_izdz_i..

Actually, since

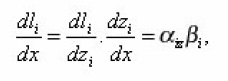
equation N

Where

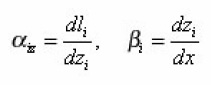
equation O

Then, averaging this equation over an ensemble of pores, we have

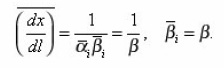
equation P

Since

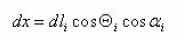
(Where-

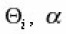
the Directing angles of the arcs dl_i) and averagings over the ensemble and all orientations of arcs relative to axis are equivalent, then

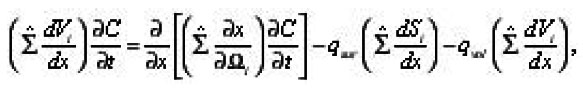
equation 22

With the aid of that used above for calculating (20) the procedure it is possible to average the equation of diffusion in the separate pore. In the beginning in (12) we will pass from eigenvalues to the homogeneous coordinate.Then we obtain taking into account (13)

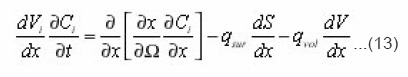
equation 13A

On both parts of (20), let us act by the operator of summation

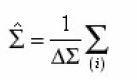
equation S

and let us consider that the concentration C_i(x) must weakly depend on index i, i.e., the number of pore in the section ΔΣ. This is a consequence of connectivity and cross-pore space. Owing to the fulfillment of conditions for conjugation in the points of small intersections of the root-mean-square spread σ of values C_i(x), caused by difference in the geometry of the pores of layer (x,x+dx) and their previous branchings (see below). Therefore all values, connected with C_i(x) it is possible to carry out from the summation sign and then from (22) we find

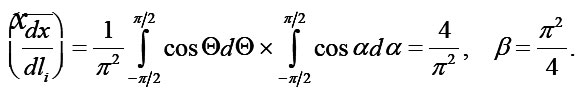
equation T

Where q_sur and q_volhave already the sense of averages by volume ΔΣdx density of sources. Hence, taking into account (15) we finally obtain the required equation for the averages

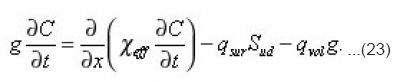
equation 23

The presented method makes it possible to derive in the subsequently equations, analogous (23), in the case of mobile interphase boundary. The diffusion of the components of the solution in the porous medium, accompanied by their crystallization on the pore walls, can serve as its example.

Let us return to evaluation quantity

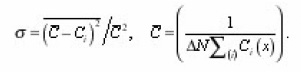
equation U

For this it is expedient to consider the simplest model, which assumes all intersections with those (!!!!) located in the planes x_n = λn. where n=1,2,3…,β₀λ- the average length of the pores. Furthermore, let us accept their radii R_i sinuosity β_i as that being independent of x, and the probability of branching and confluence (merging) in each plane equal. Then, using expressions forthe concentrations at the nodal points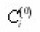

which appear from equations of diffusion, also of conjugating conditions, it is possible to show that

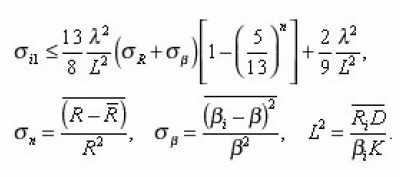
equation V

Summing up is here produced with the aid of

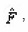
On the Boundary x=0 , (corresponding n=0) ) all concentrations

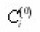
are equal and, consequently

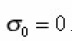
The parameter in the expression defines the flow to the surface of the pore

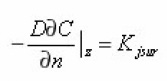
equation Z

And the depth of penetration of diffusion into the porous environment is assigned.

And since it is great in comparison with the length of pore

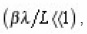
then σ is small and, therefore, C_i is weakly depends on i.Further let us pause in greater detail at the determination of sinuosity β(x). Formula (13) assumes that, β – the single-valued function of homogeneous coordinate x . However, this condition is disrupted, if a certain part of the pores had turning points, so that they intersect layer (x, x +dx) several times in opposite directions (in the chaotic pore space the probability of this it is certain, it is small). Then procedure presented above necessary to generalize, since the flow of diffusion current for-branching pore corresponds to the series, but not parallel connection of its elements of those belonging to the allocated layer (x, x +dx) and this influences the calculation of

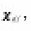
moreover sinuosity

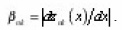
Considering for simplicity the case of absence the sources, it is easy to show that the average for all-branches of the pore concentration value satisfies the equation

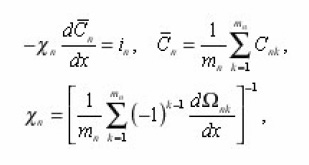
equation A3

Where- the current through the pore. According to its meaning is the conductivity of the layer of unit thickness, containing a single pore. Therefore it is clear that effective conductivity

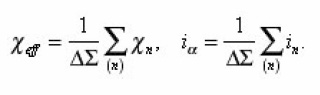
equation A4

Acting by the operator of summing up S to both parts of (12) again, we come to the homogeneous equation

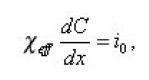
equation A5

analogous (11). Summarizing the state that the above obtained relations connecting the effective transport coefficients with the structure of an arbitrary porous environment. A general method is developed, which allows to obtain in different cases the homogeneous transport equation.

References

Color R., and others. Optical holography.V. 1. – Moscow: MIR. – 1973.
Komotskii V. A., Black T. D. Analysis and application of stationary reference grating method for optical detection of surface acoustic waves // J. Appl. Phys.- V. 52 (January 1981).
CrossRef
Kaufman M., Seidman A. Handbook of electronics calculation for engineers and technicians. McGraw-Hill, New York, 1988 ISBN 5-283-02512-8 (V.2, Russ.) ISBN 5- 283-02506-3 (Russ.) ISBN 0-07-033528-1 (Eng.).
Oliner A., edited by. Surface acoustic waves.- Moscow: MIR.- 1981.
Komotskii V. A., Application of methods of three-dimensional frequency response analysis for the solution of some problems of coherent optics.- Moscow: RFU.-1994.
Bessonov A. F., and others. Measurement of the phase distributions of surface acoustic waves by the method of optical sounding with the supporting diffraction of the lattice // Autometry.5 (1982).
Deryugin l. N., and others. Practical realization of the phase measurements of surface acoustic waves at optical sounding with the supporting diffraction of the lattice // Autometry. 3 (1988).
Bessonov A. F., and others. Optical sounding of surface acoustic waves in the presence of stationary periodic lattice // Optics and spectroscopy. V. 49(1980).
Bessonov A. F., and others. Interaction analysis of light wave with the system of the three-dimensional diverse periodic structures during the optical sounding of surface acoustic waves // Optics and spectroscopy.- V. 56(1984).
Komotskii V. A., et al. An optical setup for measuring amplitude and phase distributions of surface acoustic waves // Instrument and experimental techniques. V. 41(1998).
Kaschenko N. M., Komotskii V. A. On November 23-25, 1999. – The measurement of rectangular periodic structures with the aid of the laser sounding. – the 6th All-Russian scientific and technical conference “State and the problem of the measurements” Theses of reports, the second part. Moscow.
Komotskii V. A. On May 19 to 22, 1998. – The improvement of the optical method of determining the depth of the periodic structures.- 34 scientific conference of the faculty of physical-mathematical and natural sciences. Moscow: RFU.- Theses of reports, physical sections, the publishing house of the Russian friendship university, p.29 (1998).
Kaschenko N. M., Komotskii V. A. On May 24 to 28, 1999. – measurement of the depth of supporting diffraction of lattices at a deviation of the form from meander.- Theses of reports, physical sections. Moscow: RFU.
Komotskii V. A. Characteristic and the possibilities of a method of the optical sounding of surface acoustic waves with the use of supporting diffraction lattices // Bulletin RFU.- V. 1 (1993).
Kaschenko N. M., Komotskii V. A. Phase measurements of wave fields of surface acoustic waves by a method of optical sounding with the use of supporting diffraction lattices // Bulletin RFU.- V. 1 (1998).