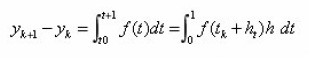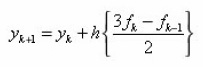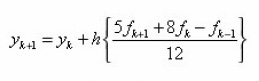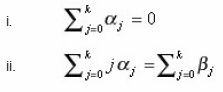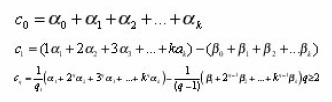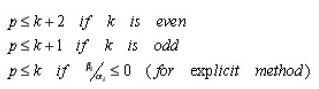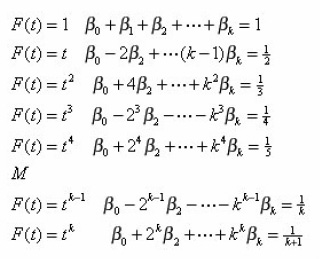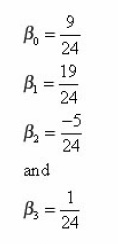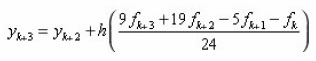Views 
   PDF Download PDF Downloads: 854

 Open Access -   Download full article: 

A Class of Adams-Like Implicit Collocation Methods of Higher Orders for the Solutions of Initial Value Problems

J. O. Fatokun1*, Tsaku Nuhu1 and I. K. O Ajibola2

1Department of Mathematical Sciences.Nasarawa State University.P.M.B.1022, Keffi, Nigeria. 

2Department of Mathematics and Statistics, Polytechnic of Namibia, Windhoek, Namibia.

DOI : http://dx.doi.org/10.13005/msri/080107

Article Publishing History
Article Received on : 10 May 2011
Article Accepted on : 12 Jul 2011
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:

The focus of this research work is the derivation of a class of Adams-like collocation multistep methods of orders not exceeding p=9. Numerical quadrature rule is used to derive steps k= 3,...,8 of the Adams methods. Convergence of each formula derived is established in this paper. As a numerical experiment, the step six pair of the Adams method so derived was used as predictor-corrector pair to solve a non-stiff initial value problem. The absolute errors show an accuracy of o(h7).

KEYWORDS: Adams methods; Numerical quadrature; Stability; Order of accuracy; predictor-corrector methods

Copy the following to cite this article:

Fatokun J. O, Nuhu T, Ajibola I. K. O. A Class of Adams-Like Implicit Collocation Methods of Higher Orders for the Solutions of Initial Value Problems. Mat.Sci.Res.India;8(1)

Copy the following to cite this URL:

Fatokun J. O, Nuhu T, Ajibola I. K. O. A Class of Adams-Like Implicit Collocation Methods of Higher Orders for the Solutions of Initial Value Problems. Mat.Sci.Res.India;8(1). Available from: http://www.materialsciencejournal.org/?p=2472

Introduction

The Adams methods constitute an important class of multistep method for the numerical solutions of ordinary differential equations. In contrast to one-step methods, multistep methods increase efficiency by using the information from several previous solution approximations.

These methods were introduced by J.Couch Adams (1883) for solving problems of capillary action due to Francis Bashforth. Bashforth published his numerical theory and Adams’ numerical method (Goldstine, 1977). They are based on the following idea:

Suppose that the solution y(t) is in fact a polynomial and the function f (t, y) has no explicit dependence on y, then it follows that

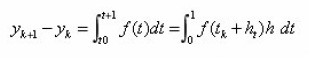
equation1

We seek the values of the coefficients βj so that the corresponding formula has the maximum possible degree of precision. (Note here that the corresponding numerical integration rule would use points from outside the range of integration). A ready example in literature is the popular two-step order two explicit method given as

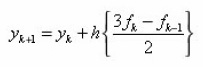
equation 2

The Adams Moulton methods are solely due to John Couch Adams, like the Adams Bashforth methods. The name of Forest Ray Moulton became associated with the method because he realised that they could be used in tandem with the Adams Bashforth methods as a predictor- corrector pair (Moulton 1926). The two-step order three implicit method is given as.

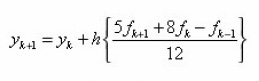
equation 3

Theorem Due Dahlquist

A linear multistep

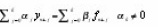
equation 4

0 method is said to be convergent if it is consistent and zero stable.

A linear multistep method is consistent if it satisfies the conditions below

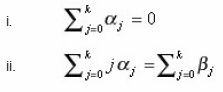
equation 5

A linear multistep method is said to be zero stable if the roots of the characteristic polynomial

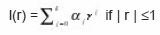
equation 6

and each root is distinct

Order of Accuracy of Linear Multistep Methods

Equation (2) is said to have order of accuracy p if p is the largest positive integer such that for any sufficiently smooth curve in the rectangular domain D of the first order initial value problem (Equation 1). There exist constants k and h0 such that for |Tn| ≤ khp for 0<h<, for any k+1 points 

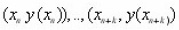
equation 7

on the solution curve. We can thus deduce that the method (equation 2) is of order of accuracy p if and only if

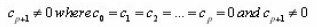
equation 8

in this case is the error constant.

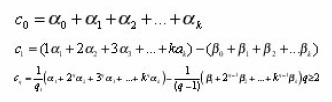
equation 9

Highest Attainable Order of Stable Multistep Methods

It is a natural task to investigate the stability of the multistep methods with highest possible order. Counting the order conditions shows that for order p the parameters of a linear multistep method have to satisfy p+1 linear equations. As 2k+1 free parameters are involved, (without loss of generality one can assume αk=1), this suggests that 2k is the highest attainable order. According to Dahlquist (1956), “The order p of a stable linear k –step method satisfies the following conditions:

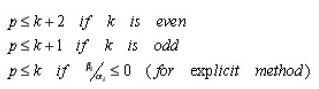
 equation 10

Predictor –Corrector Methods

The idea behind this is that an Adams-Bash forth formulae is used to estimate the value of y(xk+1) and this is then used in place of yk+1 on the right-hand side of an Adams- Moulton formula in order to obtain an improved estimate for yk+1. The Adams Bashforth method is thus used to predict the value yk+1 and the Adams Moulton formula is the corrector which may be applied iteratively until convergence.

Methodology

For the k- step implicit Adams method, we seek 

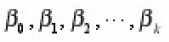
equation 19

that is F(t) = F(xk + ht) = 1,t,t2,t3 ,…tk  

We require 

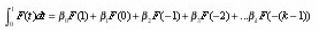
equation 11

 thus we have the following equations to solve:

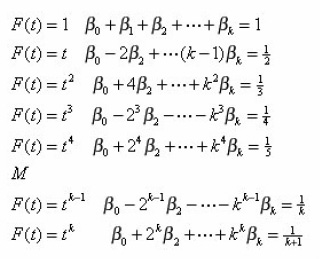
equation 12

We seek the values of the coefficients βj so that the corresponding formula has the maximum possible degree of precision.

To confirm this methodology, we show for step k = 3 for the Adams- Moulton scheme as follows:

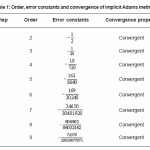
Table 1: Order, error constants and convergence of implicit Adams methods

table 1
Click on image to enlarge

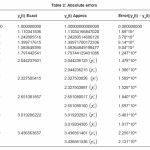
 Table 2: Absolute errors

table 2
Click on image to enlarge

For the three – step Adams Moulton method,

We seek

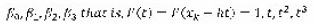
equation 13

we require

we have the following equations

equation 15

Solving the martrix equation for

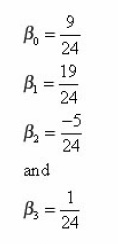
equation 16

and

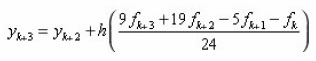
equation 16a

This yields the formula

Following the same procedure we derive the following higher orders:

equation 17

Stability Accuracy and Convergence Analysis of the Methods

Using the definitions in Section 1, above, the computed order of accuracy, and the convergence analysis of the methods are presented in the table 

It is clear that the methods are of orders k+1 whenever k is the step, and all the methods are convergent.

Numerical Experiment and Results

To implement any of the methods, just like any implicit multistep method we need a predictor and in this case we develop explicit methods of the same steps for implementation as in Lambert (1991). In this paper we implement the step six implicit method which is of order seven and we use a step six order six explicit method as the predictor.

Example 1

We consider the ivp.

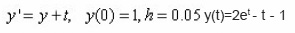
equation 20

Using the step six order five explicit method below

equation 18

as predictor for the step six order seven methods

The table below shows the absolute errors which is of at least order O(h6)

Conclusion

The proposed methods have been shown to be accurate and efficient. They provide option for continuous output. Further improved accuracy can be achieved by block hybrid methods for numerical derivatives combined with self-starting block hybrid methods for the direct integration of.

References

  1.  Butcher, John C, Numerical Methods for Ordinary Differential Equations, John Wiley, ISBN 978-0-387-90277-7 (2003).
    CrossRef
  2.  Butcher, John C, Numerical Methods for Ordinary Differential Equations, John Wiley & Sons Ltd, Chichester, England (2008).
    CrossRef
  3. J.Fatokun, P.Onumanyi and U.W. Sirisena., A Multistep Collocation based on Exponential Basis for Stiff Initial Value Problems. Nigerian Journal of Mathematics and Applications 12: 207-223 (1999).
  4. Fatokun, P. Onumanyi and U.W. Sirisena,Solution of First Order Finite Difference Method with Arbitrary Basis, Journal of Mathematical Society of Nigeria, 24: 30-40 (2005).
  5.  J.O.Fatokun., A Fifth Order Collocation Method for Solving First Order Initial Value Problems. Jour. Inst. Maths. & Computer Sciences (Comp. Sc. Ser.) 17(1): 73-79 (2006).
  6.  Fox, L. in Gladwell, I. and Sayers, D.K. (eds.),Computational Techniques for Ordinary Differential Equations. Academic Press (1980).
  7.  Gear C.W., Numerical initial value problems in Ordinary Differential Equations, Prentice Hall (1971).
  8.  Goldstine, Herman H., A History of Numerical Analysis from the 16th through the19th century, New York: Springer-Verlag, ISBN 978-0-471-96758-3 (1977).
  9. Iserles, Arieh, A first course in the Numerical Analysis of Differntial Equations, Cambridge University Press, ISBN 978-0-521-55655-2 (1996).
  10.  Lambert J.D. Computational methods in Ordinary Differntial Equations, John Wiley.
  11.  P. Onumanyi, Progress in the Numerical Treatment of Stiffness at the 15th Inaugural Lecture Series, held on 30th September, 2004. University of Jos, Jos, Nigeria (2004).
  12.  P. Onumanyi, D.O. Awoyemi, Jator, S.N. and U.W. Sirisena, New Linear Multistep Methods with Continuous Coefficients for First Order IVPs. Journal of Mathematical Society of Nigeria, 13: 37-51 (1994).
  13.  P. Onumanyi, U.W. Sirisena, J.P. Chollom, Y.A.Yahaya and Yusuph Skwame, New Multivalue Multistep Implicit RKMs based on AML Collocation Points for Stiff Ordinary Differential Equations, A paper delivered at the One-day Seminar on Recent Numerical Methods for Solving Differential equations, organised and Proceedings printed at the National Mathematical Centre, Kwali – Abuja, Nigeria, pp 25–58 (2005).
  14.  Turner, Peter, Guide to Numerical Analysis, Macmillian Education LTD, ISBN 0-333-44947-9 (1989).
    CrossRef
Share Button

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

Designed by: Designtohost
Copyright © 2024 MSRI