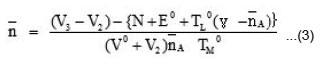Views 
   PDF Download PDF Downloads: 828

 Open Access -   Download full article: 

Stability Constants of Lanthanide Metal Ions Chelates with Substituted Pyrazoles in Different Solvents

G. H. Murhekar*, A. R. Raut and R. S. Sonone

Department of Chemistry, Arts and Science College, Murtizapur, Dist. - Akola - 444 107, India.

DOI : http://dx.doi.org/10.13005/msri/080119

Article Publishing History
Article Received on : 03 May 2011
Article Accepted on : 17 June 2011
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:

The reaction of Pr (III) and Nd (III) metal ions with some substituted pyrazoles, at 0.1M ionic strength and at 30 ± 0.10C in 70% acetone-water mixture and 70% propanol-water mixture have been studied pH-metrically. The data obtained were used to estimate the values of proton-ligand (pK) and metal-ligand (logK) stability constants in different solvents. It is observed that the pK and logK values in 70% propanol-water mixture are grater than in 70% acetone -water mixture. Pr (III) and Nd (III) metal ions formed 1:1 and 1:2 complexes with all the ligands in both solvent medium.

KEYWORDS: Solvent effect; Stability constants; Chelates; Substituted pyrazoles

Copy the following to cite this article:

Murhekar G. H, Raut A. R, Sonone R. S. Stability Constants of Lanthanide Metal Ions Chelates with Substituted Pyrazoles in Different Solvents. Mat.Sci.Res.India;8(1)

Copy the following to cite this URL:

Murhekar G. H, Raut A. R, Sonone R. S. Stability Constants of Lanthanide Metal Ions Chelates with Substituted Pyrazoles in Different Solvents. Mat.Sci.Res.India;8(1). Available from: http://www.materialsciencejournal.org/?p=2520

Introduction

Pyrazoles falls in the class of aromatic heterocyclic compounds, and unique structural feature involving pyrazolic nitrogen and make them interesting ligands. Pyrazoles are the good complexing agent.1-3 The metal ligand stability constants of transition metal ions complexes with some substituted pyrazoles and pyrazolines have been reported.4-5 The influence of ionic strength on the stability constants of transition and lanthanide metal ions complexes with substituted pyrazoles has also reported 6. Ultrasonic properties of some substituted pyrazoles have studied recently.7 Stability constants of transition metal ion complexes with substituted pyrazoles was studied and observed that, ligand L1 is better chelating agent than the ligand L2.8 The interactions of some lanthanide metal ions with substituted isoxazolines at 0.1M ionic strength have been reported pH metrically.9-12 There is wide interest in studying the lanthanide ions in view of expansion of coordination sphere.13-15 Recently ultrasound promoted synthesis of substituted pyrazoles and isoxazoles have reported.16 The effect of various mixed aqueous solvents on the stability constants of Cu (II) chelates with pperidine-2- carboxylic acid have been reported.17 Influence of ionic strength and stability constants of substituted pyrazoles with lanthanides metals ions and effect of composition of solvent have recently studies in our laboratory.18-20 

The study of proton-ligand stability constants and metal-ligand stability constants of Pr (III) and Nd (III) metal ions with some substituted pyrazoles in different solvent mixture have been focus due to their wide range application in various field of human interest. In present research work we have undertaken the chelating properties of, 

L : 3 (2’- chlorophenyl) – 4- benzoyl – 5 (2-hydroxy phenyl) pyrazole,

L : 3 (2’-chlorophenyl) – 4- pyridoyl -5 (2-hydroxy phenyl) pyrazole, 

L : 3 (2’-aminophenyl) – 4-pyridoyl – 5 (2- hydroxyl phenyl) pyrazole and 

L : 3 (4’-chlorophenyl) – 4-Benzoyl -5(2-hydroxy-phyenyl) pyrazole in 70% acetone-water mixture and 70% propanol-water mixture at 0.1 M ionic strength pH metrically.

Experimental

Substituted pyrazoles mention above was synthesized in our laboratory by standard method.21 The substituted pyrazoles are insoluble in water; hence 70% acetone-water (v/v) and 70% propanol-water (v/v) was used as solvent. Lanthanide metal nitrates (Merck, 99.95%) were dissolved in triple distilled water and their concentration estimated by standard method.22 Sodium hydroxide (Merck, 99.99%), potassium nitrate (Merck, 99.99%) and nitric acid (Merck, 99.98%), were used. Propanol and acetone was purified by standard method.23 pH measurement were carried out with ELICO pH meter (accuracy ± 0.05 units) using combined electrode at 30 ± 0.10C.

Calvin-Bjerrum Titration Technique

The titrations were carried out in an inert atmosphere of nitrogen. The ionic strength of solution was maintained constant by adding an appropriate amount of 1M KNO3 solution. The values were recorded by pH meter. These values converted to [H+] values by applying the correction proposed by Van Uitert & Hass.24 The contribution of the other ions in addition to K+ and NO–3 also taken into consideration. The overall 0.1 ionic strength of solution was calculated by expression

equation 1

Results and Discussion

The titration data were used to construct the curve between volumes of NaOH Vs pH. They are called as acid titration curve, ligand titration curve and metal titration curve. The pK values of ligand and logK values of Pr (III) and Nd (III) complexes at 0.1 M ionic strength were calculated by Irving and Rossotti’s method.25

Proton – Ligand Stability Constants (Pk)

Substituted pyrazoles may be considered as monobasic acids having one replaceable H+ ion from phenolic – OH– group and can therefore be represented as HL

equation a

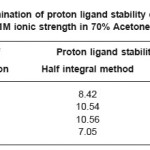
The titrations data in 70% acetone-water mixture were used to construct the curve between volumes of NaOH Vs pH. It is observed from the titration curve that the ligand curves start deviating from free acids curve at about pH 3.51 for L1, at about pH 2.82 for L2 , at about pH 3.46 for L3 and at about pH 2.89 for L4. The deviation increased continuously up to pH 12.50. It indicated that OH–group starts to dissociate at about 2.82 and complete its dissociation at about pH 12.50. (Table 1)

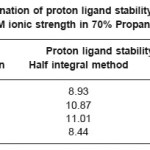
The titrations data in 70% propanol-water mixture were used to construct the curve between volumes of NaOH Vs pH (Fig- I & II). It is observed from the titration curve that the ligand curves start deviating from free acids curve at about pH 3.55 for L1, at about pH 2.90 for L2, at about pH 3.40 for L3 and at about pH 2.96 for L4. The deviation increased continuously up to pH 12.56. It indicated that OH– group start to dissociated at about 2.90 and complete its dissociation at about pH 12.57. (Table 2).

The average number of proton associated with the ligand (A) was determined from ligand titration curves employing the equation of Irving and Rossotti.25

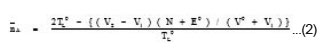
 equation 2

Where, V0 is the initial volume of the solution, E0 and TL0 are the initial concentration of free acid and ligand respectively. V1 and V2 are the volumes of the alkali of a given normality N required. The pK values were estimated from formation curves (A Vs pH) by noting the pH, at which A = 0.5. 

The accurate values of pK were estimated by pointwise calculations. The pK values of ligands increases in the following order in both the solvents. (Table 1 and 2).

Ligand- 03 > Ligand-02 > Ligand-01 > Ligand- 04

The more reduction in pK values of ligand L4 may be due to presence of chlorophenyl and benzoyl groups which act as stronger electron withdrawing groups. Change in pK values in different solvent mixture is due to the polarity of solvents.

Table 1: Determination of proton ligand stability constants (pK) of ligands at 0.1M ionic strength in 70% Acetone-water mixture

Table 1
Click on image to enlarge

Table 2: Determination of proton ligand stability constants (pK) of ligands at 0.1M ionic strength in 70% Propanol-water mixture

Table 2
Click on image to enlarge

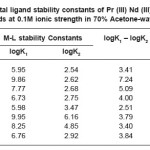
Table 3: Metal ligand stability constants of Pr (III) Nd (III) complexes with ligands at 0.1M ionic strength in 70% Acetone-water mixture

Table 3
Click on image to enlarge

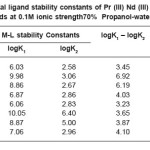
Table 4: Metal ligand stability constants of Pr (III) Nd (III) complexes with ligands at 0.1M ionic strength70% Propanol-water mixture

table 4
Click on image to enlarge

Metal – Ligand Stability Constants ( Logk )

Metal ligand stability constants of Pr (III) and Nd (III) complexes with some substituted pyrazoles were determined by employing Calvin-Bjerrum pH-metric titration technique as adopted by Irving and Rossotti.

The formation of chelates between Pr(III) and Nd(III) with substituted pyrazoles in 70% acetone-water mixture was indicated by,

The significant departure starting from pH 2.94 for Pr (III) and pH 2.91 for Nd (III) complex systems.

The change in colour from, colourless to yellow and then dark yellow as pH increased from 2.98 to 12.50.

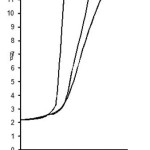
The formation of chelates between Pr(III) and Nd (III) with substituted pyrazoles in 70% propanol-water mixture was indicated by,

The significant departure starting from pH 3.00 for Pr (III) and pH 2.94 for Nd (III) complex system.

The change in colour from, colorless to yellow and then dark yellow as pH increased from 2.97 to 12.55.

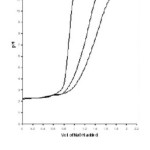
The logK values were directly read from the formation curves ( Vs PL) using half integral method. can be calculated by using following expression

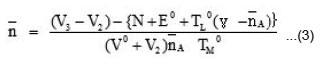
equation 3

Where, N, E0 and TL0 have same significance as per the ligand titrations and V3 represents the volume of alkali required to obtain the same pH as the ligand and acid titration.

Figure 1: Formation of chelates between Pr (III) and Nd(III) with substituted pyrazole 0.1M ionic strength in 70% Acetone-water mixture

figure 1
Click on image to enlarge

Figure 2: Formation of chelates between Pr (III) and Nd(III) with substituted pyrazole 0.1M ionic strength in 70% Propanol-water mixture

figure 2
Click on image to enlarge

Conclusion

The most accurate logK values were calculated by pointwise calculation method. For all the systems and for both solvents (Table 3 and 4). The logK1 and logK2 values follow the order as Pr (III) < Nd (III).

It could be seen that logK values follow increasing trend. This is due to the electron withdrawing group (Cl–, Br– and I–). The values of logK, (logK1 – logK2), and (logK1 / logK2) are in good agreement with excepted values. It is observed that the similar difference may be due to ‘ ‘trans structure’’.

The results show that, the ratio logK1 / logK2 is positive in all cases. This implies that there is little or no steric hindrance to the additions of secondary ligand molecule. The values of pK and logK in various solvents are changed; it is mainly due to polarity of solvents and solubility of restrictions.

The pK values of all the ligands and logK for all system at 0.1M ionic strength at 30 ± 0.10C is grater in 70% propanol-water mixture than 70% acetone-water mixture due to change in dielectric constants of water in the presence of organic solvent, change in structure, hydrogen bonding in water, relative solvent basicity and proton solvation of organic solvent.

The linear relationship logK = a pK + b has been found,26 to hold good for transition metal complex of series of closely related ligands. The stability of the metal complexes of substituted pyrazoles follows the order Pr (III) < Nd (III).

The plot of logK1 Vs pK and logK2 Vs pK show satisfactory linear relationship giving slope values of 1.00 and 1.05 respectively. The partial molar free energies of metal ligand and proton ligand complexes exactly compensate with each other. When logK Vs pK plot is linear with a slope of unity.

Acknowledgements

The authors are very thankful to the UGC, New Delhi, for financial support.

References

  1.  S. C. Jain, M. S. Gill and G. S. Roo, Ind. J. Chem. Lx III: 195 (1986).
  2. R. Rossi and E. Ruvedda , ARKIVOC, 10: 209 (2003).
  3. S.R. Lukic, V. M. Leovac, Mano metal org. Chem.; 31(05): 873 (2002).
  4. P.D. Sawalakhe and M.L. Narwade, J. Ind. Chem. Soc.; 71: 49 (1994).
  5. A.R. Raut and T.H. Mhaske, Acta Ciencia Indica, XVC, 3: 243 (1989).
  6. P.B. Agrawal, A.S. Burghate and M.L. Narwade, Orient J. Chem., 17(1) (2001).
  7.  G.H. Murhekar, A.R. Raut and V.W. banewar, J. Ultra Chem.; 5(3): 337 (2009).
  8.  V.S. Jamode and A.S. Kale, Asian J. Chem.,12 (1): 787 (2007).
  9.  Y.K Mashram, M.L. Narwade, ,Asian J. Chem., 19(1): 493 (2000).
  10.  R. Singhal, V. Tiwari and S. Limaye, J. Ind Chem. Soc; 81 (2004), 207.
  11. M.D. Graham, A. Harry and D.W. Michael,Acta cryst, C-61: 221 (2005).
  12.  Kishor Arora and Kiran Burman, Orient J. Chem. 22(2): (2006).
  13.  A.R. Raut and T.H. Mhaske, J. Ind. chem. Soc., 82: 782 (1985).
  14.  A.R. Raut ; Ph.D. Thesis, Amravati University, Amravati, (1988).
  15.  A.R. Raut and S.T. Mhaske, Orient. J. Chem. 24(1): 223 (2008).
  16.  TS Salah , ET- Rahaman NMA, Ultrasonic Sonachem, 16(2): (2009).
  17.  C. Rebello, G. Shashikala and M. Reddy, Ind. Acad. Sci., 95: 541 (1985).
  18.  G.H. Murhekar, A.R. Raut and V.W. banewar, Orient. J. Chem., 25(4): 1093 (2009).
  19.  G.H. Murhekar, A.R. Raut, and M.L. Narwade, Material Sci. Res, 6(2): 559 (2009).
  20.  G.H. Murhekar , A.R. Raut, Archives of Applied Sci. Research, 2(1): 8 (2010).
  21.  G.H. Murhekar, M. Phil. Dissertation, SGB Amravati University Amravati, (2008).
  22.  A. I.Vogel, A text book of quantitative inorganic analysis, P – 589 (1975). 
  23. A.I. Vogel, Text book of practical organic chemistry; , P-177 (1956).
  24. L.G. Van, Vitert and C. Hass C., J Am Chem. Soc; 75: 451 (1953).
  25. H.M. Irving and H.S. Rossotti , J Chem. Soc.; 3397 (1953).
    CrossRef
  26. J. G. Hones, J. B. Tomkinson and J. P. Williams, J. Chem. Soc.; 3125 (1958).
Share Button

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

Designed by: Designtohost
Copyright © 2024 MSRI