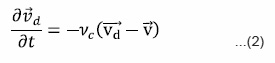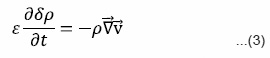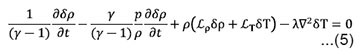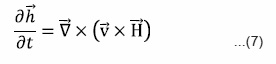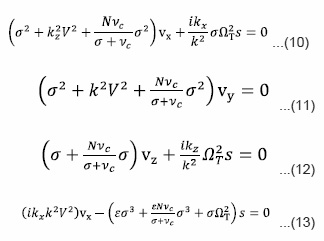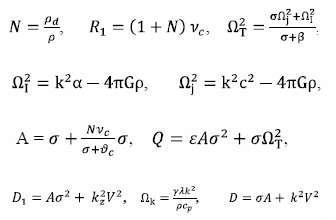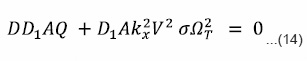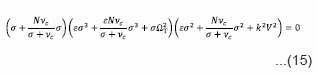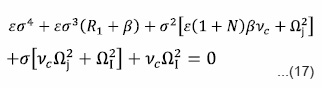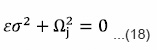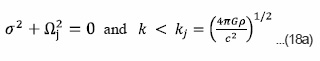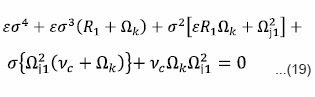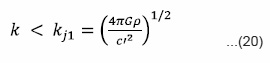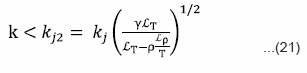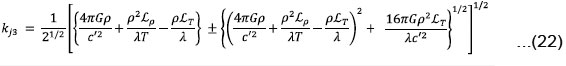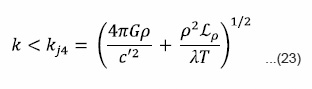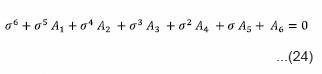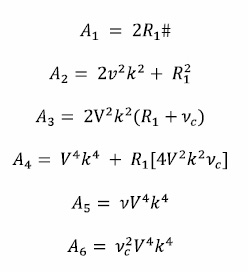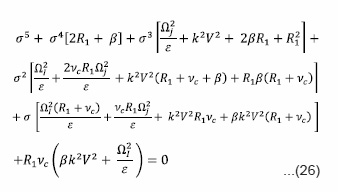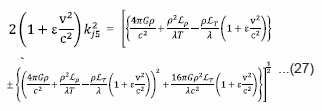Ram K. Pensia, V. Shrivastava, Vishal Kumar, Ashok K. Patidar and Vikas Prajapat
Government P.G. College Neemuch, India.
DOI : http://dx.doi.org/10.13005/msri/080126
Article Publishing History
Article Received on : 07 Jan 2011
Article Accepted on : 13 Feb 2011
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:
The effect of radiative heat-loss function on the Jeans instability of an infinitely conducting, homogeneous partially ionized gaseous plasma is investigated. It is assumed that the medium is carrying a uniform magnetic field in the presence of porosity and thermal conductivity. With the help of relevant linearized perturbation equations of the problem, a general dispersion relation is obtained for a such medium using the normal analysis technique, which is reduced for both the transverse and the longitudinal mode of propagation. The longitudinal mode is found to be modified by Alfven speed and parameter of porosity. The thermal mode is obtained separately having the effects of thermal conductivity and arbitrary radiative heat-loss functions. The effect of collision with neutrals and magnetic field have a stabilizing effect, while thermal conductivity has destabilizing influence on the Jeans instability of gaseous plasma. In the transverse mode of propagation, we find the condition of radioactive instability depends on thermal conductivity, magnetic field and the porosity of the medium.
KEYWORDS:
Porosity; Arbitrary radiative heat-loss function; Partially-ionized plasma; Thermal conductivity and collision-frequency.
Copy the following to cite this article:
Pensia R. K, Shrivastava V, Kumar V, Patidar A. K, Prajapat V. Thermal Instability of Self-Gravitating Partially-Ionized Gaseous Plasma. Mat.Sci.Res.India;8(1)
|
Copy the following to cite this URL:
Pensia R. K, Shrivastava V, Kumar V, Patidar A. K, Prajapat V. Thermal Instability of Self-Gravitating Partially-Ionized Gaseous Plasma. Mat.Sci.Res.India;8(1). Available from: http://www.materialsciencejournal.org/?p=2575
|
Introduction
Much theoretical effect has gone into understanding the gravitational collapse of a protostar but the question of gravitational instability in the presence of radiative heat-loss functions in the infinite homogeneous particular interest in cosmogony. By considering plane wave perturbations to an infinite uniform medium, Jeans¹ has obtained that the disturbances would grow if their wave length exceeded a certain minimum λj is given by λ2 j = π c ² / Gρ Where ρ and c denote the density and sound velocity respectively and G is the gravitational constant. A detailed account of the gravitational instability, under varying assumption of hydrodynamics and hydromagnetic has been discussed by Chandrashekar.2 The Jeans instability has been extensively studied under varying assumption. In this connection, many investigators have discussed the Jeans instability of homogeneous plasma considering the effects of various parameters [Herrenegger,3 Langer,4 Chhonkar and Bhatia,5 Strittmatter,6 Sharma and Thakur,7 Chhajlani and Vaghela,8 Lehnert.9 Recently Pensia et al.10 have discussed the problem of thermal instability of self gravitating, rotating gaseous plasma with generalized ohm’s law. Prajapati et al.,11 have studied the problem of self-gravitational instability of rotating viscous Hall plasma with arbitrary radiative heat-loss functions and electron inertia. The role of magnetic field in contraction and fragmentation of interstellar clouds has been investigated by Pensia et al.,.12 The effect of suspended particles on the gravitational instability of magnetized, viscous gaseous plasma incorporating electric conductivity and Hall plasma has been discussed by Pensia et al.,.13
In interstellar medium there are several situations such as chromospheres, solar photosphere and in cool interstellar cloud where the plasma are frequently not fully-ionized but many instead be partially-ionized so that the interaction between the ionized fluid and the neutral gas becomes important. Alfven14 have discussed the importance of collisions of neutral gas with ionized gas on the ionization rate in these interstellar medium. Kumar and Srivastava15 have studied the gravitational instability of partially-ionized plasma carrying a uniform magnetic field with Hall Effects. The problem of Jeans instability to a stationary self-gravitating cloud has been discussed by Codez.16 Ali and Bhatia17 have investigated the effect of Hall current and finite electrical conductivity in a partially-ionized plasma with oblique magnetic field. Bhatia and Hazarika18 have studied the problem of gravitational instability of partially-ionized plasma in an oblique magnetic field.
In addition to this, the problem of thermal instability arising owing to various heat mechanism of interstellar matter is of considerable importance in connection with astrophysical condensation and the formation of prominences through condensation of coronal material. Field19 have studied the phenomenon of thermal instability arising due to heat-loss mechanism in dilute plasma. In the recent ISM observations, it has been found that the radiative heat-loss mechanism plays an important role in the star formation in molecular cloud condensations process in connection with thermal instability. ISM structure indicates that the heat-loss process is major cause for the condensation of large astrophysical compact objects. Basically these radiative heat-loss functions shows the decay of heat in embedded system with respect to local temperature and density.
Therefore, it would be of importance to examine the effect of arbitrary radiative heat-loss function and collision frequency for two-component gaseous plasma in uniform magnetic field.
Linearized Perturbation Equations
We assume that the two components of the partially ionized plasma (the ionized fluid and the neutral gas) behave like a continuum fluid and their state velocities are equal. The effects of the magnetic field, field of gravity and the pressure on the neutral component are neglected. The fluid is allowed the flow through porous medium. Also it is assumed that the frictional force of the neutral gas
on the ionized fluid is of the same order as the pressure gradient of the ionized fluid. Thus, we are considering only the mutual frictional effects between the neutral gas and the ionized fluid. It is assumed that the above medium is permeated with a uniform magnetic field H (0, 0, H).
Thus the linearized perturbation equations governing the motion of hydromagnetic thermally conducting two components of the partially ionized plasmas are given by
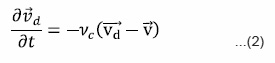
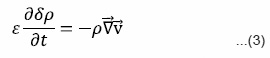
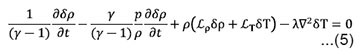

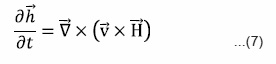

The parameters ϕ, G, λ, R, c, ρ, ρd, υc, γ, t, T, ε and p denote the gravitational potential, gravitational constant, thermal conductivity, gas constant, velocity of light, density of ionized component, density of neutral component (ρ>>ρd), collision frequency between two components, ratio of two specific heats, temperature, porosity and pressure, respectively.
Dispersion Relation
We assume that all the perturbed quantity vary as exp. {i(kxx+kzz+ωt)}. Where ω is the frequency of harmonic disturbances, kx,z are wave numbers in x and z direction, respectively, such that K2x+K2z=k2 combining equation (5) and (6), we obtain the expression for δp as

where, σ=iω, c=(γp/ρ)½ is the adiabatic velocity of sound in the medium
Using equation (2) – (9) in equation (1), we obtain the following algebraic equations for the amplitude components
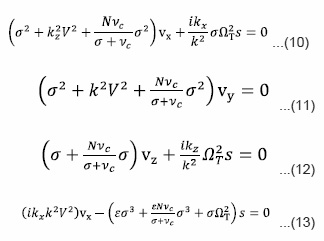
Where S=dρ/ρ is the condensation of the medium, V=H/(4πρ)½ is the Alfven velocity, c2 = γc’2 where c and c’ are the adiabatic and isothermal velocities of sound. Also wee have assumed the following substitutions
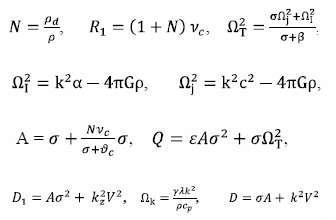
The non trial solution of the determinant of the matrix obtained from equation (10) to (13) with vx, vy, vz, s having various coefficients that should vanish is to give the following dispersion relation
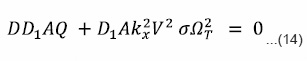
The dispersion relation (16) shows the combined influence of thermal conductivity and arbitrary radiative heat-loss functions on the self gravitational instability of a two components of the partially-ionized plasmas we find that in this dispersion relation the terms due to the arbitrary radiative heat-loss function with thermal conductivity have entered through the factor Ω2T.
Analysis of the Dispersion Relation
Longitudinal Mode of Propagation
For this case we assume all the perturbations longitudinal to the direction of the magnetic field i.e. (kz=k, kx = 0). This is the dispersion relation reduces in the simple form to give
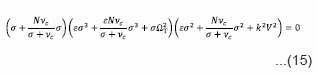
We find that in the longitudinal mode of propagation the dispersion relation is modified due to the pressure of neutral particles, thermal conductivity and arbitrary radiative heat-loss functions. This dispersion relation has three independent factors, each represents the mode of propagation incorporating different parameters. The first factor of this dispersion relation equating to zero
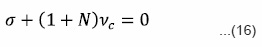
This represents stable mode due to collision frequency. The second factor of equation (15) equating to zero, we obtain following dispersion relation
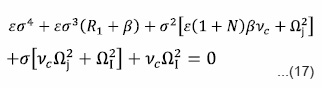
This dispersion relation for self gravitating fluid incorporated effect of neutral particles, porosity, thermal conductivity and arbitrary radiative heatloss function. It is evident from equation (17) that the condition of instability is independent of magnetic field. The dispersion relation (17) is a fourth degree equation which may be reduced to particular cases so that the effect of each parameter is analyzed separately. For thermally nonconducting, non-radiating, fully ionized fluid we have α = β = νc= 0 the dispersion relation (17) reduces
to
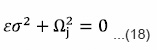
Further more if ignored the porosity i.e. ε= 1, then the dispersion relation (18) reduces to
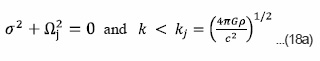
The fluid is unstable for all Jeans wave number k < kj. It is evident from equation (18a) that Jeans criterion of instability remains unchanged in the presence of neutral particles.
For non-arbitrary radiative heat-loss function but thermally conducting and self-gravitating fluid having neutral particles, the dispersion relation (19) reduces to
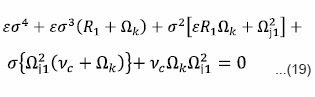
From equation (19) we gat
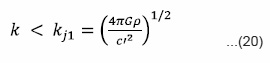
It is clear from equation (20) that the Jeans length is reduced due to thermal conduction [as γ >1], thus the system is destabilized. If we consider self-gravitating and thermally non-conducting plasma incorporated with neutral particles, arbitrary radiative heat-loss function then the condition of instability is given as
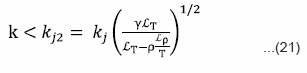
where kj2 is the modified critical wave number due to inclusion of arbitrary radiative heatloss function. Comparing equation (18a) and (21) we find that the critical wave number kj2 is very much different from the original jeans wave number kj and depends on derivatives of the arbitrary radiative heat-loss function with respect to local temperature LΤ and local density Lρ in the configuration. It is clear from equation (16) that when the arbitrary radiative heat-loss function is independent of density of the configuration (i.e. Lρ = 0). Then i.e. critical wave number remains unaffected and if the arbitrary radiative heat-loss function is independent of temperature (LT = 0) then vanishes.
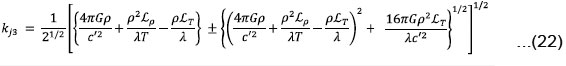
Furthermore, if it is considered that the arbitrary radiative heat-loss function is purely density dependent (LT=0) then the condition of instability is given as
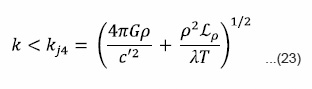
It is evident from inequality (22) that the critical wave number is increased or decreased, depending on whether the arbitrary radiative heatloss function is an increasing or decreasing function of the density.
Now equating zero the third factor of equation (15) and after solving we obtain dispersion relation as
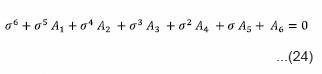
where
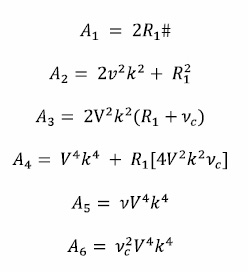
This dispersion relation shows the combined influence of magnetic field and the effect of the neutral particles, but this mode is independent of thermal conductivity, arbitrary radiative heat-loss function and self gravitation. This equation gives Alfven mode modified by the dissipative effect of the neutral particles.
Transverse Propagation
For this case we assume all the perturbations are propagating perpendicular to the direction of the magnetic field, for, our convenience, we take kx=k and kz=0 the general dispersion relation (16) reduces to
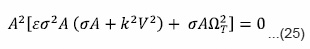
This is the general dispersion relation for transverse propagation shows the combined influence of magnetic field, self-gravitation, porosity,thermal conductivity presence of neutral particles and arbitrary radiative heat-loss function on the selfgravitational instability of a two components of the partially-ionized plasmas. Dispersion relation (25) has two distinct factors, each represents different mode of propagation when equated to zero, separately. Thus the first mode is same as discussed in the dispersion relation (16). The second factor of equation (25) equating zero and substituting the values of a and Ω2T we get
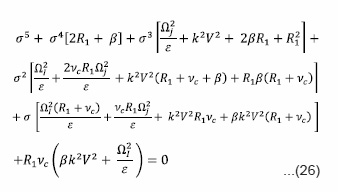
This dispersion relation for transverse propagation shows the combined influence of thermal conductivity, arbitrary radiative heat-loss function on the self-gravitation instability of two components partially-ionized plasmas with the effect of neutral particles and porosity. The condition of instability is obtained from dispersion relation (26) as
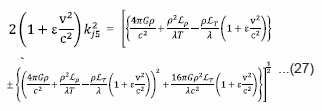
Conclusion
In the present paper, we have investigated the problem of a self gravitational instability of partially-ionized plasma considering the effects of porosity, thermal conductivity and arbitrary radiative heat-loss functions. The general dispersion relation is obtained, which is modified due to the presence of these parameters. This dispersion relation is reduced for longitudinal and transverse modes of propagation. We find that two Jeans criterion for instability remains valid but the expression of the critical Jeans wave number is modified. Owing to the inclusion of the thermal conductivity and isothermal sound velocity is replaced by the adiabatic velocity of sound.
In the case of longitudinal propagation we find a non gravitating Alfven mode modified by the presence of porosity. The thermal mode is obtained separately having the effects of thermal conductivity and arbitrary radiative heat-loss functions. We also found that porosity reduces the effect of the magnetic field.
In the transverse mode of propagation we find a gravitating thermal mode influenced by thermal conductivity and porosity of the medium. We also find that the condition of radiative instability depends on thermal conductivity, magnetic field and porosity of the medium. It is found that the condition of instability and the expression of critical Jeans wave number both are modified due to the presence of magnetic field, thermal conductivity, arbitrary radiative heat-loss function and porosity of the medium. In the case of system, when the arbitrary radiative heat-loss functions are independent of the density of the medium, we find that radiative critical wave number is same as original Alfven critical wave number.
References
- Jeans J.H., “The Stability of Spherical Nebula”, Phil Trans. Ray. Soc. London A199:1-53 (1902).
- Chandrashekhar, S., “Hydrodynamics and Hydromagnetic Stability” Clarendon PressOxford (1961).
- Herrengger F. J., “Effects Of Collisions And Gyroviscosity On Gravitational Instability In A Two-Component Plasma” J. Plasma Physics 8: 393-400 (1972).
- Langer W. D., “The stability of interstellar clouds containing magnetic fields” Astrophysical Space Journal 225: 95 (1978).
- Chhonkar R.P.S., and Bhatia P.K ., “Larmor radius effects on the gravitational instability of two-component plasma”, J. Plasma Physics 18: 273-286 (1977).
- Strittmatter P.A., “A note on gravitational instability in a magnetic medium”, M.N.R.A.S., 131: 491-498 (1966).
- Sharma, R.C. and Thakur, K.P., “The gravitational instability of flow through porous medium for some systems of astrophysical interest” Astrophys. Space Sci. 81:95-102 (1982).
- Chhajlani, R.K. and Vaghela, D.S.,“Magnetogravitational stability of selfgravitating plasma with thermal conduction and finite Larmor radius through porous medium”, Astrophys. Space Sci. 134: 301-315 (1987).
- Lehnert, B., “Plasma-neutral gas interaction in cosmical physics” Astrophysics and Space Science, 55: 25-37 (1955).
- Pensia, R.K. and Ghorela, V., and Chhajlani, R.K., Thermal Instability of a Self Gravitating,Rotating Gaseous Plasma With Generalized Ohm’s Law , Ultra Scientist 20(3): 541-544(2008).
- Prajapati, R.P., Pensia, R.K., Kaothar, S. and Chhajlani, R.K. “Self-gravitational instability of rotating viscous Hall plasma with arbitrary radiative heat-loss functions and electron inertia” Astrophys. Space Sci. 327: 139-154(2010).
- Pensia, R.K. and Kumar, V., and Prajapt, V., “Role of Magnetic field in contraction and fragmen tation of interstellar clouds” , Ultra Science 22(2): 253 (2010).
- Pensia, R.K. and Ghorela, V., and Chhajlani,R.K., “Magneto thermal instability of Selfgravitational viscous Hall plasma in the presence of suspended particle” Acta Ciencia Indica 25(2): 141-148 (2009).
- Alfven, H., “On the origin of the solar system”, Oxford University Press, Oxford (1954).
- Kumar, N. and Srivastava, “K.M. Gravitational instability of partially-ionized plasma carrying a uniform magnetic field with Hall Effect”,Astrophy. Space Sci. 174: 211-216 (1990)
- Cadez, V. M., “Applicability problem of Jeans criterion to a stationary self-gravitating cloud” Astronomy and Astrophysics, 235: 242-244(1990)
- Ali, A. and Bhatia, P.K. “Instability of a gravitating partially-ionized plasma”,Asrtophys. Space Sci. 191: 89-100 (1992)
- Bhatia, P.K. and Hazarika, A. B. R., “Stability of two viscous rotating superposed gravitating streams in a uniform horizontal magnetic field” Phys. Scr. 53: 57 (1996).
- Field, G.B., “Thermal Instability” Astrophys.J. 142: 531-567 (1965).

This work is licensed under a Creative Commons Attribution 4.0 International License.
 Material Science Research India An International Peer Reviewed Research Journal
Material Science Research India An International Peer Reviewed Research Journal