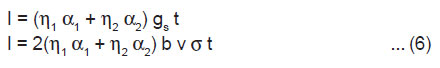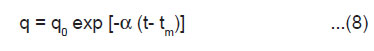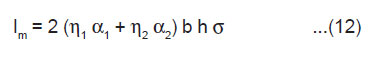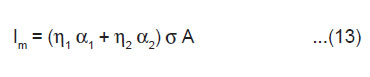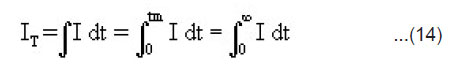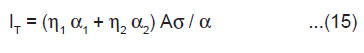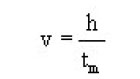Theoretical Approach to Laser Induced Cleavage Mechanoluminescence in Luminophors
M. K. Prajapati1, A. K. Srivastava2 and D. S. Raghuvanshi3
1Dr. C.V. Raman University, Kota, Bilaspur, India.
2Dr. C.V. Raman University, Kota, Bilaspur, India.
3Associate Professor, SSGI, Faculty of Engineering and Technology, Bhilai, India.
DOI : http://dx.doi.org/10.13005/msri/080222
Article Publishing History
Article Received on : 20 Mar 2011
Article Accepted on : 07 May 2011
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:
When a X-ray or g-irradiated alkali halide crystals (AHC) is exposed to 1060 nm infrared pulse of nanosecond duration from CO2 laser, then shock waves produced in the crystals excites visible luminescence due to cleavage of the crystals. This is known as lasser-induced cleavage mechanoluminescence (ML). In the present investigation, NaCl, KCl, NaBr, KBr, and KI crystals are cleaved by laser and ML intensity is recorded. During cleavage, the ML intensity increases and attains a peak value at a particular time and then decays exponentially with time. The total ML intensity increases linearly with the area of the newly created surfaces. A theoretical approach has been proposed to explain the experimental results.
KEYWORDS:
Mechanoluminescence; Cleavage; Alkali halide crystals
Copy the following to cite this article:
Prajapati M. K, Srivastava A. K, Raghuvanshi D. S. Theoretical Approach to Laser Induced Cleavage Mechanoluminescence in Luminophors. Mat.Sci.Res.India;8(2)
|
Copy the following to cite this URL:
Prajapati M. K, Srivastava A. K, Raghuvanshi D. S. Theoretical Approach to Laser Induced Cleavage Mechanoluminescence in Luminophors. Mat.Sci.Res.India;8(2). Available from: http://www.materialsciencejournal.org/?p=2682
|
Introduction
Mechanoluminescence (ML) can be excited by cutting cleaving. grinding rubbing, compressing or by impulsive deformation of solids.1 It is also produced during the deformation caused by drastic cooling or heating of solids5 The ML can be excited by the shock-waves produced during exposure of the materials to laser pulses.6
Fracture of alkali halide crystals along (100) planes is called cleavage. When crystals are cleaved by laser, light emission takes place known as mechanoluminescence (ML).1-4 On cleavage of the crystals, charged surfaces are produced which may cause dielectric breakdown of the solids and the intervening gases. Thus, light emission may take place. The ML excitation produced during cleavage of crystals has not been studied systematically till date. In the present paper, a suitable theoretical approach has been proposed which explains the experimental results on laser-induced cleavage ML of NaCl, KCl, NaBr, KBr and KI crystals. The theoretical approach provides an optical tool do determine crack velocity in crystals.
Theory
When a crystal is cleaved by impact of laser, charged surface are produced due to the processes like charged dislocation movement and baro-diffusion of charged defects near the crack-tip etc.7-8 The surface charge can be neutralized by the charge carriers and ions produced due to the dielectric breakdown of intervening gases and the solids. Thus, depending on the prevailing conditions, the light emission resembling either gas discharge or luminescence of solids or that having these two characters can be obtained.
If a crystal having length l, breadth b and thickness h is cleaved by laser along the plane parallel to its breadth side, rate of creation of new surface is given by 2bv, where v is the average velocity of crack propagation. If σ is the charge density of the newly created surfaces of the crystal, then the rate of generation of surface charge is given by

When the charged surface are created, then the charge density may get relaxed firstly, by the charge carriers produced due to the breakdown of the crystal, and secondly, by the electrons and ions produced due to the breakdown of intervening gases. If α1 and α2 are the rate constants for the relaxation of charges on the newly created surface by the crystal and gaseous breakdown processes, respectively, then we may write the following rate equation

where α = (α1 + α2) and q is the surface charge at any time.
As q = 0 at t = 0, the solution of Eqn. (2) gives
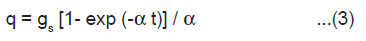
If η1 is the luminescence efficiency related to the movement of carriers produced by the dielectric breakdown of the crystals and η2 is the luminescence efficiency related to the movement of positive electrons and ions produced by the dielectric breakdown of intervening gases, then the ML intensity may be expressed as
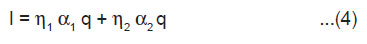
From Eqn.(3) and (4), we get
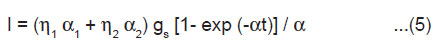
Kinetics of ML
For αt < 1, Eqn.(5) may be written as
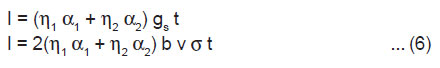
The above equation shows that when a crystal is cleaved, initially the ML intensity should rise linearly with time t.
After the completion of cleavage of the crystal at t = tm, v becomes zero and hence gs=0, at t = tm. Thus, from Eqn.(2), we have

Taking q=q0 at t = tm and integrating Eqn.(7) we get
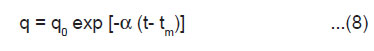
As tm is very short time, negligible discharge occurs within the duration from 0 to tm and, therefore, we may take q0 = 2bhσ, i.e., the total charge on the newly created surfaces. From Eqn.(4) and (8), we get
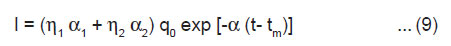
Eqn.(9) shows the exponential decay of the ML intensity after cleavage of the crystals.
Estimation of tm
For the thickness h of the crystal, the time tm taken for cleaving the crystal is given by

The above equation shows that the velocity of crack propagation may be given by

Thus, ML provides a new tool for determining the velocity of crack propagation in crystals. The crack velocity is found to increase with increasing thickness of the crystals.
Estimation of Im
From Eqn.(6) and (10), the value of the peak ML intensity at t = tm is given by
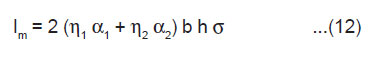
As 2bh is the area A of the newly created surface, we have
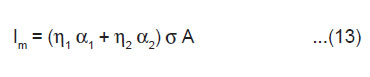
The above equation shows that Im should increase linearly with the area of the newly created surface A and also with the surface charge density σ.
Estimation of IT
The total ML intensity IT i.e. the integrated area below the ML intensity versus time curve may be given by
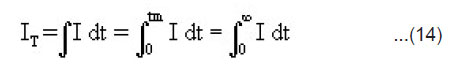
From Eqn.(5),(9) and (14), under the condition 1/α >> h/2v, we may express the total ML intensity as
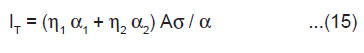
The above equation shows that the total ML intensity should be directly proportional to the area of newly created surfaces A. It is also evident that IT should be higher for the crystals having higher values of the surface charge density σ. In KCl, KBr and KI crystals, surface charge density may be so slow that ML emission is not observed. From the measurements of the ML intensity, the velocity of crack propagation in the material can be determined by using the relation
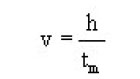
Experimental Support to Theory
Single crystals of NaCl, KCl, NaBr, KBr, and KI of dimensions 1×1×1mm3, 2×2×2mm3 and 3×3×3mm3 were taken. The sample was placed on a transparent lucite plate and was cleaved by 1060 nm infrared pulse of nanosecond duration from CO2 laser. For measuring the ML intensity, a photometer tube whose output was connected to a storage oscilloscope was placed below the transparent lucite plate.
Results
KCl, KBr and KI crystals do not show ML emission during cleavage. In NaCl and NaBr crystals, the ML intensity initially increases with time, attains a peak value Im at a particular time and then decreases exponentially with time. The peak ML intensity Im and total ML intensity IT (=) increases linearly with time the area of newly created surface.
Conclusion
It may be said that the proposed theory explains that when a crystal is cleaved; initially, the ML intensity increases linearly with time, attains a peak value at time tm corresponding to completion of the cleavage of the crystal, and then it decays exponentially with time. The peak intensity of ML increases linearly with the area of the newly created surfaces and also with the surface charge density.
References
- B.P. Chanda, Nuclear Tracks, 10: 825 (1985).
- M.L. Molotskii and S.Z. Shmurak, Phys. Stat.Sol. A166: 286 (1992).
- B.P. Chandra, Lumin. of Solids, Edt. by D.R.Vij, Plenum Press, NewYork, 361 (1998).
CrossRef
- B.P. Chandra, Phys. Stat. Sol., 64: 395 (1981).
CrossRef
- J. Dewar, Nature, 64: 254 (1901).
- G.E. Hardy, B.P. Chandra, J.I. Zink, J.W.Adamson, R.C. Fukuda and R.L. Walters, J.Am., Chem. Soc. 101: 2784 (1979).
CrossRef
- D.V. Alekseev, Sov. Phys.,Solid State, 34:1085 (1992).
- M.I. Molotskii, Sov. Sci. Rev. B, 13: 1 (1989).
- B.P. Chandra, etd Journal of Luminescence,104: 35-45 (2003).
CrossRef
Views: 125
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Material Science Research India An International Peer Reviewed Research Journal
Material Science Research India An International Peer Reviewed Research Journal