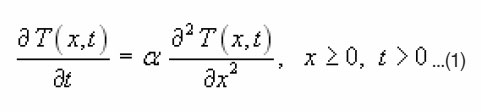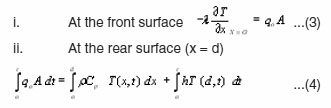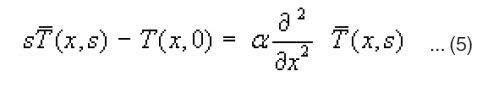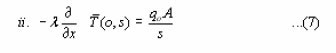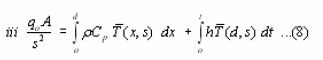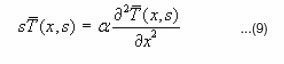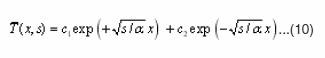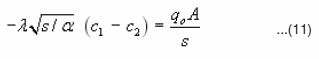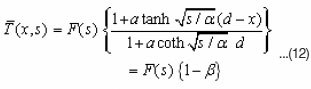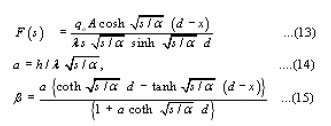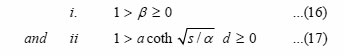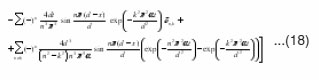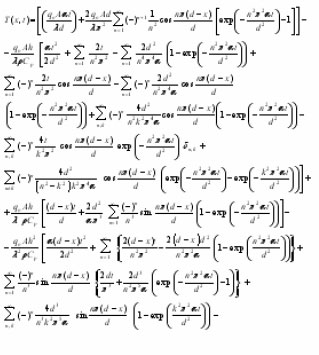Views 
   PDF Download PDF Downloads: 859

 Open Access -   Download full article: 

Heating of a Finite Slab with CW Laser in Relation to Cooling Conditions- at the Rear Surface

M.K. El-Adawi1* and I.A.Al-Nuaim2

1Department of Physics, Faculty of Education, Ain Shams University, Helliopolis, Cairo Egypt

2Physics Department, Faculty of Science for Girls, King Faisal University P.O. Box 838 Dammam 31113 , Saudi Arabia.

Article Publishing History
Article Received on : 25 Apr 2013
Article Accepted on : 26 May 2013
Article Published :
Plagiarism Check: Yes
Article Metrics
ABSTRACT:

Heating a slab induced by laser irradiance is studied. The heat diffusion equation is solved using the Laplace integral transform method. The critical time tm required to initiate melting is obtained for the elements: Aluminum (Al), Gold (Au), Germanium (Ge) and Silicon (Si). Good cooling conditions at the rear surface of the slab are assumed. The obtained results show that for the considered elements and for such sources of high power density, cooling conditions at the rear surface are not of pronouncing effect. The effect of laser power density on the critical time required to initiate melting is predominant.

KEYWORDS: Laser heating; Laser damage; Heat diffusion equation; Laplace transform

Copy the following to cite this article:

El-Adawi M. K, Al-Nuaim I. A. Heating of a Finite Slab with CW Laser in Relation to Cooling Conditions- at the Rear Surface. Mat.Sci.Res.India;10(1)

Copy the following to cite this URL:

El-Adawi M. K, Al-Nuaim I. A. Heating of a Finite Slab with CW Laser in Relation to Cooling Conditions- at the Rear Surface. Mat.Sci.Res.India;10(1). Available from: http://www.materialsciencejournal.org/?p=281

Introduction

Laser heating of materials has aroused  considerable interest1-23 due to its demonstrated importance in many processes for industrial applications such as spot welding, scribing and hole drilling, optical recording, semiconductor materials processing.

Serious trials are made to solve the diffusion equation describing the heating problem subjected to different boundary and initial conditions. The bulk of such trials have been numerically based. Some attempts are treated analytically.12-23

The present treatment represents one of such analytical trials oriented to study the problem of heating a slab considering the cooling conditions at its rear surface using Laplace integral transform technique.

Theory

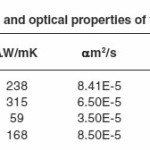
In setting up the problem it is assumed that the slab is subjected to a constant flux of laser irradiance qo (W/m2) incident on the front surface and perpendicular to it. The diameter of the laser beam is assumed to be large compared to the thermal penetration depth within the slab, and thus the problem is solved as a one-dimensional problem.1 The thermal and optical properties are assumed to be temperature independent.

The heat-flow equation for the temperature rise T(x,t) has the form :

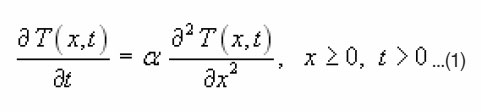
vol_10_No_1_Hea_ADA_equ1

where T(x,t) is the excess temperature with respect to the ambient temperature To, α = λ/ρCp is the thermal diffusion coefficient of the slab in terms of the thermal conductivity λ and the heat capacity per unit volume (ρCp). Eq. (1) is subjected to the initial condition :

vol_10_No_1_Hea_ADA_equ2

And the boundary conditions :

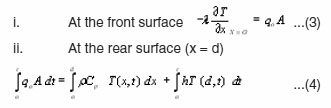
vol_10_No_1_Hea_ADA_equ3&4

 Derivation of the required solution

The Laplace transform of equation (1) with respect to the time variable “t” gives :

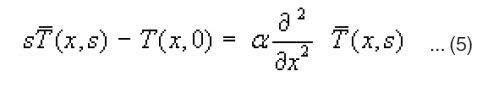
vol_10_No_1_Hea_ADA_equ5

where

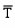
where-T 

(x,s) is the Laplace transform of T(x,t).

One must also write the Laplace transform of the initial and boundary conditions this gives :

vol_10_No_1_Hea_ADA_equ6

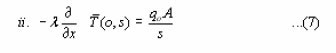
vol_10_No_1_Hea_ADA_equ7

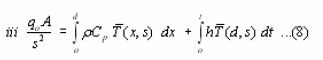
vol_10_No_1_Hea_ADA_equ8

Substituting equation (2) into equation (5) gives :

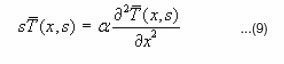
vol_10_No_1_Hea_ADA_equ9

The solution of equation (9) can be written in the form :

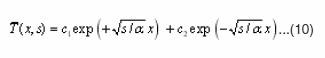
vol_10_No_1_Hea_ADA_equ10

Applying the conditions (6-8) to equation (10) one gets :

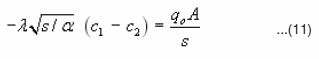
vol_10_No_1_Hea_ADA_equ11

One can determine the values of c1 and c2. The solution can finally be written in the form.

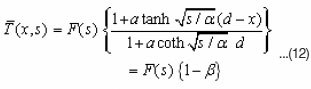
vol_10_No_1_Hea_ADA_equ12

Table 1: The physical and optical properties of the chosen elements

 Click on image to enlarge

 

Table 2
Click on image to enlarge

 

Fig.1
Click on image to enlarge

                                                                             

Fig.2
Click on image to enlarge

 

Fig.3
Click on image to enlarge

                                                                                  

Fig.4
Click on image to enlarge

 

Fig.5

Click on image to enlarge

                                                                               

Fig.6

Click on image to enlarge

 

Where

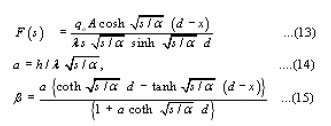
vol_10_No_1_Hea_ADA_equ13,1

It is worth noting that for positive arguments the hyperbolic functions coth(x) and tanh(x) are positive. Moreover, as x increases from zero to + ∞, tanh(x) increases from 0 to +1 while coth(x) decreases from ∞ to 1. This behavior leads to the following conditions :

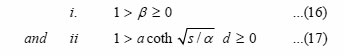
vol_10_No_1_Hea_ADA_equ16,1

The equality represents the case when h = 0, i.e., the case of a thermally insulated rear surface.19

Fig.7
Click on image to enlarge

 

Fig.8
Click on image to enlarge

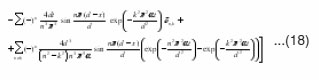
vol_10_No_1_Hea_ADA_equ18

The temperature of the front surface T(0,t) at x = 0 and that of the rear surface at x=d can be easily obtained by substituting x=0 and x=d respectively in equation).18

Using the standard tables of the inverse Laplace transform24 and taking into consideration the convolution property. One can finally get the required solution in the form :

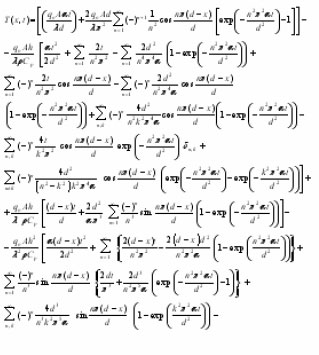
vol_10_No_1_Hea_ADA_equatio

Computations

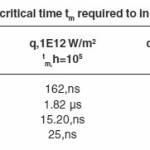
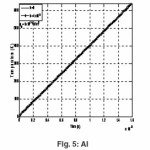
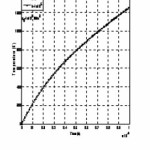
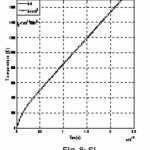
As illustrative examples computations are made to obtain the critical time required to initiate melting tm for the considered elements.

Each target is assumed to be of thickness d = 5 mm and is subjected to constant laser flux of irradiance qo = 1012, W/m2 and q0=1E 14 W/m2. To ensure good cooling conditions high value h = 105

W/m2K of the heat transfer coefficient is also considered at the rear surface.

The physical and optical parameters of the chosen elements are obtained from refs,25, 26 and are given in Table 1

The computed values tm for the considered elements are given in table 2.

Conclusions

The obtained values for tm makes it possible to conclude that: 

1. Cooling conditions at the rear surface of a target exposed to light of high power density are not effective.

2. The difference in the critical time required to initiate damage for h=0 and h=105W/m2K is almost undetectable for such sources of high power densities.

3. The values of the critical time required to initiate melting is strongly dependent on the incident power density and the value of the absorption coefficient of the irradiated surface.

References

  1. Ready, J. F.; Effects Due to Absorption of Laser Radiation. J. Appl, Phys.  (1965); 36(2); pp 462-468.
    CrossRef
  2.  Ready, J.F.; Effects of High Power Laser Radiation. (Academic, New York, Chap. 8). (1971).
  3.  Fairand, B.P., Wilcox, B.A., Gallagher, W.J. and William, D.N.; Laser Shock-induced Microstructure and Mechanical Property Changes in 7075 Aluminium. J. Appl. Phys.  (1972); 43(9); pp.3894.
  4.  E.M. Breinan, B.M. Kear and C.M. Bamas, Processing Materials with Laser’s physics today, pp. 44-50 (1976).
  5.  M. Terao, K. Shigematsu, M. Ojima, Y. Taniguchi, S. Horigoma and S. Yonezawa, Chalcogenide thin Films for Laser-beam Recordings by Creation of holes, J. Appl. Phys. 50(11): PP. 6881-6886 (1979).
  6.  A. Cutolo, P. Gay and S. Solimeno, Mirror Deformations and Wavefront Aberrations Caused by CW High Power Laser Beams, Optica Acta 27(8): PP. 1105-1116 (1980).
  7.  J. Narayan, J. Fletcher, C.W. White and W.H. Christie, Melting Phenomena and Pulsed Laser Annealing in Semiconductors, J. Appl. Phys. 52(12): PP. 7121-7128 (1981).
  8.  D. Kirillov and J.L. Merz, Laser Beam Heating and Transformation of a Ga-As-ALAS, Multiple-quantum-well Structure J. Appl. Phys. 55(4): pp. 1105-1109 (1984).
    CrossRef
  9. S. Kawamura, N. Sasaki, M. Nakano and M. Takagi, Laser Recrystallization of Si over SiO2 with a heat-sink Structure, J. Appl. Phys. 15: pp. 1607-1609 (1984).
    CrossRef
  10.  S.D. Allen, J.A. Goldstone, J.P. Stone and R.Y. Jan, Transient Nonlinear Laser Heating and Deposition : A Comparison of Theory and experiment, J. Appl. Phys. 59(5): 1683-1657 (1986).
    CrossRef
  11.  D. Waechter, P. Schnan, R.E. Thamas and N.G. Tarr, Modeling of Heat Flow in Multilayer CW Laser-annealed Structures, J. Appl. Phys. 59(10): 3371-3374 (1986).
    CrossRef
  12.  J.H. Bechtel, Heating of Solid Targets with Laser Pulses, J. Appl. Phys. 46(4): 1685-1593 (1975).
    CrossRef
  13.  R.E. Warren and M. Sparks, laser Heating of a Slab having Temperature-dependent Surface Absorptance, J. Appl. Phys. 50(12): 7952-7957 .
    CrossRef
  14.  M.M. El-Niclawy, M.K. El-Adawi, A.A. Kutub and G.G. Al-Barakati Analytic Approach for Melting and Evaporation of a Solid by a Pulsed Laser, Acta Physica Hungarica 59(3- 4): 291-296 (1986).
  15.  M.K. El-Adawi and E.F. El-Shehawey, Heating a Slab Induced by a Time-dependent, Laser Irradiance-An Exact Solution, J. Appl. Phys. 60(7): 2250-2255 (1986).
    CrossRef
  16.  M.K. El-Adawi and S.A. Shalaby, Laser Heating and Melting of Thin Films with Timedependent Absorptance. An exact solution for time intervals less than or equal to the transit time. J. Appl. Phys. 63(7): 2212-2216 (1988).
    CrossRef
  17.  B.J. Bartholomeuszm, Thermal Response of a Laser-Irradiated Metal Slab, J. Appl. Phys., 64(8): 3815-3819 (1988).
    CrossRef
  18.  M.K. El-Adawi, S.A. Shalaby and E.F. El- Shehawey and T. El-Dessouki, Laser Heating and Melting of Thin Films with Timedependent Absorptance. An Exact solution for time intervals greater than the transit time, J. Appl. Phys. 65(10): 3781-3785 (1989).
    CrossRef
  19.  M.K. EL-Adawi and S.A. Shalaby, Heating Effects of Laser Irradiance on a Slab with Constant Surface Absorptance. An exact solution, 8th. International Conference on Numerical Methods in Thermal Problems. July 11th – 16th, Swansea, U.K. 1394-1405 (1993).
  20.  M.K. EL-Adawi, M.A. Abdel-Naby, and S.A. Shalaby, Laser Heating of a Slab Having Temperature Dependent Surface Absorptance, 45(1): 65-70 (1994).
  21.  Yilbas B.S. Shuja SZ, Laser Short-pulse heating of Surfaces, J. Phys. D. Appl. Phys. 32: pp.1947-1954 (1999).
    CrossRef
  22.  Al Koc, “3-D Analysis of Temperature Distribution in the Material during Pulse Laser and Material Interaction” Heat Mars Transfer, 10(1): 1007 (2003).
  23.  M.K. El-Adawi, S.A. Shalaby, S.S. Mostofa and M.F. Kotkata, Laser Thermal Response of a Finite slab as a Function of the Laser Pulse Parameters, Optics & Laser Technology 39: 424-429 (2007).
    CrossRef
  24.  M.R. Spiegel, Laplace Transforms (Schaum’s Series), McGraw-Hill, New York 1953,p.45.
  25.  M. Sparks and E. Loh, Jr., Temperature Dependence of Absorptance in Laser Damage of Metallic Mirrors : I. Melting, J. Opt. Soc. Am 69(6): pp 847 (1979).
  26.  E.R.G. Eckert and R.M. Drake, Analysis of Heat and Mass Transfer, Int. Student Edu, McGraw-Hill, Kogakusha, Japan 772 (1972).
  27.  R.C.Weast. Handbook of Chemistry and physics , 59 thed. Florida : CRCPress (1979.
  28.  A.Bhattacharyya and B.G.Streetman, Dynamics of Pulsed CO2 Laser Annealing of Silicon. J. Appl.Phys. 14L: 67-72 (1981).

 

Share Button

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

Designed by: Designtohost
Copyright © 2024 MSRI