Structural, Vibrational, and Electronic Properties of Trigonal Cu₂SrSnS₄ Photovoltaic Absorber from First-Principles Calculations

Sriram Poyyapakkam Ramkumar*

Research Associate, Department of Materials Science and Engineering, University of California, Merced, 95343, USA

Corresponding Author Email: spramkumar@ucmerced.edu

DOI : http://dx.doi.org/10.13005/msri.17.special-issue1.03

ABSTRACT: In the search for sustainable alternate absorber materials for photovoltaic applications, the family of chalcogenides provide a promising solution. While the most commonly studied Cu₂ZnSnS₄ based kesterite solar cells seem to have intrinsic drawbacks such as low-efficiency arising from defects and anti-disorder in the Cu-Zn sites, substituting other elements in the Cu/Zn sites have been considered. In this direction, Cu₂(Ba,Sr)SnS₄ provide an interesting alternative as they possibly help limit the intrinsic anti-site disorder in the system which is of primary concern with regard to efficiency loses. In this study, we report the structural, vibrational, and electronic properties of trigonal structured Cu₂SrSnS₄ quarternary system computed from first-principles density functional theory paving way for further characterization and analysis within this class of materials. KEYWORDS: Chalcogenides; Density Functional Theory (DFT); Density Functional Perturbation Theory (DFPT); Photovoltaics (PV); Vibrational Properties

Copy the following to cite this article: Ramkumar S. P. Structural, Vibrational, and Electronic Properties of Trigonal Cu2SrSnS4 Photovoltaic Absorber from First-Principles Calculations . Mat. Sci. Res. India; Special Issue (2020).

Copy the following to cite this URL: Ramkumar S. P. Structural, Vibrational, and Electronic Properties of Trigonal Cu2SrSnS4 Photovoltaic Absorber from First-Principles Calculations . Mat. Sci. Res. India; Special Issue (2020). Available from: https://bit.ly/3fFIz3j

Short Communication

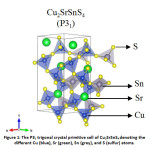
Increasing energy demand moving into the terawatt scale and increasing environmental concerns due to non-renewable sources of energy has caused great concern to humanity. Given the abundance of solar energy available, harnessing it efficiently to mitigate this problem has been propounded for over a decade now. While Si solar cells have reached a commercially viable efficiency, it is still not competent enough to provide a considerable edge over the oil market. Thin film solar cells on the other hand are cost effective, but their efficiencies are not comparable to their Si counterpart. Moreover, the commercial thin-film solar cells contain Cd and Te which are toxic and scarce in nature respectively. In this respect, kesterite solar cells, especially Cu₂ZnSnS₄, has been a sought-after alternative.¹ Despite its numerous advantages including having an ideal bandgap with respect to the Shockley-Queisser limit,² and all the elements being earth-abundant and non-toxic in nature, it falls short in terms of photovoltaic (PV) efficiency. The low open-circuit voltage in kesterites³ leading to low PV efficiency has been attributed to several factors – small phase region of stability,⁴ defects,⁵ and more importantly the cation disorder⁶ in the system. In order to tackle the cation disorder, several substitutions on the Cu/Zn sites (where the disorder primarily occurs) have been considered and their phase stabilities⁷ have been well-established. Among these, Cu₂BaSnS₄, Ag₂BaSnS₄, and Cu₂SrSnS₄ have been synthesized and is found to crystallize in the trigonal structure (as shown in Fig. 1) but not in the kesterite structure unlike the other members.^7,8,9 This is mainly because of the large mismatch of ionic radii: Sr²⁺ > Cu¹⁺/Sn⁴⁺. Further, such an arrangement would benefit in suppressing the intrinsic defect formation (especially deep levels) which is predominant in absorbers such as CZTS due to similar ionic sizes. This could help limit band tailing and electrostatic potential fluctuations in the system which leads to voltage deficit and efficiency loses.^8,10 Furthermore, these materials with bandgaps ranging between 1.5-2.0 eV are likely to be promising candidates for PV absorbers.⁹

Figure 1: The P31 trigonal crystal primitive cell of Cu2SrSnS4 denoting the different Cu (blue), Sr (green), Sn (grey), and S (sulfur) atoms.

Click on image to enlarge

Cu₂SrSnS₄ (CSTS) is considered to be an interesting candidate for both PV and water-splitting applications given its advantages in terms limited disorder between Cu and Sr due to large atomic mismatch and good optical properties.^7,10 While its synthesis has been a challenge similar to Cu₂BaSnS₄, recent experimental works have been able to prepare good quality samples in an efficient way.¹⁰

Though the phase stability and optical properties have been computed and experimentally analyzed in this material, its vibrational properties which are essential for a robust phase analysis as in the case of Cu₂ZnSnS₄¹¹ has not been reported to the best of our knowledge. In order to contextualize them, we use density functional theory (DFT)¹² approach which has been one of the highly sought after computational scheme for the last couple of decades as it is being widely employed for  materials design to analysis to machine learning of properties from first-principles.^13,14,15 We hence perform DFT calculations to obtain the structural properties of CSTS, and further in combination with density functional perturbation theory (DFPT)¹⁶ we obtain the phonon frequencies at Gamma-point of the Brillouin zone. DFT calculations are performed using the Vienna ab initio package (VASP) code¹⁷ using the projected augmented wave (PAW)¹⁸ method treating Cu(3p⁶ 3d¹⁰ 4s¹), Sr(4s² 4p⁶ 5s²), Sn(4d¹⁰ 5s² 5p²), and S(3s² 3p⁴) as the valence electrons. It is to note that the d states are explicitly taken into account for Cu and Sn atoms in order to increase the accuracy of the calculations.  We adopted the PBEsol version of Perdew-Burke-Ernzerhof for the exchange-correlation functional.¹⁹ A k-point mesh corresponding to a density of 1000 k-points per atom centered at Gamma point of the Brillouin Zone and kinetic energy cut-off of 600 eV for the plane wave basis sets were used. The structure was relaxed until forces on the atoms were less than 2 meV/Å while the electronic steps for self-consistency were converged until 10^-8 eV.

The structural parameters for the trigonal CSTS structure are shown in Table 1. Table 2 shows the comparison with lattice parameters and bandgap obtained in this study with those in the literature. The a/b parameters using PBEsol is smaller than those obtained from other exchange-correlation functionals but the c parameter is largely underestimated in comparison to experiment¹⁶ and the HSE hybrid functional parameters in the literature.⁷ It is also important to note that the HSE lattice parameters between Zhu et al.⁷ and Hong et al.⁹ are significantly different from one another (and hence needs further investigation) while our values are closer to that of the latter. The bandgap, on the other hand, shows a value closer to the experiment in comparison to PBE but is much smaller than PBE+U and HSE indicating the importance of onsite Hubbard electron-correlation term in this system similar to CZTS.

Table 1: Theoretical lattice parameters (in Å), atomic positions in reduced coordinates (x,y,z), and Wyckoff sites of Cu, Sr, Sn, and S atoms in the P3₁ trigonal structure of Cu₂SrSnS₄.

Cu2SrSnS4  (P31 space group)
Lattice parameters: a = 6.245 Å, b = 6.245 Å, c = 15.357 Å			Bond angles: = = 90o, = 120o
Atoms/atomic positions	x	y	z	site
Sn(1)	0.33327	0.36920	0.08138	3a
Sr(1)	0.89511	0.66650	0.24806	3a
Cu(1)	0.26345	0.23028	0.33542	3a
Cu(2)	0.69973	0.10272	0.16066	3a
S(1)	0.37746	0.14717	0.20257	3a
S(2)	0.89688	0.18597	0.29351	3a
S(3)	-0.02084	0.43104	0.07719	3a
S(4)	0.68742	0.78509	0.08561	3a

Table 2: Theoretical lattice parameters (in Å) and bandgap (E_g) obtained using PBEsol of P3₁ trigonal structure of Cu₂SrSnS₄ in comparison with experiment²⁰ and theoretical observations^7,9 in the literature.

	a (Å)	b (Å)	c (Å)	Eg (eV)
Experiment16	6.367	6.367	15.833	1.93
HSE7	6.410	6.410	15.862	1.79
HSE9	6.290	6.290	15.578	1.75
PBE+U7	6.393	6.393	15.852	1.62
PBE-GGA7	6.450	6.450	15.867	0.38
PBEsol (this work)	6.245	6.245	15.357	0.46

We further compute the vibrational properties wherein we identify the infrared (IR) and Raman active modes in CSTS. This would help us identify the trigonal CSTS structure in a system of multiple phases as the IR and Raman modes would represent it as a unique fingerprint of the same. Since there are 24 atoms in the primitive cell, we have 3N number of phonon modes (where N is the number of atoms in the primitive unit cell) which is a total of 72 modes out of which 3 are acoustic modes.

Based on group symmetry analysis, the phonon modes for P3₁ (N⁰ 144) can be expressed as:

_a = A ⨁ ¹E ⨁ ²E (acoustic modes)

_o = 23A ⨁ 23¹E ⨁ 23²E (optic modes),

where all of the A, ¹E, and ²E are both IR and Raman active. The ¹E and ²E modes are doubly degenerate and can be represented as E modes. While computing the frequencies using HSE would be ideal, given its computational cost, we restrict with the computation of phonon frequencies with PBEsol. The modes at higher frequencies might change considerably as the sulfur polarizabilities are not well reproduced by non-local exchange-correlation functionals²¹.

Table 3: Transverse optical (TO) phonon frequencies corresponding to A and E modes computed using PBEsol for P3₁ trigonal structure of Cu₂SrSnS₄. The E modes are doubly degenerate comprising of ¹E and ²E modes.

Mode	Frequency (cm-1)		Mode	Frequency (cm-1)
	TO			TO
A	41.7		E	47.4
	53.7			69.3
	58.7			70.6
	71.6			73.5
	77.9			82.9
	83.1			87.5
	90.8			93.2
	93.8			101.0
	111.9			117.0
	121.5			129.8
	142.5			142.8
	156.8			155.3
	164.8			165.9
	171.1			176.5
	186.3			185.6
	274.6			277.6
	280.7			282.4
	287.5			285.6
	318.7			312.0
	318.8			324.9
	342.1			341.8
	354.0			354.2
	357.0			366.5

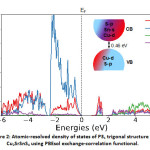
For the electronic properties, while computing the atomic resolved density of states, we note that near the valence band edge, there is a large overlap between Cu and S states, while in the conduction band is occupied by Sn and S states predominantly with significant contribution from Cu as well while there is comparatively negligible contribution from Sr. This is in qualitative agreement with the HSE calculations in the literature,^7,9 hence a significant difference in their band structure.  We also note that despite minor differences, the electronic structure is very similar to the well-known CZTS absorber.^22,23

Figure 2: Atomic-resolved density of states of P31 trigonal structure of Cu2SrSnS4 using PBEsol exchange-correlation functional.

Click on image to enlarge

The density of states is shifted with respect to the Fermi level (E_F) shown as the dashed arrow in the figure. A schematic of the band diagram denoting the valence and conduction bands based on the orbital contribution is provided as an inset. The colour code corresponds to the one represented for the density of states.

In summary, we carry out ab-initio DFT calculations to compute the structural, vibrational, and electronic properties of Cu₂SrSnS₄ in its P3₁ trigonal phase. The structural characteristics are in good agreement with those in the literature given the approximations considered while it is also important to note the discrepancy between the HSE computations in the literature. The PBEsol bandgap shows a smaller error than standard PBE-GGA but is significantly underestimated in comparison to experiments which is well-known drawback of DFT. We identify the IR and Raman active modes in CSTS. The Raman modes which are a characteristic fingerprint of a structure can be used to identify the phase of CSTSwithin experiments. This communication would pave for detailed study of aiding the experimental characterization of IR, Raman, and non-linear optical properties of Cu₂SrSnS₄ paving advancements in the areas of PV and photo-electrochemical water-splitting. The nature of electronic polarization, its effect of LO/TO splitting as well as the dielectric properties can be further investigated with the present study in consideration.

Acknowledgments

Computational resources have been provided by the supercomputing facilities of the UC Louvain, Belgium (CISM/UCL) and the Consortium des Equipements de Calcul Intensif en Fede}ation Wallonie Bruxelles (CECI) funded by the Fonds de la Recherche Scientifique de Belgique (FRS-FNRS).

Funding Source

This research received no specific grant from any funding agency.

Conflict of Interest

The authors have no conflicts of interest to disclose.

References

1. A. Walsh, S. Chen, S.-H. Wei, and X.-G. Gong, Adv. Energy Mater. 2, 400 (2012)
2. W. Shockley and H. J. Queisser, J. Appl. Phys. 32, 510 (1961)
3. S. Bourdais, C. Chone, B. Delatouche, A. Jacob, G. Larramona, C. Moisan, A. Lafond, F. Donatini, G. Rey, s. Siebentritt et al., Adv. Energy Mater. 6, 1502276 (2016)
4. I. Olekseyuk, I. Dudchak, and L. Pikasch, J. Alloys Compd. 368, 135 (2004); M. Dimitrievska, A. Fairbrother, E. Saucedo, A. Perez-Rodriguez, and V. Izquierdo-Roca, Sol. Energy Mater. Sol. Cells 149, 304 (2016)
5. T. Gokmen, O. Gunawan, T. K. Todorov, and D. B. Mitzi, Appl. Phys. Lett. 103, 103506 (2013)
6. S. Chen, X. G. Gong, A. Walsh, and S.-H. Wei, Phys. Rev. B 79, 165211 (2009); C. J. Bosson, M. T. Birch, D. P. Halliday, K. S. Knight, A. S. Gibbs, and P. D. Hatton, J. Mater. Chem. A 5, 16672 (2017); J. J. Scragg, L. Choubrac, A. Lafond, T. Ericson, and c. Platzer-Bjorkman, Appl. Phys. Lett. 104, 041911 (2014)
7. F. Hong, W. Lin, W. Meng, and Y. Yan, Phys. Chem. Chem. Phys. 18, 4828 (2016)
8. D. Shin, E. Ngaboyamahina, Y. Zhou, J. T. Glass, and D. B. Mitzi, J. Phys. Chem. Lett. 7, 4554 (2016)
9. T. Zhu, W. P. Huhn, G. C. Wessler, D. Shin, B. Saparov, D. B. Mitzi, and V. Blum, Chem. Mater. 29, 7868 (2017)
10. H. Xiao, Z. Chen, K. Sun, C. Yan, J. Xiao, L. Jiang, X. Liangzin, Y. Xiaojing, and F. Liu, Thin Sol. Films 697, 137828 (2020)
11. S. P. Ramkumar, Y. Gillet, A. Miglio, M. J. van Setten, X. Gonze, and G. -M. Rignanese, Phys. Rev. B 94 224302 (2016); S. P. Ramkumar, A. Miglio, M. J. van Setten, D. Waroquiers, G. Hautier, and G. -M. Rignanese, Phys. Rev. Mater. 2, 085403 (2018); J. M. Skelton, A. J. Jackson, M. Dimitrievska, S. K. Wallace, A. Walsh, APL Mater. 3, 041102 (2015)
12. P. Hohenberg and W. Kohn, Phys. Rev. 136, B864 (1964)
13. J. Hafner, C. Wolverton, and G. Ceder, MRS bull. 31, 9 (2006)
14. J. Neugebauer, and T. Hickel, Wiley Inter. Rev: Comput. Mol. Sci. 3, 5 (2013)
15. G. R. Schleder, A. C. Padilha, C. M. Acosta, M. Costa, and A. Fazzio, J. Phys: Mater. 2, 3 (2019)
16. P. Giannozzi, S. de Gironcoli, P. Pavone, and S. Baroni, Phys. Rev. B 43, 7231 (1991); X. Gonze and C. Lee, Phys. Rev. B 55, 10355 (1997); X. Gonze, Phys. Rev. B 55, 10337 (1997)
17. G. Kresse and J. Furthmuller, Comput. Mater. Sci 6, 15 (1996)
18. P. E. Blöchl, Phys. Rev. B 50, 24 (1994)
19. J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996)
20. A. Assoud, N. Soheilnia, and H. Kleinke, Chem. Mater. 17, 2255 (2005); C. L. Teske and O. Vetter, Z. Anorg. Allg. Chem. 426, 281 (1976)
21. B. Monserrat, J-S. Park, S. Kim, and A. Walsh, Appl. Phys. Lett. 112, 193903 (2018)
22. J. Paier, R. Asahi, A. Nagiya, G. Kresse, Phys. Rev. B 79, 115126 (2009)
23. S. Chen, X. G. gong, A. Walsh, and S. H. Wei, Appl. Phys. Lett. 94, 041903 (2009)

---

This work is licensed under a Creative Commons Attribution 4.0 International License.