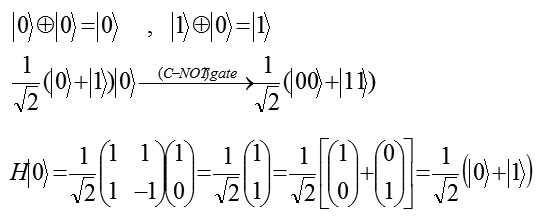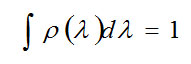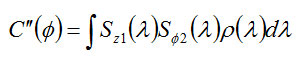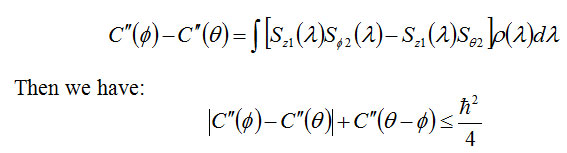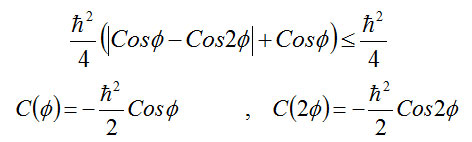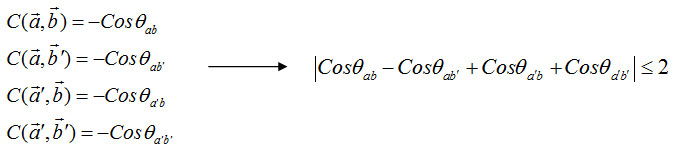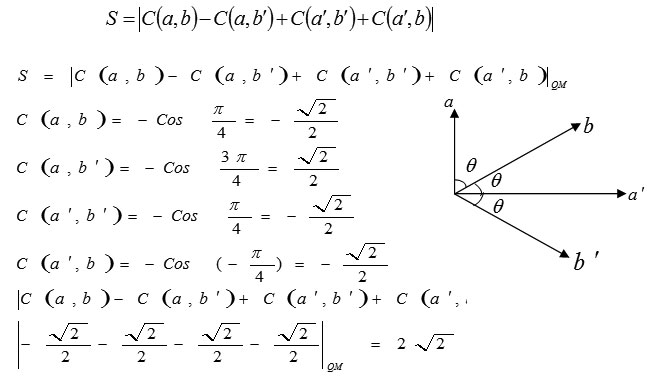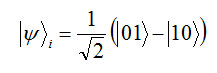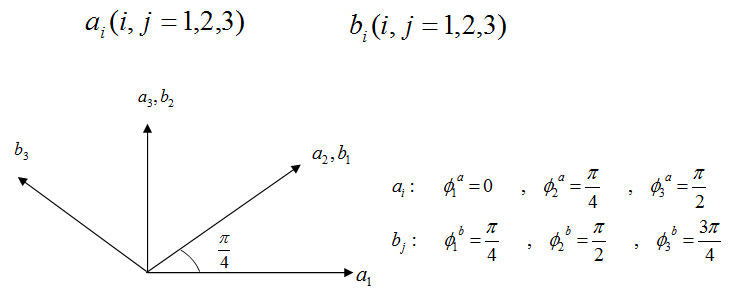Security Quantum Key Distribution in Quantum Theory Using the Theory of Bell

Yadollah  Farahmand^1,*, Zabialah Heidarnezhad² and Kh. Muminov³

^1,3Physical-Technical Institute named after S.S.Umarrov Academy of Sciences of the Republic of Tajikistan Aini Ave 299/1, Dushanbe, Tajikistan,

²Department of Chemistry, Islamic Azad University, Andimeshk , Iran

Corresponding Author Email: amirfrhmnd@gmail.com

DOI : http://dx.doi.org/10.13005/msri/100205

ABSTRACT:

Using the principles of quantum theory, quantum computers can solve the problem in encryption .We'll examine the security of quantum key distribution with Between quantum theory and relativity in the entanglement state of their validity and the generalization of  Bell's inequality and its violation .Finally, we discuss examples of quantum cryptography experiments.

KEYWORDS: Vocabulary; Quantum theory; entanglement; bell inequality; Quantum Cryptography; non locality; hidden variable

Copy the following to cite this article: Farahmand Y, Heidarnezhad Z, Muminov Kh. Security Quantum Key Distribution in Quantum Theory Using the Theory of Bell. Mat.Sci.Res.India;10(2)

Copy the following to cite this URL: Farahmand Y, Heidarnezhad Z, Muminov Kh. Security Quantum Key Distribution in Quantum Theory Using the Theory of Bell. Mat.Sci.Res.India;10(2). Available from: http://www.materialsciencejournal.org/?p=4478

Introduction

  If the two-qubit gate is applied to the output qubit is qubit entanglement.

 

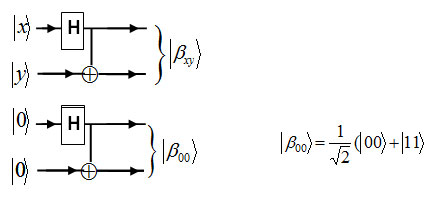
In the above circuit, the output for x = y = 0 is the two qubit state this state can not be expressed as the product of two single – qubit states and  the two qubits are said to be entangled. Note that, the two qubits are correlated in this state; they are both 0 or 1. This correlation survives even if the two qubits are separated by a large distance without disturbing the state. This sort of non-local correlation is responsible for the famous EPR(Einstein- Podolski -Rosen) paradox¹.

 

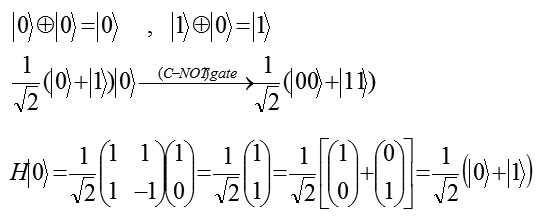
Results and Discussion

Quantum theory and relativity theory

Quantum theory does not permit no signaling because quantum theory knows a valid the theory of relativity and of causality. Otherwise, we issue the hidden local variables, which can lead to the view of Bohemian David³.

Bell in equalities

In Entanglement state once two particles are separated, the device property must be the first to measure the spin component of each particle is given. In general, it is not necessary that the hidden variable is a physical parameter of the model.

Therefore we show the measurement component Z spin S the first particle with the symbol S₁₂ (λ) the only allowable S1z values ±h/2 are and      is hidden variable. Each pair of particles has a certain amount of  λ   and the probability density  p(λ) is equal to:

 

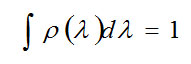
Value (expected value)  C”(Φ) for more product is:

 

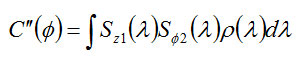
Now we consider the experimental as before the component Z First, the particle size is but this time the angle measuring the device θ The Z axis is located.

 

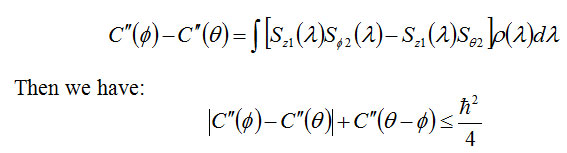
Above inequality is called Bell’s Theorem.

In the particular case θ = 2 Φ 

 

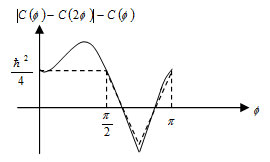
The continuous curve is based on quantum mechanics

 

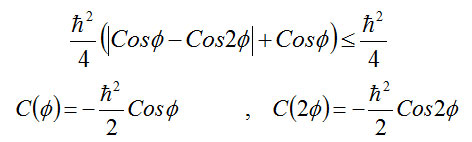
The face of Bell’s theorem shows that the range is established⁴.

Third generalized Bell inequality

This inequality of the primary structure of Bell’s theorem has been generalized and This inequality is known as unequal clouser and Shimon. This inequality works. as measured by the expected value^5,6.

 

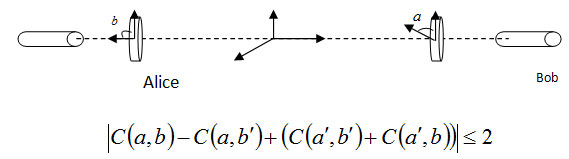
In theory, quantum mechanics can be easily generalized Bell inequalities in the third example that is being violated. Using the following relationships:

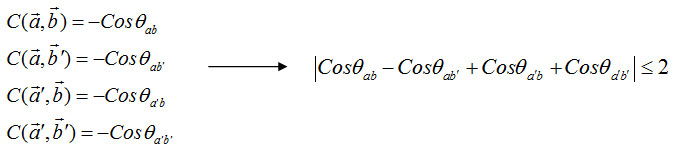
Now we assume that entanglement state |Ψ> = 1/√2(|01>+|10>) Bob and Alice are sent to the Bob and Alice can measured the direction a, a’, b, b’.

With a simple calculation can be found: θ (π/4)

 

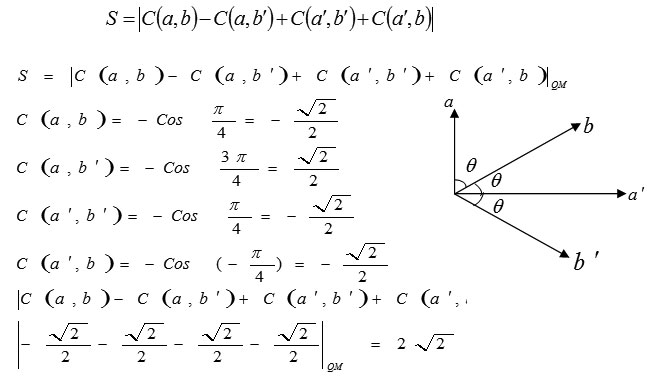
Quantum cryptographic protocols

The idea for a series of entanglement pairs of particles with spin is presented. This entanglement pair can by Alice and Bob and an eavesdropper (Eve) to be measured and evaluated. The user can easily verify this with the noise caused by the disclosure of quantum communication.

Alice and Bob share pairs of systems, each in the maximally entangled state.

 

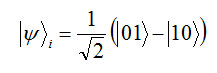
The carrier particle is entanglement qubits that separately along Axis Z two users in a channel is sent to the public.

Alice and Bob after the particles have been separated from their measurements of the spin components along the vectors b,a

and the screen is perpendicular to the direction of the particles are located.

a_i(i, j = 1,2,3)    b_i (i, j = 1,2,3)

 

 

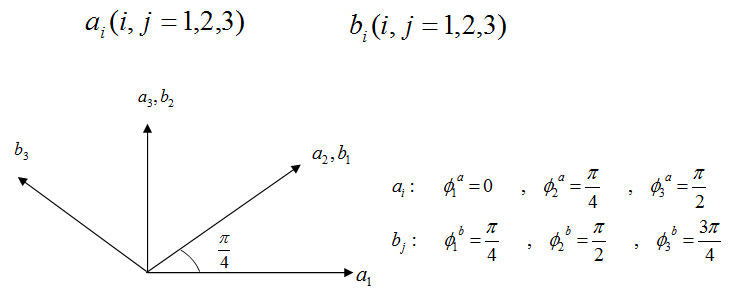
Measure their particle in the bases of users to randomly select a pair of particles can be entered; we assume: ±h/2 = ±1

When all their measurements are complete, Alice and Bob announce their bases over a public, authenticated, classical channel.

After the measurement results of the measurements are divided into two groups , the first group is the results of measurement of the two authorized users to have different uses.

the second group is the results of the two authorized user of the measurement have been used in the same direction.

Proof of Security Protocols

Quantity C(a_i, b_j) The same correlation coefficient (the expected value of measuring both the authorized user) is. On the other hand, according to quantum rules are:  C(a_i, b_j) = -a_i. b_j 

clouser and Shimon inequality is violated in quantum mechanics, quantum mechanics is the theory being that the non locale According to this idea if we can quantum key distribution protocol in the range of the theory of quantum mechanics can violate Bell’s inequality consider, if we listen to the noise created Eve to realize.

Quantity S= 2√2 

the protocol consisted of measuring the correlation coefficient, such that Alice and Bob are in a different direction.

7. Alice and Bob first results are apparent in the public channels, such as no threat to the security of the protocol does not, But it will allow the user to determine the value of S, According to the theory of quantum mechanics violate the inequality in the value of S must be equal clouser and Shimon. The security of quantum key distribution protocol confidential locality this idea in the theory of quantum mechanics is essential to. Then the authorized user on the value of their measurement results are obtained, they can be sure that the results they achieved in the second group of measurements is completely confidential and secure any eavesdropping. The results of the second qubit strings that can be confidential into key.

Conclusion

Quantum cryptography to secure communication systems can be expected to meet. Quantum theory and relativity can be entirely secure the password key exchange between users and any possible surveillance or eavesdropping can be detected by unauthorized users. The secret quantum key distribution protocol in the Bell inequality violation due to the quantum mechanical theory is non- locality it is proved safe.

References

1. A.Chatterjee.2003. Introduction to quantum computation.  quant-ph/0312111.
2. J.Perskill.2001.Lecture notes for Ph219/CS219:
3. A. Kent. 2002. Non Linearity without superluminality.quan-ph/0204106.
4. Michael a. Neilson, and Isaac L. Chuang 2003. Quantum computation and Quantum Information.
5. A.Ekert.1991. Quantum Cryptography Based on Bell’s Theory. Phys. Rev. Lett. 67. 661-663.
   CrossRef
6. G. Auletta. 2001. Foundations and Interpretation of quantum mechanics. World scientific, Singapore. New Jersey. London. Hong Kong, PP.589-607.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.