Evaluation of Dielectric Relaxation Parameters from Ionic Thermocurrent Spectrum Involving General Order Kinetics
Introduction
Thermally stimulated discharge current (TSDC) technique is ideal for the investigation of the structure of polymers, semi-crystalline polymers and co-polymers because it is a more sensitive alternative than other thermal analysis techniques for detecting the transitions that depend on changes in mobility of molecular scale structural units1-7. The technique can also be applied for the investigation of charge storage and transport processes in high resistivity materials and polymers. For many applications of polymers and doped polymers, it is necessary to know the dielectric properties of material 8. Polymer films, which can be polarized in an external electrical field, find applications as sensors sensitive to mechanical vibrations9, temperature changes or moisture10. Further application of doped materials is polymer based field effect transistor sensors11. TSDC is quite useful for the study of amorphous relaxations in polymers and their crystallizable blends. TSDC or ionic thermo current is a standard method to study dipolar defects in ionic crystals12. The basic mechanisms involved in TSDC are briefly sketched in the succeeding paragraphs.
When an alkali halide system, consisting of polarized IV dipoles in frozen-in state is heated at a constant linear heating rate, there is a stage when frozen-in polarized dipoles start depolarizing. Consequently, thermally stimulated depolarization current (TSDC) or ionic thermocurrent (ITC) starts appearing. The plot of ionic thermocurrent as a function of temperature is known as ITC spectrum.
ITC spectrum is much similar to a thermoluminescence (TL) glow curve involving first-order kinetics13. Ionic thermocurrent I as a function of temperature is expressed as13-14
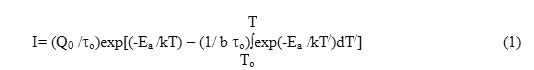
where Qo is the total charge released during ITC run and is given by

b is the constant linear heating rate according to the equation
T = To + bt (3)
In eq. (3), T represents the absolute temperature corresponding to time t and To is the temperature where from ITC curve starts to appear. In eq. (1), τo is the fundamental relaxation time or the relaxation time at infinite temperature given by Arrhenius relation as 15
τ = τo exp( Ea/ kT ) (4)
where τ is the relaxation time at T , k the Boltzmann’s constant and Ea the activation energy for the orientation of IV dipole.
The peak of the ITC spectrum appears at Tm such that
Tm2 = {(b Eaτm)/ k} (5)
where τm is the relaxation time at Tm. It has been mentioned that eq. (1) corresponds to a TL glow curve involving first order kinetics, and hence TL glow curves involving higher order kinetics may also provide corresponding equations for ITC spectra. TL glow curves involving second and higher order kinetics have already been reported in the literature16-18. Various efforts19-21 have been made by different workers for the determination of dielectric relaxation parameters from ITC spectrum involving general order kinetics, but none of them have been found to be adequate when different order of kinetics are taken into consideration.
Keeping this aim in view, mechanisms responsible for the appearance of a ITC spectra are reconsidered in this article with an aim to establish a generalized equation. Detailed methods for the determination of dielectric relaxation parameters have been discussed.
Proposed Model of Analysis
In thermo luminescence, higher order kinetics has already been reported in the literature16-18. Dwivedi et al18 has reported a new model for the occurrence of TL glow curve involving general orders kinetics. Orders of kinetics in thermo luminescence are dependent on the extent of recombination and simultaneous retrapping. Bucci, Fieschi and Guidi (BFG) method13 is usually employed to evaluate dielectric relaxation parameters Ea and τo in ITC measurements. Such evaluated values of dielectric relaxation parameters Ea and τo should satisfy eq. (5). However, it has been recorded that evaluated values of Ea and τo do not satisfy eq. (5) in general19,22. This conclusion has been obtained at by Prakash and Nishad22, while developing characteristic relaxation time for a lattice dopant system.
Thus it has been observed that Eq. (5) is not adequate enough to explain the location of ITC spectrum of actual experimental systems. Keeping discussions of preceding paragraphs in view and in the light of the outcome of the model suggested by Dwivedi et al18 for TL glow curve involving general orders kinetics, a new model has been developed for the occurrence and analysis of ITC spectrum.
ITC spectrum
The thermally stimulated depolarization current density J depends on the rate of depolarization of IV dipoles and can be expressed as
J = (-1/ℓ)dP(t)/dt (6 )
It has been found that the rate of depolarization depends on the remaining polarization P present at that time and on the relaxation time τ. In the present work it is proposed that the rate of depolarization also depends on the order of kinetics. Thus, the rate of depolarization can be expressed as
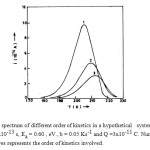
d P(t)/dt = (-1/ℓ)[P(t) / t] (7)
where ℓ is the order of kinetics involved in the system.
Eqn. (6) and (7) can be combined to have
J=(1/ℓ2)[P(t)/t] (8)
Eqn.(7) after integration gives
P(t) = Po exp [(-1/ℓ) (t / t) ] (9)
where Po is the maximum polarization. P0 depends on polarizing electric field Ep and polarization temperature Tp as
Po = [αNd μ2 Ep / k Tp ] (10)
where Nd is the number of IV dipoles per unit volume each with dipole moment m, k the Boltzmann constant and a the geometrical parameter which for freely rotating dipoles has a value 1/3 (a equals to 2/3 for nn face centered vacancy positions in ionic crystals).
Eqn.(8) with help of eqns. (9) results into
J(t) = [(1/ℓ2) P(t) /t]
= (1/ℓ2)(Po/t) exp[-(1/ℓ)t /t] (11)
Non-isothermal form of eqn. (11) for the decay of polarization will be
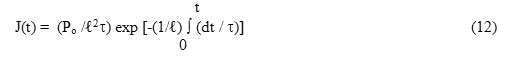
where time is measured from the very appearance of the depolarization current after switching off the electric field. Use of the Arrhenius relation {eqn. (4)}, changes eqn.(12) into
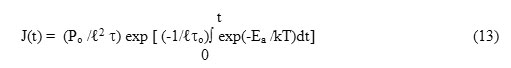
If the system is heated following a constant linear heating rate b as per eqn. (3). Then, eqn. (13) with the help of eqn.(3) can be re-arranged as
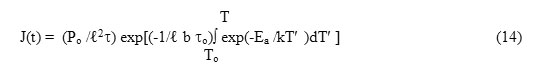
With the help of eqns.(1) and (14), one can write down the expression for the depolarization current i (T) as
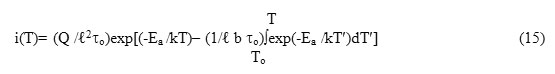
where Q is the total charge released in the ITC measurement and is related to P0 through the relation
Q = Po A = [αNd μ2 Ep A /k Tp ] (16)
where A is the cross sectional area of the crystal specimen.
Equation (15) is the generalized equation for ITC spectrum involving ℓ th order of kinetics. Thus, it is obvious that one can have ITC spectra involving higher-order kinetics using eq. (15) after substituting the corresponding values of ℓ into it.
Some typical ITC curves as per eqn. (15) for different order of kinetics are shown in Fig. 1.
Figure1: ITC spectrum of different order of kinetics in a hypothetical system with to = 2.5×10-13 s, Ea = 0.60 , eV., b = 0.05 Ks-1 and Q =3×10-11 C. Number on the curves represents the order of kinetics involved.
Condition for the Peak of the ITC Spectrum
The condition for the occurrence of the peak of the ITC spectrum is obtained after differentiating eqn.(8) with respect to t and using eqn.(6) as
[(dJ/dt) t + J (dt/dt)] = (- J/ℓ) (17)
on putting the condition of maximum depolarization current in the ITC spectrum i.e. (dJ/dt)=0, we have from eqn. (17)
[ (dt
m/dt) + (1/ℓ)] J = 0
which suggest that either
[(dt
m/dt)+ (1/ℓ)] = 0 or J = 0
Since J can not be equal to zero in the range of temperature where ITC spectrum is recorded, so it is obvious that
[(dt
m/dt) + (1/ℓ)] = 0
this condition in combination with Arrhenius relation {eqn. (4) } gives
Tm2 = [ℓb Eatm / k] =(ℓto) (b Ea / k) exp[Ea / k Tm] (18)
where Tm is the temperature at which maximum current im in the ITC spectrum appears and tm is the corresponding relaxation time at Tm. The values of Tm for different hypothetical systems are presented in table 1. It is obvious that Tm changes appreciably with a change in ℓ. Table 1 suggests that Tm remains unchanged for the same value of ℓt0 in accordance with eqn. (18). Such a situation however, does not pose any problem in the evaluation of dielectric relaxation parameters. It is obvious from eqn.(18) that Tm is independent of Q and hence also of Nd as expected and appears to be at same location if b is kept fixed.
Table1: Tm for ITC Spectra for different sets of Ea, ℓ and to
|
Ea
(eV)
|
to
(s)
|
Tm FOR (K)
|
|
ℓ = 1
|
ℓ = 2
|
ℓ = 3
|
|
0.50
|
1.0 x 10-13
|
168
|
171
|
173
|
|
0.50
|
2.5 x 10-13
|
173
|
176
|
178
|
|
0.50
|
5.0 x 10-13
|
176
|
180
|
182
|
|
0.55
|
1.0 x 10-13
|
185
|
188
|
190
|
|
0.55
|
2.5 x 10-13
|
189
|
193
|
195
|
|
0.55
|
5.0 x 10-13
|
193
|
197
|
199
|
|
0.60
|
1.0 x 10-13
|
201
|
205
|
207
|
|
0.60
|
2.5 x 10-13
|
206
|
210
|
212
|
|
0.60
|
5.0 x 10-13
|
210
|
214
|
217
|
|
0.65
|
1.0 x 10-13
|
217
|
221
|
224
|
|
0.65
|
2.5 x 10-13
|
223
|
227
|
230
|
|
0.65
|
5.0 x 10-13
|
227
|
232
|
234
|
|
0.70
|
1.0 x 10-13
|
233
|
238
|
240
|
|
0.70
|
2.5 x 10-13
|
239
|
244
|
247
|
|
0.70
|
5.0 x 10-13
|
244
|
249
|
252
|
Evaluation of Dielectric Relaxation Parameters
From eqn.(6) one gets
i(t) = (-1 /ℓ)dQ /dt (19)
Eqn.(19) after integration, can be rearranged as

and

If the system is heated as per eqn.(3) following a constant linear heating rate b, eqn.(21) changes as
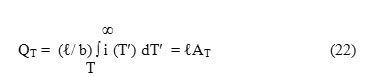
where QT is the number of released charge carriers per unit volume at the temperature T corresponding to time t and AT represents the area of the ITC spectrum enclosed within the temperature range T to ∞ such that
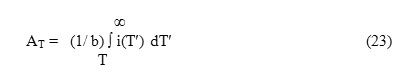
Further eqn.(20) can also be represented as
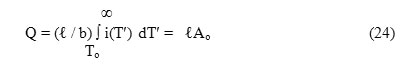
where Ao represents the total area enclosed within the ITC spectrum such that
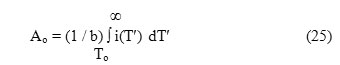
Rearrangement of eqns.(11), (16) and (22), gives
XT = ( ℓto )exp(Ea /kT) (26)
where
XT = AT / i(T) (27)
Eqn.(26) can further be written as
ln (XT)= ln ( ℓto ) +(Ea /kT) (28)
For a given ITC curve of a system, ℓ, to and Ea are constant, so the plot of ln (XT) vs (1/T) will be a straight line with the slope (Ea /k) and intercept equal to ln(ℓto). Such straight line plots in ln(XT) vs (1/T) corresponding to Fig.1 is shown in Fig. 2.
Figure2: Variation of ln [XT] Vs [1/T] for different order of kinetics in a hypothetical system with t0 = 2.5×10-13 s, Ea = 0.60 eV., b = 0.05 Ks-1 and Q =3×10-11 C. Number on the curves indicates the order of kinetics.
Thus, the activation energy can be evaluated from the slope of the straight line plot. The intercept gives the value of either ℓ or to provided the other is known. In order to evaluate the order of kinetics involved we have calculated the value of the form factor g = (Tm/ (T2–Tm)) similar to the case of TL processes18. The calculated values of form factor for different sets of Ea ,to and ℓ are listed in table 2.
Table2: Form factor for ITC spectra for different sets of Ea, ℓ and to
|
Ea
(eV)
|
to
(s)
|
Form Factor y = [Tm /(T2-Tm)]
|
|
ℓ = 1
|
ℓ = 2
|
ℓ = 3
|
|
0.50
|
1.0 x 10-13
|
30.54
|
29.70
|
28.38
|
|
0.50
|
1.5 x 10-13
|
30.90
|
29.69
|
28.40
|
|
0.50
|
2.0 x 10-13
|
30.20
|
29.16
|
28.36
|
|
0.50
|
2.5 x 10-13
|
30.14
|
29.33
|
28.52
|
|
0.50
|
3.0 x 10-13
|
30.14
|
29.50
|
28.68
|
|
0.50
|
3.5 x 10-13
|
30.31
|
29.60
|
28.48
|
|
0.50
|
4.0 x 10-13
|
30.48
|
29.66
|
28.48
|
|
0.50
|
5.0 x 10-13
|
30.66
|
29.34
|
28.40
|
|
0.50
|
6.0 x 10-13
|
30.84
|
29.43
|
28.15
|
|
0.55
|
1.0 x 10-13
|
30.38
|
29.29
|
28.48
|
|
0.55
|
1.5 x 10-13
|
30.05
|
29.23
|
28.47
|
|
0.55
|
2.0 x 10-13
|
30.12
|
29.53
|
28.70
|
|
0.55
|
2.5 x 10-13
|
30.28
|
29.69
|
28.39
|
|
0.55
|
3.0 x 10-13
|
30.44
|
29.48
|
28.00
|
|
0.55
|
3.5 x 10-13
|
30.60
|
29.42
|
28.64
|
|
0.55
|
4.0 x 10-13
|
30.76
|
29.07
|
28.28
|
|
0.55
|
5.0 x 10-13
|
30.50
|
29.22
|
28.42
|
|
0.55
|
6.0 x 10-13
|
30.48
|
29.37
|
28.57
|
|
0.60
|
1.0 x 10-13
|
30.75
|
29.28
|
28.58
|
|
0.60
|
1.5 x 10-13
|
30.11
|
29.57
|
28.58
|
|
0.60
|
2.0 x 10-13
|
30.40
|
29.58
|
28.13
|
|
0.60
|
2.5 x 10-13
|
30.55
|
29.00
|
28.26
|
|
0.60
|
3.0 x 10-13
|
30.70
|
29.13
|
28.53
|
|
0.60
|
3.5 x 10-13
|
30.58
|
29.27
|
28.66
|
|
0.60
|
4.0 x 10-13
|
30.40
|
29.41
|
28.66
|
|
0.60
|
5.0 x 10-13
|
30.00
|
29.35
|
28.02
|
|
0.60
|
6.0 x 10-13
|
30.14
|
29.60
|
28.15
|
|
0.65
|
1.0 x 10-13
|
30.27
|
29.46
|
28.00
|
|
0.65
|
1.5 x 10-13
|
30.37
|
29.68
|
28.25
|
|
0.65
|
2.0 x 10-13
|
30.51
|
29.19
|
28.50
|
|
0.65
|
2.5 x 10-13
|
30.70
|
29.31
|
28.75
|
|
0.65
|
3.0 x 10-13
|
30.90
|
29.45
|
28.02
|
|
0.65
|
3.5 x 10-13
|
30.00
|
29.57
|
28.14
|
|
0.65
|
4.0 x 10-13
|
30.13
|
29.70
|
28.26
|
|
0.65
|
5.0 x 10-13
|
30.26
|
29.00
|
28.39
|
|
0.65
|
6.0 x 10-13
|
30.40
|
29.12
|
28.63
|
|
0.70
|
1.0 x 10-13
|
30.10
|
29.75
|
28.23
|
|
0.70
|
1.5 x 10-13
|
30.48
|
29.11
|
28.58
|
|
0.70
|
2.0 x 10-13
|
30.70
|
29.36
|
28.82
|
|
0.70
|
2.5 x 10-13
|
30.68
|
29.60
|
28.24
|
|
0.70
|
3.0 x 10-13
|
30.00
|
29.72
|
28.36
|
|
0.70
|
3.5 x 10-13
|
30.25
|
29.48
|
28.47
|
|
0.70
|
4.0 x 10-13
|
30.24
|
29.05
|
28.59
|
|
0.70
|
5.0 x 10-13
|
30.50
|
29.29
|
28.00
|
|
0.70
|
6.0 x 10-13
|
30.62
|
29.41
|
28.11
|
|
Average Value of form Factor
|
30.41
|
29.40
|
28.39
|
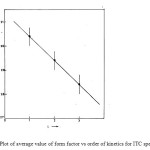
From the table 2 it is clear that the average value of form factor for first order kinetics is 30.41 and for second order kinetics it is 29.40 and for third order kinetics it is found to be 28.39. To have the value of form factor γ justified for systems involving different order of kinetics 135 hypothetical systems have been considered in table 2. It should be mentioned that form factor γ for the systems involving first order kinetics as obvious from tables 2 lies in the range 30.00 ≤ γ ≤ 30.90, and that for systems involving second order kinetics it lies in the range 29.00 ≤ γ ≤ 29.75
whereas for systems involving third order kinetics it is found to lie in the range 28.00 ≤ γ ≤ 28.82. A graph plotted between the average values of the form factor vs order of kinetics is shown in Fig 3.
Figure3: Plot of average value of form factor vs order of kinetics for ITC spectrum.
From this curve, for a known value of form factor corresponding to an experimental ITC spectrum of a system, the order of kinetics involved can be ascertained. It should be noted that no overlapping values of form factor is obtained corresponding to different order of kinetics. The value of ℓ can also be determined using eqn.(24), if the value of Nd is known through some other independent experiment. Once the order of kinetics is known, the relaxation time can be evaluated from the intercept of the straight line plot drawn in accordance with eqn. (28). Thus the dielectric relaxation parameters Ea, ℓ and to can be evaluated in systems involving different order of kinetics.
Results and Discussion
The proposed model is free from all the anomalies discussed in the introduction section. A generalized equation is developed which is capable of explaining the occurrence and analysis of ITC spectrum involving different order of kinetics. While analyzing the ITC data reported in the literature 22, it has been found that eq. (5) is not satisfied. The values of dielectric relaxation parameters Ea and τo are evaluated ussing BFG method13 and are reported as such without taking care of eq. (5). However, It is essential that the evaluated values of Ea and τo must satisfy eq. (5). This aspect has not been considered by many researchers working in ITC studies. Keeping above facts in view a generalized equation has been developed which is capable of explaining the ITC spectrum involving different order of kinetics including first order. The anomalies associated with the eq. (5) have been removed through eqn. (18). Eqn. (18) for Tm gives the location of peak of ITC spectrum for different order of kinetics including first order. Figure 1 reveals that, peak position Tm shifts to higher temperature with a simultaneous decrease in the peak of the ITC spectrum im with increasing values of ℓ . It is obvious that change is more pronounced, when one goes from ℓ = 1 to ℓ = 2, which further decreases with increase in the value of ℓ. The nature recorded in figure 1 is found to be in good agreement with eqs (15) and (18).
From factor g is found to be different for different ℓ. No overlapping values of g is found for different ℓ. Dielectric relaxation parameters are evaluated using straight line plots and hence errors if any during evaluation procedure are averaged out.
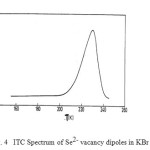
To seek acceptability and reliability of the proposed model it has been applied to a number of experimental systems whose ITC spectra are available in the literature. Experimental data of ITC spectra for a good number of systems have been utilized to evaluate the dielectric relaxation parameters following the suggested method of analysis. As a representative case suggested model has been applied to experimentally observed ITC spectra of KBr: Se2- system23 which is shown in Fig. 4. The variation of ln (XT) vs (1 / T) for KBr: Se2- system is shown in Fig.5.
Figure4: ITC Spectrum of Se2- vacancy dipoles in KBr system.
Figure5: Plot of ln [XT] Vs [1/T] for KBr: Se2- system.
Evaluated dielectric relaxation parameters are presented in table 3. It is obvious from table 3 that there is good agreement in between reported and evaluated values of dielectric relaxation parameters.
Table3: Reported and evaluated values of dielectric relaxation parameters for KBr: Se2- system.
|
Reported
|
Evaluated
|
|
b(Ks-1)
|
ℓ
|
Ea (eV)
|
τo (s)
|
Form factor
|
ℓ
|
Ea (eV)
|
τo (s)
|
|
0.050
|
1(presumed)
|
0.720
|
2.00×10-14
|
30.60
|
1
|
0.718
|
1.99×10-14
|
It is worth mentioning that the KBr: Se2- system involves first order kinetics. Thus with the help of suggested model, one can evaluate successfully dielectric relaxation parameters namely activation energy Ea , fundamental relaxation time τo , order of kinetics ℓ and approximate number of dipoles per unit volume.
Conclusion
A generalized equation has been developed to explain the mechanisms responsible for the occurrence of the ITC spectrum involving different order of kinetics. Methodology has been developed to evaluate the dielectric relaxation parameters. The proposed model has been applied to number of experimental systems and it has been found that there is good agreement in between reported and evaluated values of dielectric relaxation parameters.
Acknowledgement
Author is thankful to Prof. R. Chen (Tel Aviv, Israil) and Prof. Jai Prakash, Ex Head, Department of Physics, D.D.U. Gorakhpur University, Gorakhpur for valuable suggestions during preparation of the manuscript.
References
- Ikezaki, Fujite K , Wada I and Nakamura K J, J Electrochem Soc , 121, 591 (1974).
CrossRef
- Perlman M M , J Electrochem Soc, 119, 892(1972).
CrossRef
- Wintle H J and Pepin M P , J of Electrostat, 48, 115 (2000).
CrossRef
- Matsui K, Tanaka Y, Takada T, Fukao T, Fukunaga K, Maeno T and Alison J M, IEEE Dielectr Electr Insul , 12, 406 (2005).
CrossRef
- Lee KY, Lee K W, Choi Y S, Park D H and Lim K J, IEEE Dielectr Electr Insul ,12, 566 (2005).
CrossRef
- Burghate P K, Deogaonkar V S, Sawarkar S B, Yawale S P and Pakade S V, Bull Matter Sc, 26, 267 (2003).
CrossRef
- Robert R, Barboza R, Ferreira G F L and Ferreira de Souza M , Phys Stat Sol, b 59, 335 (2006).
CrossRef
- Reichmanis E, Ober C K, McDonald S, Iwaynagi T and Nishikubo T, (Eds.) Microelectronics Technology: Polymers in Advanced Imaging and Packaging, American Chemical Society Symposium Series, 614(1995).
- Yu S, Hing P and Hu X, J Appl Phys, 88, 398 (2000).
CrossRef
- Ploss B, Shin F G , Chan H L W and Choy C L, Appl Phys Lett, 76, 2776 (2000).
CrossRef
- Patel K S, Kohl P A and Allen S A B, J Polymer Sc B Polymer Physics,38, 1634 (2000).
CrossRef
- Bucci C and Fieschi R, Phys Rev Letters, 12, 16 (1964).
CrossRef
- Bucci C, Fieschi R and Guidi G, Phys Rev, 148, 816 (1966).
CrossRef
- McKeever S W S , Thermoluminescence of Solids, Cambridge University Press, Cambridge (1988).
- Arrhenius S Z, Z Phys Chem, 4, 226 (1889).
- Basun S, Imbusch G F, Jia D D and Yen W M, J lumen, 104, 283 (2003).
- Prakash J, Solid State Comm, 85, 647 (1993).
CrossRef
- Dwivedi D K and Prakash J, Proc Nat Acad Sci India Sect A, 80, 153 (2010).
- Prakash J , Pramana J Physics, 80, 143 (2010).
CrossRef
- Neagu R M and Neagu E R , J Opto Electronics Adv Mat., 8, 949 (2010).
- Ahemad M T, J Korean Physical Society, 57, 272 (2010).
CrossRef
- Prakash J and Nishad A K , Japn J Appl Phys, 27, 2247 (1988).
CrossRef
- Prakash J, J Phys, C12, L577 (1979).
Views: 299
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Material Science Research India An International Peer Reviewed Research Journal
Material Science Research India An International Peer Reviewed Research Journal


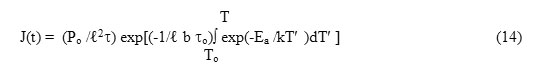
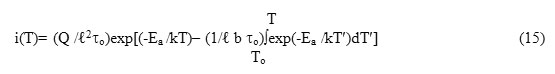


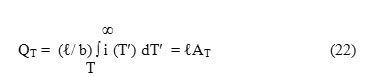
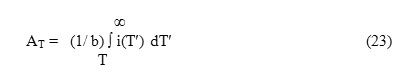
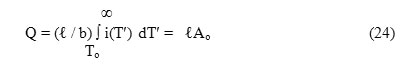
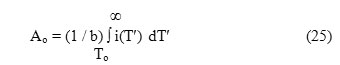
![Fig. 2 Variation of ln [XT] Vs [1/T] for different order of kinetics in a hypothetical system with 0 = 2.5x10-13 s, Ea = 0.60 eV., b = 0.05 Ks-1 and Q =3x10-11 C. Number on the curves indicates the order of kinetics.](http://www.materialsciencejournal.org/wp-content/uploads/2015/06/Vol12_No1_Eval_D.K_fig2-150x150.jpg)
![Fig. 5 Plot of ln [XT] Vs [1/T] for KBr: Se2- system.](http://www.materialsciencejournal.org/wp-content/uploads/2015/06/Vol12_No1_Eval_D.K_fig5-150x150.jpg)

