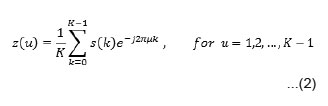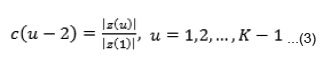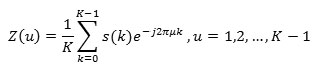Wael M. Khedr and Qamar A. Awad
Department of Mathematical, Faculty of Science, Zagazig University, Egypt.
DOI : http://dx.doi.org/10.13005/msri/080206
Article Publishing History
Article Received on : 10 Aug 2011
Article Accepted on : 17 Sept 2011
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:
In this paper, we develop a simple three layered neural network for recognition the invariant contour of image. Our approach relies on a method which normalizes the Fourier Descriptors (FDs) of image contour with its Laplace transform. Our approach is inspired the observations that the traditional Fourier transform of a 1-D is equivalent to the 2-D of image recognition. We compare between them throughout their efficient recognition.
KEYWORDS:
Neural Network; Fourier Descriptor; Laplace Transform; image contour
Copy the following to cite this article:
Khedr W. M, Awad Q. A. Study of Fourier Descriptors and It?S Laplace Transform for Image Recognition. Mat.Sci.Res.India;8(2)
|
Introduction
A supervised learning process of artificial neural networks is the machine learning task of inferring a function from supervised training data. The Backpropagation algorithm is one of the simpler members of a family of training algorithms collectively termed gradient descent. The idea is to minimize the network total error by adjusting the weights by backpropagation learning process.1
The task of image pattern recognition in real-time is a difficult one. One of the most critical steps is the process of feature extraction. Usually one has to choose a compromise among certain characteristics such as invariability, discriminating powers, dimensionality and computational complexity of the feature set. Invariant features have the strength of keeping the same value despite geometric transformations (rotation, scaling, and translation). A Fourier transform7 is the most one important transformation function to extract the invariant rotation, scaling, and shift features.
Fourier descriptors (FD) provide one method which can be used to describe the boundaries of no overlapping objects. This method possesses the added advantage of producing a representation that is invariant with respect to rotation, translation, and scale changes.3 We computed the Fourier descriptor and its Laplace transform of the image contour.
Fourier Descriptors and Laplace Transform
Fourier analysis is a fundamental tool in mathematics, signal and image processing. The discovery, popularization, and digital realization of fast algorithms for Fourier analysis (FFT) have had far reaching implications in science and technology in recent decades. The scientific computing community regards the FFT as one of the leading algorithmic achievements of the 20th century.3 In fact, even ordinary consumer-level applications now involve FFT’s think of web browser decoding JPEG images so that development of new tools for Fourier analysis of digital data may be of potentially major significance.
Given a close shape in a 2D Cartesian plane, the boundary s of the image can be traced and re-sampled according to, say, the counterclockwise direction, to obtain an uniformly distributed K points . Each point’s coordinates can be expressed as (x0,y0), (x1, y1), (x2, y2),…, (xK-1,yK-1). These coordinates can be expressed in the format of x(k) = xk and y(k)= yk . Under this condition, the boundary can be expressed as a sequence of complex numbers:
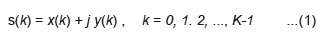
That means the x-axis is treated as the real axis and the y-axis as the imaginary axis. The coefficients of Discrete Fourier Transform (DFT) of this complex sequence z(u) is:
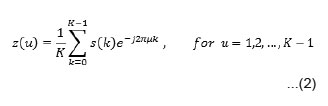
The complex coefficients z(u) are called the Fourier descriptors of the boundary. Fourier Descriptors are not directly invariant to image transformations including scaling, translation and rotation, but the changes in the parameters can be related to simple operations on the Fourier descriptors [3]. To get rid of the components caused by scaling, translation, rotation and starting point, we can use equation (3) to keep the Fourier descriptors invariant to scaling, translation, rotation and starting point.
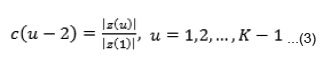
Algorithm of Fourier Descriptor and its Laplace Transform
Step 1
Convert the grayscale image matrix into black and white.
Step 2
Evaluate the edge detection of black and white image.
Step 3
Given a close shape in a 2D Cartesian plane into the edges of image, the boundary S of the shape can be traced and re-sampled according to the counterclockwise direction xy-plan of point (x,y): S(k)=x(k)+iy(k) , k = 1,2,…,K-1 ; that means the x-axis is treated as the real axis and the y-axis as the imaginary axis.
Step 4
Compute the Fourier Descriptor (FFT) of edge detection S.
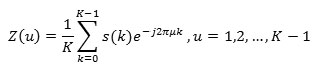
Step 5
Compute the Laplace transform of edge detection as:
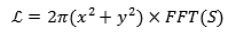
where: FFT(S) is Z (u).
Step 6
We have been made a comparison between Fourier Descriptor and Laplace Transform.
Artificial Neural network
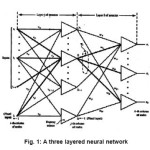
We constructed a three layered neural network for image recognition as show in figure (1). The Backpropagation algorithm has been used for training process of artificial neural networks [1,9].
Figure 1: A three layered neural network
Applications
Handwritten Characters
We display nine different shapes of three handwritten characters ‘a’, ‘b’ and ‘c’ as in figure (2). We determine their quantization contour as in figure (3), and applied the Fourier Descriptors and its Laplacian transform as in figure 4
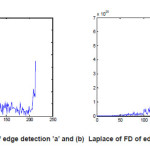
In Figure (4.a) and (4.b) we deducted that the Laplace Transform is very compact feature of edge than Fourier Descriptor as shown in these figures, and the values from 0 to 50 at x-axis tend to 0.
Figure 2: Hand written characters ‘a’, ’b’ and ‘c’ picture
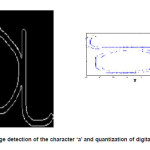
Figure 3: Edge detection of the character ‘a’ and quantization of digital edge
Figure 4: (a) F.D. of edge detection ’a’ and (b) Laplace of FD of edge detection ‘a’
Image Faces
We also display a five faces of image as in figure 6, and we applied Fourier Descriptor FD of the edges and its Laplace as in figure 8.
Figure 6: Images of five faces
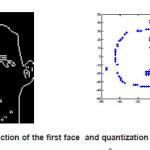
Figure 7: Edge detection of the first face and quantization of digital edge
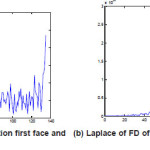
Figure 8: (a) F.D. of edge detection first face and (b) Laplace of FD of edge detection of first face
Conclusion
We used Fourier descriptors FD with Laplace transform to extract the invariant features of patterns in our approach, we applied FD of the edges of the images. We deduced that the FD of the edges of images with low details as three different characters of ‘a’, ‘b’, and ‘c’ and five faces of image examples is very good. Also, the Laplace transform, of FD is very compact feature than Fourier Descriptor.
References
- Zurada, Jacek, M. “Introduction to artificial neural systems,” St. Paul, New York (1992).
- A. L.C. Barczak, M. J. Johnson, C. H. Messom, “Revisiting Moment Invariants: Rapid Feature Extraction and Classification for Handwritten Digits,” Proceedings of Image and Vision Computing, pp. 137–142, Hamilton, New Zealand, (2007).
- MacQueen, J.B., “Some methods for classification and analysis of multivariate observations,” In: Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability, 1. University of California Press, Berkeley, CA, pp. 281–297 (1967).
- B. Lerner, H. Guterman, M. Aladjem, and I. Dinstein, “A Comparative Study of Neural Network Based Feature Extraction Paradigms,” Pattern Recognition Letters 20(1): 7-14 (1999).
CrossRef
- Y. Le Cun, B. Boser, J.S. Denker, D. Henderson, R.E. Howard, W. Hubbard, and L.D. Jackel, “Backpropagation Applied to Handwritten Zip Code Recognition,” Neural Computation, 1: 541-551 (1989).
CrossRef
- Xu, L., Ying-Yang Machine: “A Bayesian– Kullback scheme for unified learning and new results on vector” (1995).
- Qing Chenl, Emil Petriul, and Xiaoli Yang, “A Comparative Study of Fourier Descriptors and Hu’s Seven Moment Invariants for Image Recognition,” CCECE 2004- CCGEI 2004, Niagara Falls, May 2004 0-7X03-X253-6/04/ $17.00 2004 IEEE
- C. Kim, C.-H. Choi , “Image covariance-based subspace method for face recognition,” Pattern Recognition 40: 1592-1604 (2007).
CrossRef
- Tsypkin, Ya. Z. “Foundations of the Theory of Learning Systems,” NewYork: Academic press, (1973).

This work is licensed under a Creative Commons Attribution 4.0 International License.
 Material Science Research India An International Peer Reviewed Research Journal
Material Science Research India An International Peer Reviewed Research Journal