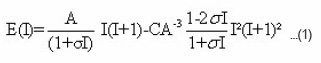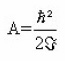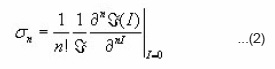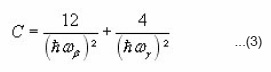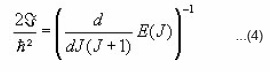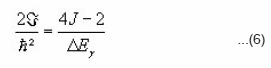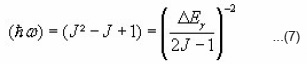Systematic Analysis of Rotational Bands for Medium and Heavy Nuclei

Hossam M. Algebaly

Physics Department, Faculty of Science, Cairo University (Egypt). Umm Al-Qura University, University College, Makkah Al-Mukarramah, Kingdom of Saudi Arabia ,

DOI : http://dx.doi.org/10.13005/msri/080202

ABSTRACT:

The systematic analysis of rotational bands for medium and heavy nuclei (covering the mass region from 100 to 244) has been studied through the theoretical model, the variable moment of inertia with softness (VMIS),and the experimental data. This model used to investigate the behavior of backbending and upbending in nuclear moment of inertia. A systematic study of the level structure up to spin 20⁺ of the selected nuclei including soft as well as good rotors and exhibit back bending or up bending are performed. Good agreement between the theoretical model and the experimental data are observed.

KEYWORDS: Rotational bands; Rare earth and actinide nuclei; Backbending behavior

Copy the following to cite this article: Algebaly H. M. Effects of Geometrical Cross- Section on Fatigue Strength of Aluminum Alloy (6063). Mat.Sci.Res.India;8(2)

Copy the following to cite this URL: Abu-Ein S. Q, Al-Marahleh G. S, Fayyad S. M. Effects of Geometrical Cross- Section on Fatigue Strength of Aluminum Alloy (6063). Mat.Sci.Res.India;8(2). Available from: http://www.materialsciencejournal.org/?p=2617

Introduction

The variable moment of inertia with softness (VMI) model^1,2 and its phenomenological equivalent, the cranking model³, have been generally accepted as given very good descriptions of ground state bands, and also β and γ bands, of even-even nuclei up to the point where the backbending occurs. Earlier works in this direction^4-7 use the same set of VMI parameters for both the ground state band and the superband, which does not seem justified. Since it has been experimentally found that the moment of inertia of the nucleus after the backbending point remains almost constant, suggesting superband of purely rotational nature.⁸

The effect of backbending occurs due to the rapid increase of the moment of inertia with rotational frequency towards the rigid value.⁹ When the rotational energy exceeds the energy needed to break a pair of nucleon, the unpaired nucleon goes into different orbits, which result in change of the moment of inertia.¹⁰

An explanation of this effect is due to a disappearance of the pairing correlation^11-12 by the action of Coriolis force, where the nucleus then undergoes a phase transition from a superfluid state to a state of independent particle motion

In this paper , we have able to study different phenomena in all known cases in medium and heavy even-even nuclei, i.e) in the Pd region, the Ba-Ce region, the rare earth region, and Pu²⁴⁴ which lie in the actinide region. In this analysis we calculate the value of R₄ ¹³, the softness S¹⁴, and study the backbending phenomena. In the next section the propsed formula is given. In last section numerical calculations and discussions are presened.

Formation

In present work we use the variable moment of inertia with softness VMIS.¹⁵ We have calculated the energy levels in ground state rotational band of deformed nuclei using the form

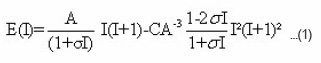
Where

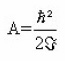
And the softness parameter σ is given by¹⁶

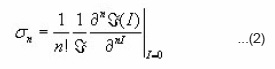
Where ℑ being the unperturbed nuclear moment of inertia,¹⁷ and the constant C is connected with β – and γ- vibrational energies through the relation¹⁸

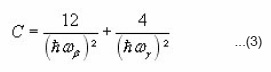
Here hω_β and hω_γ are the head energies of these vibrations, respectively. However, since the experimental data on β- and γ– vibrational bands head energies of deformed doubly even nuclei is incomplete, we take A , σ and C as free parameters of the VMIS model, which are adjusted by minimizing equation (1) to give a least square fit to experiments for low and high angular momentum.

We next perform a comparative study between our calculations and the experimental data, through the ℑ and ω² plots. The moment of inertia ℑ and ω² square rotational frequency are related to the spin derivative of the energy¹⁹

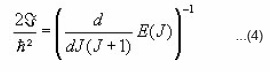
respectively, we then employ equations (2) and (3) to deduce the most sensitive relations expressive of ℑ and ω², respectively, given

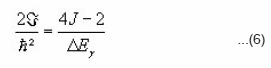
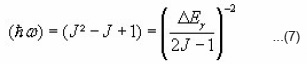
Where

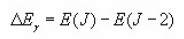
Results and Discussion

Using the formalism of sec.II and the experimental data, we have able to study different phenomena in all known cases in medium and heavy even-even nuclei, i.e) in the Pd region, the Ba-Ce region, the rare earth region, and Pu²⁴⁴ which lie in the actinide region. In this analysis we calculate the value of R₄¹³, the softness S¹⁴, and study the backbending phenomena.

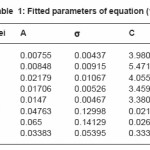
The corresponding parameters A, σ and C of equation (1) are listed in table 1.

Table 1: Fitted parameters of equation (1)

Click on image to enlarge

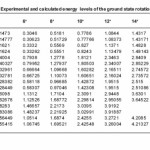
Table 2: Experimental and calculated energy levels of the ground state rotational band

Click on image to enlarge

The studied nuclei are shown as points on an N vs Z plot, figure (1).

The corresponding parameters A , σ and C of equation (1) are listed in table (1).

It will be turned out that the VMIS model give good results and will be compared with the experimental²⁰ data through the relation between E vs I(I+1) as shown in figures (2-9) and table (2).

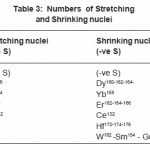
The softness S of these nuclei indicates that the rotational nuclei are very close to each other. The rotational nuclei are divided into two groups, stretching nuclei, with positive S value, as soft rotors and shrinking nuclei, with negative S value, as hard rotors, table (3).

Table 3: Numbers of Stretching and Shrinking nuclei

Click on image to enlarge

The nuclei in our  investigation can be divided into three groups according to the value of R4 , where

Region(I) : 2 ≤ R4 ≤ 2.4, for vibration nuclei,(e.g.) Ba140…

Region(II) : 2.4 ≤ R4 ≤ 3, for transitional nuclei,(e.g.) Zr100, Pd110, Xe122,…

Region(III) : 3 ≤ R4 ≤ 10/3, for rotational nuclei,(e.g.) Dy160, Er162, Yb164, Gd158,…

For our calculations of the softness S and R₄ it is clear that most of the nuclei under investigation(e.g. more than 30 nuclei) lie in the rotational region.

The relation 

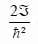
(Mev-1) vs.

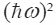
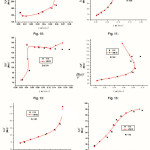
(Mev2) backbending plots are given for six nuclei. The figures include nuclei which show explicit backbending in the yarst band (Pu²⁴⁴, Er¹⁶²) and nuclei showing explicit backbending in the β band (Gd¹⁵⁴) and nuclei exhibiting just upbending in the yarstband (Yb¹⁶⁸). The theoretical model and the experimental data used in each case is shown in the figure caption (10-15).

Figure (2-9): Shows the relation between rotational energy E and angular momentum I(I+1) for Pu²⁴², Th²³², Os¹⁸², Er¹⁶², Dy¹⁶⁰, Nd¹³², Xe¹²², and Zr¹⁰⁰ respectively

Click on image to enlarge

Figure (10-15): Shows the relation for Pu²⁴⁴, Yb¹⁶⁸, Gd¹⁵⁴, Er¹⁶², Dy¹⁶⁰, and Nd¹³² respectively

Click on image to enlarge

Acknowledgements

The author would like to express his thanks to Dr. Mohammad Abd Elsamea for his helpful to finish this work.

References

---

This work is licensed under a Creative Commons Attribution 4.0 International License.