Noise Minimization in Wireless Network

Gopal Singh¹ and H.N. Mishra²

¹Lalit Narayan Mithila University, Darbhanga - 846 008, India.
²Department of Physics, C.M.Sc. College, Darbhanga - 846 008, India.

DOI : http://dx.doi.org/10.13005/msri/090210

ABSTRACT:

The 2Dwhitenoise model has been extended to represent a modified power law that is realistic. It allows for finite moments for the interference.The white noise processes with a decaying power law.Impulse response functions are ideally suited for modeling the network self-interference in an ad hoc network.The nodes are distributed in a plane according to a Poisson point process. A stochastic impulse response function is used to model different random parameters like channel fluctuation, variable transmission power of the nodes etc. For a decaying power law, all the moments of the interference diverge.We have presented performance curves for the additive white Gaussian noise (AWGN) channel with and without variable transmission power at the nodes.We have imposed a guard zone around each receiver node in the network to modify the shot noise model to this channel access scheme and demonstrate the improvement in pernode throughput the guard zone.

KEYWORDS: Additive white Gaussian noise; White noise; Guard zone

Copy the following to cite this article: Singh G, Mishra H. N. Noise Minimization in Wireless Network. Mat.Sci.Res.India;9(2)

Copy the following to cite this URL: Singh G, Mishra H. N. Noise Minimization in Wireless Network. Mat.Sci.Res.India;9(2). Available from: http://www.materialsciencejournal.org/?p=1130

Introduction

We live in energy conscious era. In the community of electrical engineering energy consciousness has manifested itself in an increasing focus on low power circuits. Low power circuit implies low current or low voltage. They are more susceptible to the effect of noise. The fundamental physical concepts behind noise are simple. The myriad of random events that happen in microscopic scale cause fluctuation in the value of microscopic variables, such as voltage and currents and charge. Such variations are referred to as noise. The noise is called white noise if its power spectrum is flat. If its power spectrum is inversely proportional with frequency then it is called Pink noise or flicker noise. The most commonly adopted path loss model in literature is that the signal strength falls off as a decaying power law of the distance of transmission. For this model, when the nodes are distributed in R2 according to a Poisson point process (PPP), the exact distribution of the interference is analytically tractable only for a path loss exponent for the AWGN1 and Rayleigh fading channels2. For practical channels, therefore, it is of great interest to determine under what conditions the interference power converges to a Gaussian in distribution. The moments of the interference are excellent indicators in this regard4. However, when there is no power control, interferers close to a receiver contribute a lot more interference power than those further away, thus, violating the conditions for the central limit theorem5. Further, interferers arbitrarily close to a receiver can cause infinite interference in the decaying power law model and these causes all the moments of the interference to diverge. We eliminate diverging moments by using a modified power law to model the path loss so that it becomes physically meaningful for arbitrarily small distances as well. We derive the moment generating function of the interference for this modified power law by modeling the interference to be 2D Poisson shot noise process with a stochastic impulse response function. We havederived the additive white Gaussian noise (AWGN) as well as the Rayleigh fading channel for a wide range of path loss exponents. We also present performance results when the nodes employ variable transmission powers with nearest neighbor transmission. The results show that the modified path loss model does not differ by much from the original decaying power law model in terms of outage performance.The modified power law, interferers close to the receiver can easily swamp the desired signal, thus, resulting in low per-node throughputs. A solution to this problem is to modify the channel access scheme such that there is a guard zone around every receiver in which no interferers can be present. This results in significant improvements in the system performance even for small values of the guard zone6,7. We extend our shot noise model to such a channel access scheme and present performance curves for this model as well.

White noise background

Whitenoise results whena memory less linear filter is excited by a train of impulses derived from a homogeneous PPP with arrival rate μ [8]. The impulse response of the filter, f (t), can assume different shapeslike a triangle, rectangle, decaying exponential, decaying power law etc. More generally, the impulse shapes can be stochastic and may be randomly chosen from a family of shapes, f (k, t), with a random variable k. Here we have considered the stochastic impulse response model since specialization to the deterministic case is trivial.

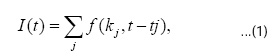
The shot noise (1) amplitude is given by equation (1). The arrival times {tj } are Poisson with rate μ and {kj } are iid random variables drawn from a common distribution and independent of {tj }. We have analyzed both the decayingpower law path loss model as well as a modified version that has advantage of having finite interference moments. Further, we have used the theory of equivalent shot noise processes to capture the stochastic nature of the transmission channel, variable transmission powers etc. We have also adapted this shot noise model to include a guard zone around every receiver and presented exact values as well as bounds on the throughput and outage probabilities that demonstrate the utility of the guard zone in improving the performance of an ad hoc network.

Modified power law

The decaying power law model is a good way to model path loss when the transmitter or interferer is far away from the receiver, but the model becomes physically meaningless for very small distances since the receiver can never receivemore than the transmitted power. To avoid this scenario, some authors adopt a path loss model of the form (1 + r) “ç. equivalently, we use the following modified power.

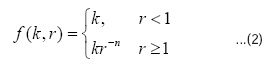
Law decay

The advantage of using this model is that it eliminates the singularity at r = 0 present in the original power law and provides a finite mean and variance for the total interference. This can be seen by modeling the total interference caused by all the transmitters at the origin to be the sum of 2 terms I1 and I2, where I1 is the total interference caused by all transmitters within a distance of 1 from the origin and I2is the total interference power due to all transmitters at distances greater than 1. Since the nodes are distributed according to a PPP, T1and T2are independent.

For two dimensional decaying power law shot noise process, the characteristic function is given by [3]

 

Guard zone in ad hoc networks

Often, the interferers that are really close to the origin are strong enough to completely swamp the desired signal. This leads to undesirably high outage probabilities. One way to overcome this problem is to modify the channel access scheme by imposing a guard zone of radius d0 around every receiver node. In other words, every receiver has an exclusion zone of radius d0 around it within which no interferers are allowed to transmit. this results in an improved outage and throughput performance. In this paper, we will only consider d0 ≥ 1 so that the path loss model is always given by the power law kr-η.

Results

The first set compares the per-node throughputs for 3 different transmission models when there is no guard zone in place. The second set of curves illustrates the usefulness of the guard zone in considerably improving the per-node throughput in an ad hoc network. The third set explores the impact that the modified power law has on the per-node throughput.We choose the system parameters to be λ = 1, Θ = 8 dB and η = 4 for all these curves. Fig. 1(a) shows that when all nodes transmit at the same power level, fading degrades the system performance and the maximum value of the per-node throughput, æ max, decreases by about 20%. . Fig. 1(a) also
presents æ values when nodes draw their powers.

Figure 1: (a) Per-node throughput for d0 = 0 (b) Per-node throughputs for the fading channel for d0 = 0 and d0 = 1 together with 2 upper bounds for the d0 = 1 case (c) Comparing the per-node throughputs for the decaying power law and the modified power law for the same set of system parameters

Click on image to enlarge

 

randomly. Similar to the fading channel, this model also degrades æmax by about 30% but the throughput curve has a very heavy tail. This means thatthe channel access scheme can be designed for a higher value of α without affecting the pernode throughput by much. Fig. 1(b) presents ζ values for the fading channel with and without a guard zone. All nodes transmit at the samepower level and we choose a guard zone of d0 = 1. The guard zone improves ζmax by almost 35% while simultaneously increasing the transmit probability that attains thisthroughput. However, the effect this has on increasing the sum throughput in the network is not immediately obvious, since the guard zone also reduces the effective number of nodes from which we can choose the set of transmitters. Fig. 1(c) shows that the throughput curves for the decaying and modified powerlaws are essentially the same and that we can use the compact outage expressions of the former with reasonable accuracy for the latter model also rather than use numerical integration or bounds for the incomplete Gamma function.

Conclusion

we have demonstrated the utility of the2D shot noise process to model the self-interference and perform outage and throughput analyses in a large wireless ad hoc network, where the nodes are distributed in R 2where L{f (k,r·) > x} represents the Lebesgue measure of the set with values greater than x. When f (k, t) = kt-η , 0 ≤ t < ∞, Ek [L{t : f (k, t) > x}] = Ek k1/η x-1/η . Thus, the ensemble of stochastic impulse responses kt-η is equivalent to the deterministic impulse response k0t-η for all η.
However,according to a PPP. We have analyzed both the decayingpower law path loss model as well as a modified version that has advantage of having finite interference moments. Further, we have used the theory of equivalent shot noise processes to capture the stochastic nature of the transmission channel, variable transmission powers etc. We have also adapted this shot noise model to include a guard zone around every receiver and presented exact values as well as bounds on the throughput and outage probabilities that demonstrate the utility of the guard zone in improving the performance of an ad hoc network.

References

1. G.P atounakis, Y.W .Li, and K.Shepard, A fully integrated on-chipDC–DC conversion and power management system. IEEE J. Solid- State Circuits 39: 443 (2004).
   CrossRef
2. R.J.Millik en, J.Silv a-Martínez, and E.Sánchez-Sinencio, Full onchipCMOS lowdropout voltage regulator. IEEE Trans. on Circuitsand Systems 54: 1879 (2007).
3. S.Y uan and B.C.Kim, Low dropout voltage regulator for wirelessapplications. 33rd Annual Power Electronics Specialists Conference, 2: pp.421–424 (2002).
4. V.Gupta, G.Rincon-Mora, and P.Raha, Analysis and design ofmonolithic, high PSR, linear regulators for SoC applications. Proc.IEEE Int. Syst. ChipConf ., Santa Clara, CA, pp.311–315 (2004).
5. V.Mannama, R.Sabolotn y, and V.Strik, “Ultra low noise low powerLDO design. Baltic Electronics Conference, pp.1–4 (2006).
6. G.Rincon-Mora and P.Allen, A low-voltage, low quiescent current,low drop-out regulator. IEEE J. Solid-State Circuits 33: 36 (1998).
   CrossRef
7. E. S. Sousa and J. A. Silvester, “Optimum Transmission Ranges in a Direct-Sequence Spread Spectrum Multihop Packet Radio Network”, IEEE J. Select. Areas Commun., vol.8, no. 4, 762-771, June 1990.
   CrossRef
8. M. Souryal, B. Vojcic and R. Pickholtz, “Ad hoc, Multihop CDMA Networks with Route Diversity in a Rayleigh Fading Channel”, Proc. IEEE MILCOM, vol. 2, Oct. 2001, pp. 1003-1007.
   CrossRef
9. F. Baccelli, B. Blaszczyszyn and P. Muhlethaler, “A Spatial Reuse ALHOA MAC Protocol for Multihop Wireless Mobile Networks”, Tech. Rep. 4955, Institut National de Recherche en Informatique et en Automatique (INRIA), Rocquencourt, Le ChesnayCedex, France, (2003).
10. J. Venkataraman and M. Haenggi, “Optimizing the Through- put in Random Wireless Ad Hoc Networks”, Allerton, 2004.
11. M. Haenggi, “ Link Modeling with Joint Fading and Dis-tance Uncertainty”, WiOpt ’06, Boston, MA, Apr. 2006.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.