Evolution of Order in Soft Materials under Nanoscale Confinement: Structure and Bonding
Introduction
Soft Matter
There are two classes of matter – hard and soft. Hard matter is characterized by shape rigidity and elasticity under small forces and plasticity and fragility above a certain magnitude of force, ability to sustain shear, and strong anisotropy in properties. In contrast, soft matter change their shape under very small forces, even thermal fluctuations, are unable to sustain shear and flow under stress, and have some viscous response. They have lower degree of anisotropy and constant free energy surfaces.
The microscopic or molecular forces in soft matter are mostly Hydrogen bonding forces, which may change from intra-molecular to intermolecular with passage to the condensed phases, the weak long range forces (Keesom forces) that arise due to dipoles and other higher order multipoles, the weak medium range forces such as London forces that arise due to induced dipoles, and of course the ubiquitous steric (electron-electron) and hydrophobic repulsion forces at short range.
Soft matter is characterized by shallow free energy minima, so that they can easily be taken to a non-equilibrium condition. They have weak inter-molecular forces and large internal entropy coming in most cases from the large amplitude intra-molecular motions. In other words, the molecular potential energy is comparable in magnitude to the internal kinetic energy of the molecule. The microscopic consequences of these energetics or bonding mechanisms are the passage to continuous symmetry from discrete symmetry and the passage to short-range order or correlation from long-range order or correlation.
Confinement: General Effects of Soft Matter
Confinement is apparently a simple and straightforward concept. Any system is said to be confined when its spatial extent is defined within a range of values. The system maybe a particle, either classical or quantum, either a real particle or a quasi-particle, a multi-particle body such as an atom or a molecule, a quasi-continuous bulk such as a solid, liquid or gas, a wave or a field. Confinement can be brought about by the use of an external force, such as by using electrical, magnetic, optical or thermal barriers, or by erecting rigid, material barriers. We shall call such confinement external or artificial confinement.
Confinement can also be caused by internal forces acting among the constituents of a system: the strong forces confine nucleons within the nucleus, electromagnetic forces confine electrons and nuclei within the atoms, atoms within molecules and condense gases into liquids and liquids into solids. This type of confinement can be designated as internal or natural confinement.
A major task of physical sciences has been, and still is, understanding this natural confinement and the hierarchy of structures and dynamics caused by it starting from elementary particles all the way to condensed matter and complex matter including living systems. In comparison, the study of artificially confined systems has been remark-ably sparse till recently. Though boundary conditions were ever present in studying any physical problem, their major effects were assumed to be at the boundaries only. Since any system studied was very large compared to the boundary region, this large size set the boundaries at separations big enough to kill any boundary effect within the sample. Again, the boundary conditions themselves were essentially put by hand, especially in the case of rigid material barriers, and this could not really be analyzed any further.
With the advent of micro- and nanotechnology pressure for device size reduction has now led to sample dimensions, such as the film thickness becoming smaller than molecular dimensions. At these levels of artificial confinement (nanoconfinement) such films show characteristics strikingly different from the properties these materials exhibit in the bulk, with crucial implications for most techno-logical applications based on such films. It has been shown that in confined systems van der Waals (vdW) interactions become longer in range, are no longer strictly pair wise additive, and depend on the dimensionality of the system. This scaling laws work on multilayered graphene and lead to a decreasing binding energy for an adsorbed molecule on graphene as a function of the number of graphene layers. This variation in van der Waals interactions could be exploited to control self-assembly in nanostructured materials [1].
Structural Studies of Confined Liquids
Basics of X-ray Scattering
The most striking difference of X-rays from other e. m. radiations that we encounter is that for them the refractive index of all materials is given by 1-d , where d (~ 10-5) is proportional to l2 and r, the former being the wavelength of X-rays and the latter being the total electron density of the material. The small values of d is consistent with the fact that X-rays pass through materials suffering very small deviations. However, the important point note is that as the density increases the material becomes ‘rarer’, i.e. gold is rarer than water to X-rays and all matter is rarer than vacuum!
As a consequence of the above property, for incident angle a at a flat sharp interface, if a is less than a certain critical angle ac the incident X-ray cannot penetrate the material but is totally reflected from it. This phenomenon is called total external reflection. For measurements of specular and off-specular components of this reflectivity of materials, the scattered X-ray intensity is collected using a detector as a function of the scattering vector q (2k = kfinal – kinitial) keeping one of the components of this vector, say qy = 0. The incident X-ray beam strikes at a grazing angle a and the scattered intensity is recorded in the plane of incidence at an angleb. In this geometry, the other two components of q become qz = (2π/l) (sinb + sina) and qx = (2π/l) (cosb – cosa). For specular reflectivity measurements, a = b = q, so that qx = 0 and qz = (4π/l)(sinq), and the scattering vector q is perpendicular to the surface. This provides information about the mean electron density as a function of depth (z). This is known as the electron density profile (EDP) [2].
X-ray Scattering Studies on Simple Liquids
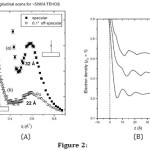
The structural effect of nanoconfinement was first seen directly in films of a simple liquid composed of nearly spherical, nonpolar molecules, tetrakis(2-ethylhexoxy)silane, or TEHOS, from x-ray reflectivity [3]. It was found from fitting the reflectivity data (Figure 1(a)) that there are three molecular layers near the solid-liquid interface (Figure 1(c)) and the Patterson function of the reflectivity also shows the peaks corresponding to total thickness (large peak) and the periods of the layers (Figure 1(b)).
Figure 1: (a) X-ray reflectivity data from TEHOS film in open circles, the best fit with a uniform-electron density model (dashed line) and the best fit electron density model with three layers (solid line). (b) Patterson functions, up-shifted for clarity, from the reflectivity profile (bold solid line, top), from the variable-density fit (thin solid line, middle) and from the uniform-density fit (dashed line, bottom). (c) Electron densities from the uniform-density model (dashed line) and the variable-density model (solid line). From ref 3.
Again, for even thick (5000Å) liquid films on silicon substrates, diffraction and specular reflectivity showed (Figure 2(A)) that the molecules form 3 to 6 layers at the solid-liquid interface (Figure 2(B)).
Figure 2: (A) X-ray scattering from ~ 5000Å thick liquid film of TEHOS on a clean, smooth Si substrate. In (a) the scattering vector q is normal to the substrate surface and in (b) it makes an angle of 0.1° to normal. Weak peak for scattering along the tilt is due to isotropic correlations present in bulk liquid. Strong, sharper peak along the normal direction is from the layers formed parallel to the silicon surface. (B) Electron density profiles obtained from fits to scattering data, (a) from fitting with one set of slabs (b) from fitting with a second set of slabs; and (c) from a fit with a decaying sine function density oscillation at the interface. Curves have been up-shifted for clarity. From ref 4.
It was found that thinning the film does not increase the effect, meaning that the layers are present even in a bulk liquid. For both thin and thick films, the layering amplitude goes down quickly as the substrate surface becomes rough. The liquids studied are non-conducting, non-polar, and non-reactive. Also the substrate surface has no lateral structure. Hence these observations hold true the interface between any simple liquid and smooth, hard solid [4].
X-ray Scattering Studies on Polymers
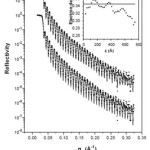
The first instance of spontaneous layering under nanoconfinement was seen through x-ray reflectivity in polystyrene films [5]. The oscillations in electron density have a periodicity Rg where Rg is the average radius of unperturbed gyration spheres of polystyrene in a dilute solution (Figure 3). In the following years, the huge body of research that has been carried out on artificially nanoconfined soft matter has had a sizable contribution from polymers in general and from polystyrene in particular and of these, again, a large number was done using synchrotron x-rays.
Figure 3: X-ray reflectivity profile of polystyrene film is shown in filled circles. The same profile is up-shifted to clarify the two model fits (line). The lower calculated profile uses a uniform thin film model (electron density profile (EDP) given by line inset) while the upper calculated profile uses the EDP shown by filled circles inset. From ref. 5.
A number of measurements on nanoconfined polymer by diverse research groups have shown anomalous density changes after the polymers are annealed below the bulk glass transition temperature (Tg). These changes are reversible as well as irreversible [6, 7, 4, 8-14]. These films also show unexpected instabilities [6, 15-17], and ageing behaviour [18-20] and surface diffusion [21] very different from bulk polymers. The glass transition temperature [22-32] becomes dependent on film thickness. There is a lower number of chain conformations in confined polymers [33] and the relaxation processes also get modified [19, 34].
These results have led to an intensive search for a general understanding of the physics of the confinement process. This is not available yet because the relative importance of Rg, which can be taken as the size of the polymer molecule in the maximum entropic state, and the film thickness R has not been established. In contrast to simple liquid films, polymer films often exhibit much stronger deviations from bulk behaviour. One probable reason is that, in contrast to small molecules, the polymer chains can adopt a huge number of different conformations. Hence an important factor may be the polymer molecular weight which, besides deciding Rg, decides the configurational entropy. Inelastic neutron scattering shows that the polymer chains are more constrained in films than in the bulk but also that this constraint does not change with molecular weight [35].
At present we do not have a detailed understanding of how this huge number of chain conformations are changed as the polymer is confined and how their mechanical and thermal properties are affected. A particularly important region is close to the glass transition temperature. A ‘confinement force’ (= kBT/R) can be defined, where kB, T, and R are the Boltzmann constant, absolute temperature, and the effective confinement dimension (e.g. film thickness), respectively. A competition between confinement and hydrodynamic forces on has to be invoked in this regard. This can explain, for example, the flow of polymer chains through a cylindrical pore with a diameter much smaller than its size, independently of chain topology [36].
For charged polymers under confinement, periodicity is given by the Kuhn length. Stable films of DNA molecules spin-coated from aqueous solution of DNA on amorphous quartz substrates are shown to exhibit layering of the molecules in three stacks parallel to the substrate. When the film is prepared from counterion added solution the layering is absent. These films have smaller thickness and enhanced surface roughness, although films under both conditions have liquid-like height-height correlations. These results are given by a model of film of a liquid of rod-like molecules where the counterion concentration in the liquid determines the rod (Kuhn) length [39].
Similar considerations are valid also for uncharged molecules with rod-like shapes. X-ray reflectivity studies on the interface of liquid squalane and Si substrates show that there are molecular layers near the interface, with the squalane molecular long axes parallel to the substrate. The results are consistent with those from molecular dynamics simulations and force measurements [40].
Bonding in Nanoconfined Fluids – X-ray Spectroscopy
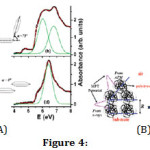
Synchrotron spectroscopic studies of bonding in nanoconfined polymers can throw some light on the confinement force or potential. Ultraviolet spectroscopy in the vacuum ultraviolet (VUV) region was carried out on atactic polystyrene (aPS) films with different film thickness R. This polymer is known to have physically coupled dimers of adjacent benzene rings pendant from the chain. These rings can be arranged in a V-shaped (oblique) or a shifted parallel (head-to-tail) configuration. As R is reduced below 4Rg VUV spectra reveal a change from the oblique to the head-to-tail configuration (Figure 4(A)). Simultaneously, as before, there is a spontaneous layering of the molecules of aPS in form of the gyration spheres as measured from X-ray reflectivity. However, it is clear from atomic force microscopy that there is also a reduction in cohesion that follows a (Rg/R)b dependence with b » 3. The reduction of in-plane (from microscopy) and out-of-plane (from reflectivity) cohesive energy in the films is explained by a repulsive, modified Pöschl-Teller intermolecular potential, with its strength decreasing with increase in R (Figure 4(B)). This reduction of cohesion can be explained by the reduction of the dimer dipole moment in the head-to-tail configuration of the benzene rings [37].
Figure 4: (A) Absorbance vs photon energy (in electronvolts) in the vacuum ultraviolet (vuv) range for atactic polystyrene films spin-coated on fused quartz. Film thicknesses R = 147.0 nm (a), 84.0 nm (b), 50.0 nm (c), and 40.0 nm (d) with data in circles, convolution of Gaussian fits in red and individual Gaussian fits in green lines, respectively. Assigned transitions are presented besides the spectral bands in oblique (a) and head-to-tail (c) configurations (shown inset as extracted from analysis of 1A1g → 1E1u) with a = dimer dihedral angle. (B) Cartoon of the confined polymer, showing the modified Pöschl-Teller-like intermolecular potential, as obtained from X-ray reflectivity and Atomic Force Microscopy. From ref. 37.
For R £ Rg, the benzene rings are also found to be aligned on a macroscopic scale causing a dependence of the electronic transition in the rings on the polarization of incident electromagnetic field. This ordering is confirmed from similar field polarization dependence in the X-ray Absorption Near Edge Structure (XANES) spectra of core electron (1s) transition, showing that the rings are oriented out-of-plane at 63° with the sample plane. Thus atactic polystyrene, which is inherently disordered in the bulk, transforms to an orientationally ordered phase under a certain degree of confinement [39].
Changes in Electrical and Thermal Properties
The spontaneous emergence of one-dimensional order due to confinement has had wide ranging consequences on soft materials. Here we would give two examples from the effects on electron and thermal transport of this ordering in soft materials.
Spin-coated films of atactic polystyrene of two different molecular weights have been studied with UV spectroscopy and X-ray reflectivity, the film thickness varying from ~2Rg to ~12Rg where Rg is the unperturbed radius of gyration of the polymer, which gave clear indication of excitonic interaction along the film thickness, and the mass of the effective exciton could also be measured. As the thickness is reduced below 4 Rg there is simultaneous emergence of one-dimensional order along the film thickness and localization of the exciton within the layers, with the effective mass becoming very large. Above this thickness, with the disappearance of the order, the exciton also becomes delocalized [41]. This is consistent with the decoupling of the adjacent benzene rings discussed in the previous section [37].
Nanofluids are a new class of fluids for heat transfer. They consist of fluids bearing nanoparticles and are of high technological value as their heat conductivities are much higher than normal fluids used for heat transfer. Thermal conductivity of nanofluids can only be explained by the invocation of a molecular layer at the nanoparticle-fluid interface, which acts as a bridge for thermal transport between nanoparticle and base fluid. This forms the key to the enhanced heat transfer properties of nanofluids [42]. The application of nanofluids as coolants has revolutionized the design of automobile radiator systems [43].
Some Other Confined Systems
In spite of the extensive research that has been and is being carried out on nanoconfined soft materials, it is evident, even from the glimpses provided here, that we are just at the beginning of this rich and productive branch of soft materials science. For example, even some of the basic questions concerning stability and dynamics of such well known spontaneously confined materials like Langmuir monolayers have not been addressed and, as a consequence, these nanoconfined systems are providing us with challenging new phenomena after a century of their discovery. In particular, the spontaneous formation of membranes at the water surface and the formation of two-dimensional mixtures of metal ions aided by these monolayers hold great promise. In connection with the former, the major question concerns the competition between the forces of in-plane clustering and out-of-plane diffusion, whose understanding and subsequent control can not only lead to tuneable two-dimensional and three-dimensional structures but to the unravelling of important biological mechanisms of drug-membrane lipid [44] interactions and DNA self-organization [45] under interfacial confinement. A related area, perhaps more fascinating in its physics content, which has received surprisingly scant attention is that of two-dimensional mixtures. The phases and stability of such mixtures, and also the formation of two-dimensional patterns through de-mixing [46], are expected to open new lines of research encompassing both soft condensed matter physics and physics at low dimensions, and this research is going to rely heavily on surface scattering techniques, both elastic and inelastic, provided by the bright beams of the synchrotron sources.
Conclusion
We present here a very brief review of soft materials like simple and complex fluids under confinement in films and at solid-fluid interfaces. It is clear that such confinement leads to a spontaneous one-dimensional structural ordering normal to the direction of confinement. The periodicity developed is a characteristic microscopic length – the molecular size for simple liquids, the gyration diameter for neutral polymers, and the Kuhn length for charged macromolecules. For the polymer, a molecular reorganization co-evolving with the ordering could be observed as also the emergence of an intermolecular repulsion. It was also seen that this ordering strongly affects the exciton transfer in films and thermal transfer at the solid-fluid interfaces of nanofluids.
Acknowledgement
The author acknowledges the Department of Atomic Energy for funding a Raja Ramanna Fellowship and the Director, CSIR-Central Glass and Ceramic Research Institute for hosting an Emeritus Scientist position.
Funding Source
This research received no specific grant from any funding agency.
Conflict of Interest
The authors have no conflicts of interest to disclose.
References
- Vivekanand V. Gobre and Alexandre Tkatchenko, Nat. Comm. DOI: 10.1038/ncomms3341 (2013).
CrossRef
- M.K. Sanyal, A. Datta, and S. Hazra, Pure Appl. Chem. 74, 1553 (2002).
CrossRef
- C.-J. Yu, A. G. Richter, A. Datta, M. K. Durbin, and P. Dutta, Phys Rev Lett 82, 2326 (1999).
CrossRef
- C.-J. Yu, A. G. Richter, J. Kmetko, S.W. Dugan, A. Datta, and P. Dutta, Phys Rev E 63, 021205 (2001).
CrossRef
- M. K. Sanyal, J. K. Basu, A. Datta and S. Banerjee, Europhys. Lett. 36, 265 (1996).
CrossRef
- Vladimir M. Kaganer, Helmuth Mohwald, and P. Dutta, Rev. Mod. Phys. 71, 779 (1999).
CrossRef
- G. Reiter, Europhys Lett, 23, 579 (1993).
CrossRef
- W. J. Orts, J. H. van Zanten, W. L. Wu, S. K. Satija, Phys Rev Lett 71, 867 (1993).
CrossRef
- G. Reiter, P.-G. de Gennes, Eur Phys J E 6, 25 (2001).
CrossRef
- M. Mukherjee, M. Bhattacharya, M. K. Sanyal, T. Geue, J. Grenzer, U. Pietsch, Phys Rev E 66, 061801-1 (2002).
CrossRef
- M. Bhattacharya, M. K. Sanyal, T. Geue, U. Pietsch, Phys Rev E, 71, 041801-1 (2005).
CrossRef
- T. Kanaya, T. Miyazaki, H. Watanabe, K. Nishida, H. Yamana, S. Tasaki, D. B. Bucknall, Polymer 44, 3769 (2003).
CrossRef
- T. Miyazaki, K. Nishida, T. Kanaya, Phys Rev E 69, 022801-1 (2004).
CrossRef
- H. Richardson, I. Lopez-Garcia, M. Sferrazza, J. L. Keddie, Phys Rev E 70, 051805-1 (2004).
CrossRef
- C. Bollinne, S. Cuenot, B. Nysten,A. M. Jonas, Eur Phys J E 12, 389 (2003).
CrossRef
- O. K. C. Tsui, C. Russel, Polymer Thin Films (World Scienti c, Sin-gapore, 2008).
CrossRef
- O. K. C. Tsui, Y. J. Wang, F. K. Lee, C. H. Lam, Z. Yang, Macro-molecules 41, 1465 (2008).
CrossRef
- R. D. Priestley, L. J. Broadbelt, J. M. Torkelson, Macromolecules 38, 654 (2005).
CrossRef
- G. Reiter, M. Hamieh, P. Damman, S. Sclavons, S. Gabriele, T. Vilmin, E. Raphael, Nat Mater 4, 754 (2005).
CrossRef
- S. Kawana and R. A. L. Jones, Eur Phys J E, 10, 223 (2003).
CrossRef
- Z. Fakhraai, J. A. Forrest, Science 319, 600 (2008).
CrossRef
- J. L. Keddie, R. A. L. Jones, R. A. Cory, Europhys Lett 27, 59 (1994).
CrossRef
- J. A. Forrest, K. Dalnoki-Veress, J. R. Stevens, J. R. Dutcher, Phys Rev Lett 77, 2002 (1996).
CrossRef
- E. Dalnoki-Veress, J. A. Forrest, C. Murray, C. Gigault, J. R. Dutcher, Phys Rev E, 63, 031801-1 (2001).
CrossRef
- M. Alcoutlabi, G. B. McKenna, J Phys Condens Matter 17, R461 (2005).
CrossRef
- R. D. Priestley, C. J. Ellison, L. J. Broadbelt, J. M. Torkelson, Science 309, 456 (2005).
CrossRef
- S. Peter, H. Meyer, J. Baschnagel, J Polym Sci Part B-Polym Phys 44, 2951 (2006).
CrossRef
- A. Serghei and F. Kremer, Macromol Chem Phys 209, 810 (2008).
CrossRef
- S. Kim, S. A. Hewlett, C. B. Roth, J. M. Torkelson, Eur Phys J E 30, 83 (2009).
CrossRef
- S. Peter, S. Napolitano, H. Meyer, M. Wubbenhorst, J. Baschnagel, Macromolecules 41, 7729 (2008).
CrossRef
- C. Rotella, S. Napolitano, M. Wuebbenhorst, Macromolecules 42, 1415 (2009).
CrossRef
- S. Napolitano, A. Pilleri, P. Rolla, M. Wubbenhorst, ACS Nano 4, 841 (2010).
CrossRef
- L. Si, M. V. Massa, K. Dalnoki-Veress, H. R. Brown, R. A. L. Jones, Phys Rev Lett 94, 127801-1 (2005).
CrossRef
- P. Damman, S. Gabriele, S. Coppee, S. Desprez, D. Villers, T. Vilmin, E. Raphael, M. Hamieh, S. Al Akhrass, G. Reiter, Phys Rev Lett 99, 036101-1 (2007).
CrossRef
- Rintaro Inoue, Toshiji Kanaya, Koji Nishida, Itaru Tsukushi, and Kaoru Shibata, Phys. Rev E 77, 032801 (2008).
CrossRef
- Chi Wu and Lianwei Li, Polymer 54, 1463 (2013).
CrossRef
- Sudeshna Chattopadhyay, Alokmay Datta, A. Giglia, N. Mahne, A. Das, and S. Nannarone, Macromolecules 40, 9190 (2007).
CrossRef
- Sudeshna Chattopadhyay, A. Datta, A. Giglia, N. Mahne, S. Nannarone, arXiv preprint arXiv:0709.2528 (2007).
CrossRef
- Nupur Biswas, Sreeja Chakraborty, Alokmay Datta, Munna Sarkar, Mrinmay K. Mukhopadhyay, Mrinal K. Bera, and Hideki Seto, arXiv:1404.0782v1[cond-mat.soft].
CrossRef
- Haiding Mo, Guennadi Evmenenko, and Pulak Dutta, Chem Phys Lett 415, 106 (2005).
CrossRef
- Sudeshna Chattopadhyay and Alokmay Datta, Phys. Rev. B 72, 099539 (2005).
CrossRef
- Haifeng Jiang, Qianghui Xu, Chao Huang and Lin Shi, App. Phys. A 118, 197 (2015).
CrossRef
- Neeti Arora and Munish Gupta, Renewbl. Sustainbl. Energy Rev. 134, 110242 (2020).
CrossRef
- Sarathi Kundu, Hirak Chakraborty, Munna Sarkar, and Alokmay Datta, Coll. Surf. B: Biointerfaces 70, 157 (2009).
CrossRef
- Nupur Biswas, Masatoshi Ichikawa, Alokmay Datta, Yuko T. Sato, Miho Yanagisawa, and Kenichi Yoshikawa, Chem. Phys. Lett. 157, 539 (2012).
CrossRef
- Madhumita Choudhuri and Alokmay Datta, J. Nanosci. Nanotechnol. 14, 2901 (2014).
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.
 Material Science Research India An International Peer Reviewed Research Journal
Material Science Research India An International Peer Reviewed Research Journal