Martensitic Nanostructure in NiAl Alloys: Tip Splitting and Bending

Arunabha M. Roy* University of Michigan, Aerospace Engineering Department, Ann Arbor, MI 48109, U.S.A. Corresponding Author Email: arunabhr@umich.edu

DOI : http://dx.doi.org/10.13005/msri.17.special-issue1.02

ABSTRACT: A phase-field (PF) model for the phase transformation (PT) between austenite and martensite and twinning between two martensite is presented where PT is described by a single order parameter. Such a description helps us to obtain the analytical solution of interface energetics and kinetics. PF-elasticity problems are solved for cubic-to-tetragonal PT in NiAl. The stress and temperature-induced PT and corresponding twinning and growth of the martensitic phase inside a nanocrystal are simulated. It reproduces nontrivial experimentally observed nanostructure such as splitting and bending of martensitic nanostructure as well as twins crossing. The evolution and morphology of such interesting nanostructures are discussed. KEYWORDS: Ginzburg-Landau (G-L) Equation; Phase-Field Approach; Phase Transition in Martensite

Copy the following to cite this article: Roy A. M. Evolution of Martensitic Nanostructure in NiAl Alloys: Tip Splitting and Bending. Mat. Sci. Res. India; Special Issue (2020).

Copy the following to cite this URL: Roy A. M. Evolution of Martensitic Nanostructure in NiAl Alloys: Tip Splitting and Bending. Mat. Sci. Res. India; Special Issue (2020). Available from: https://bit.ly/2P8yG2s

Short  Communication

Phase-field (PF) method is a powerful technique to simulate different types of PTs. One of the main applications of this method can be found in PT in solid phases such as martensitic PT.^1-8 Martensitic PT plays an important role for overall material response by altering nanostructure in such materials. Different shape memory alloys exhibit martensitic PTs and form different interesting and non-trivial nanostructure during PT due to stress and temperature.^9-14 For stress-induced martensitic PT, the material interface experiences biaxial tension of magnitude of the surface energy. However, it is difficult to characterize such interface as material parameters in general at the interface are unknown for heterogonous nature of the interface. Hence it is challenging to formulate and incorporate constitutive equations that can capture the strong heterogonous properties and complex stress-strain fields in the interface. This problem has been solved by formulating a constitutive equation which successfully introduces interfacial stress in the martensitic interface.^15-18 Such interface stress has also been introduced in multiphase PF theory for generalized n phases^19-21 as well as martensitic PTs.^15-18 The PF theory in,^11-14 formulated in polar coordinate system, requires single order parameter to capture martensite-martensite PT and twinning. Such a description allows us to get the analytical solution of interface profile, energy, and width as well as interfacial stress. This interfacial stress is thermodynamically consistent even for sharp interface limit. In general, martensite   possess sharp tips with  thickness of the order of 1nm. Hence, the interface stress plays a significant role for the evolution of different non-trivial nanostructures which were observed in the experiments.  In this work, the stress and temperature-induced PT and corresponding twinning and growth of the martensitic phase inside a nanocrystal are simulated with a proper implementation of interface tension in the interface. The combined A↔T and T₁ ↔T₂ PTs and corresponding microstructure evolution similar to experimentally observed microstructures of NiAl alloy^{22, 23} are discussed. The novelty of this work is that this model able to capture the nontrivial experimentally observed microstructures in our simulations both qualitatively and quantatively. It includes tip splitting and bending, and twins crossing.

In this model,^11-14 austenite A and two martensitic variants, T₁ and T₂ are considered. The radial order parameter Υ describes A↔T₁ and A↔T₂ PTs. The angular order parameter ϑ describes T₁↔T₂ (variant-variant) transformations. It is bounded by 0 ≤ ϑ ≤ 1 . The Cauchy stress tensor has the following form^11-14:

The stress tensor can be split into two part,

The dissipative part and the surface tension contribution are obtained by decomposing σ. The non-mechanical type of stress

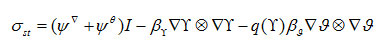
is called “surface tension”. It is localized at the interface.

In this work, an initial random distribution of austenite nuclei are considered in 50nm ×50nm sample and homogeneous biaxial strain is applied at the surfaces of the sample. For detail description, readers are suggested to look.^11-14 In the final microstructure, bending and splitting of martensitic tips are observed in Fig. 1-(c, e), similar to experiments^{21, 22} In Fig. 1-(c), martensitic variant T₂ is at an angle θ=76.9^o. Since, there is an invariant plane interface in-between T₁ and T_2, it requires mutual rotation of these variants by the angle β= 12.1^o. Here the angle between horizontal and vertical variants T₂ is 1.5b = 18.15^o .As shown in In Fig. 1, our simulation result is in good agreement with the experimental micrograph.^{21, 23}

Click on image to enlarge

Due to reduction in the interface energy at invariant plane interface, narrowing and bending of the tips of T₂ horizontal plates occurs. For intermediate stage of the evolution, one twin penetrates into  the region of another twin as shown in Fig. 1-(e). This results in crossed twins type microstructure.  Such microstructure was also observed in experiments.²² Moreover, most of the cases the twin planes are visibly bending or reorienting in areas close to the interface and the small microtwin variants penetrating into the other variants. In these zones, the formation of a needle like microtwin occurs which usually tapered to the microtwin boundary, and the penetrating microtwin variant tends to disappear.

Conclusion

Summarizing, a PF approach is applied to multivariant martensitic phase transformations and twinning within these variants. The stress and temperature-induced PT and corresponding twinning and growth of the martensitic phase inside a nanocrystal are simulated. It reproduces nontrivial experimentally observed nanostructure such as splitting and bending of martensitic nanostructure as well as twins crossing. The evolution and morphology of such interesting nanostructures are discussed. It is found that interfacial stress significantly influences the nanostructure evolution of martensitic PT in NiAl alloys.

Acknowledgement

The help of Dr. V.I. Levitas from Iowa State University is gratefully acknowledged.

Funding Source

Los Alamos National Lab (Contract No. 104321) and  National Science Foundation (Grant No. CMMI-0969143)

Conflict of Interest

There is no conflict of interest.

References

1. V. I. Levitas, D. L.  Preston, Three-dimensional  Landau  theory  for  multivariant  stress-induced  martensitic  phase  transformations.  I. Austenite ↔ martensite., Phys. Rev. B   66 (2002a) 134206.
2. V. I. Levitas, D. L. Preston, Three-dimensional Landau theory for multivariant stress-induced martensitic phase transformations. II. Multivariant phase transformations and stress space analysis., Phys. Rev. B   66 (2002b) 134207.
3. V.I. Levitas, D.L. Preston, D.W.  Lee, Three-dimensional  Landau  theory  for  multivariant  stress-induced  martensitic  phase  transformations  III. Alternative potentials, critical nuclei, kink solutions, and dislocation theory., Phys. Rev. B  68 (2003) 134201.
4. V. I.  Levitas, D. W.  Lee, D. L.  Preston, Interface propagation and microstructure evolution in phase field models of stress-induced martensitic phase transformations, Int. J. of Plas. 26 (2010) 395-422.
5. M. Javanbakht, M. Adaei, Formation of stress- and thermal-induced martensitic nanostructures in a single crystal with phase-dependent elastic properties., J. Mater. Sci. 55 (2019).
6. M. Javanbakht, M. Adaei, Investigating the effect of elastic anisotropy on martensitic phase transformations at the nanoscale, Comput. Mater. Sci. 167 (2019) 168-182.
7. M. Javanbakht, E. Barati, Martensitic phase transformations in shape memory alloy: phase field modeling with surface tension effect, Comput. Mater. Sci. 115 (2016) 137–144.
8. H. Babaei, A. Basak, V. I.  Levitas, Algorithmic aspects and finite element solutions for advanced phase field approach to martensitic phase transformation under large strains, Comput. Mech. 64 (2019) 1177-1197.
9. V. I.  Levitas, M. Javanbakht, Surface tension and energy in multivariant martensitic transformations: phase-field theory, simulations, and model of coherent interface., Phy. Rev. Lett. 105 (2010) 165701.
10. V. I.  Levitas, M. Javanbakht, Surface-induced phase transformations: multiple scale and mechanics effects and morphological transitions., Phy. Rev. Lett. 107 (2011) 175701.
11. V. I. Levitas, A. M.  Roy, D. L. Preston, Multiple twinning and variant-variant transformations in martensite: Phase-field approach., Phys. Rev.B  88 (2013) 054113.
12. A.M. Roy, Influence of  Interfacial Stress on  Microstructural Evolution in NiAl Alloys., JETP Lett. (2020) (in press). DOI: 10.1134/S0021364020150023. (https://doi.org/10.1134/S0021364020150023).
13. A.M. Roy,. Effects of interfacial stress in phase field approach for martensitic phase transformation in NiAl shape memory alloys., App. Phys. A  126 (2020)  576.
14. A.M. Roy, Influence of interfacial stress on microstructural evolution in NiAl alloys., Pis’ma v ZhETF (Письма в ЖЭТФ) 112(3-4) (2020) 187. DOI: 10.31857/S1234567820150070
15. V. I. Levitas, Interface stress for nonequilibrium microstructures in the phase field approach: Exact analytical result, Phys. Rev.B  87 (2013) 054112.
16. V. I. Levitas, Thermodynamically consistent phase field approach to phase transformations with interface stresses, Acta Mater.  61 (2013) 4305.
17. V. I. Levitas, Phase-field theory for martensitic phase transformations at large strains, Int. J. Plast. 49 (2013) 85.
18. V. I. Levitas, Phase field approach to martensitic phase transformations with large strains and interface stresses, J. Mech. Phys. Solids  70 (2014) 154.
19. V. I. Levitas, A. M. Roy, Multiple phase field theory for temperature- and stress-induced phase transformations, Phys. Rev. B 91 (2015) 174109.
20. V. I. Levitas, A. M. Roy, Multiphase phase field theory for temperature-induced phase transformations: Formulation and application to interfacial phases, Acta Mat. 105 (2016) 244-257.
21. A.M. Roy, Phase Field Approach for Multiphase Phase Transformations, Twinning, and Variant–Variant Transformations in Martensite, Graduate Thesis and Dissertations 14635, Iowa State University, Ames (2015).
22. Ph. Boullay, D. Schryvers, R. V. Kohn, Bending martensite needles in Ni65Al35 investigated by two-dimensional elasticity and high-resolution transmission electron microscopy, Phys. Rev. B 64 (2001) 144105
23. Ph. Boullay, D. Schryvers, J. M. Ball, Nano-structures at martensite macrotwin interfaces in Ni65 Al35. Acta Mat. 51 (2003) 1421-1436

---

This work is licensed under a Creative Commons Attribution 4.0 International License.