Determination of Young’s Modulus of Aluminium, Copper, Iron, Brass and Steel Alloys by Using Double Exposure Holographic Interferometry (DEHI) Technique

H. R. Kulkarni¹ , S. N. Shukla² and M. B. Dongare³

¹KJEI’s KJ College of Engineering and Management Research, Pune, Maharashtra, India

DOI : http://dx.doi.org/10.13005/msri/140207

ABSTRACT:

Double Exposure Holographic Interferometry (DEHI) technique has wide applications in the field of science and engineering. DEHI can be used to determine very small surface changes in an object at very small interval of time.

In present case, DEHI technique is used to record the hologram of the same object at different times subjected to different loads. This method has been advantageously used to determine Young’s Modulus (Y) of Aluminium, Copper, iron, brass and some steel alloys. It is found that the values of Y obtained by using DEHI technique are in close agreement with standard values of Y available for respective metals and their alloys. The method is also used to make standard relation between effect of carbon composition and Y of steel alloys.

KEYWORDS: DEHI; Double Exposure Holographic Interferometry; Young’s Modulus

Copy the following to cite this article: Kulkarni H. R, Shukla S. N, Dongare M. B. Determination of Young’s Modulus of Aluminium, Copper, Iron, Brass and Steel Alloys by Using Double Exposure Holographic Interferometry (DEHI) Technique. Mat.Sci.Res.India;14(2)

Copy the following to cite this URL: Kulkarni H. R, Shukla S. N, Dongare M. B. Determination of Young’s Modulus of Aluminium, Copper, Iron, Brass and Steel Alloys by Using Double Exposure Holographic Interferometry (DEHI) Technique. Mat.Sci.Res.India;14(2). Available from: http://www.materialsciencejournal.org/?p=6086

Introduction

DEHI technique is used to record the holograms of same objects at different times.¹ This method has some advantages over other techniques particularly for studying transient phenomenon. The analysis is, of course, not significantly different from analysis given for single exposure technique and the resulting interference pattern is determined by the phase difference between the object wave in first position and object wave in second position.² This technique can be used in the study of stress-strain relation, and fluid mechanics,³ fracture mechanics for non-destructive testing.⁴  Hologram interferometry can also be used to show changes of shape in a specimen.⁵

     The qualitative determination of mechanical strain[6] on surface of arbitrary shaped object through holographic interferometry requires the solution of following three basic problems.

1. Relation between surface strain and surface displacement;
2. Relation between derivation of the surface displacement and the interference fringes in the image plane;
3. Interpolation of interference fringe pattern and quantitative determination of interference phase.

The development of practical technique for obtaining quantitative information⁷ from double- exposure hologram is still one of the most interesting problems in holographic interferometry. The applications of holographic interferometry techniques to non-destructive testing have received a great deal of attention in recent years. Because of its extreme sensitivity, holographic interferometry allows for the detection of small defects and anomalies in diffuse three dimensional objects.^7-9 Various holographic methods are described^10-12 to measure 3-D displacements of object under loading. These include viewing of surface of object through different points of hologram through various angles and counting the number of fringes that pass through the point under consideration between the two exposures is very small or less than one fringe. The success of holographic non-destructive testing¹³ of a material, however, depends upon the stressing technique adopted. The stressing should deform the body under test in such a manner that the ‘good’ areas are distinguished from the ‘bad’ areas simply by studying the interference generated on the holographic interferogram.

Measurement of Young’s Modulus¹⁴

Youngs modulus of material can be calculated using deflection equation of cantilever. The deflection equation of cantilever is given by,

ΔZ = (WL³) / (3YI)                              …..(1)

Where,

W = load applied in kg

L = effective span in cm

Y = Young’s modulus in kgF / cm²

I = moment of inertia in cm⁴, can be obtained from physical dimensions of

cantilever. Its value for rectangular beam of width ‘a’ and thickness ‘b’  

is ab³ / 12.

Equation (1) can be written as ,

Y = (WL³) / (3 I ΔZ)……………………(2)

Where                       ΔZ is measured from holographic interferometry.

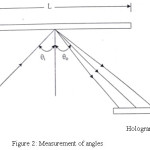
Let θ_i and θ_o be the  angle defining the directions of illumination and observation respectively. These are measured from the geometry of figure as shown in Figure 2. The path difference Δ between two rays scattered from the two identical points on the object is given by,

Δ = ΔZ. n. (Cos θ_i + Cos θ_o)………………………..(3)

Where,                               n = refractive index, usually 1 for air.

If there are N fringes produced up to the span length L of the cantilever counted from the fixed end, then,

ΔZ = Nλ /  (Cos θ_i + Cos θ_o) …………………(4).

Substituting the value of ΔZ in equation 2. Then the value of Young’s modulus can be calculated from,

Y =  WL³ (Cos θ_i + Cos θ_o) / (3 I Nλ)……………(5)

Experimental Results of Y for metals and alloys

Young’s modulus has been determined for aluminium, copper, iron, brass and certain steel alloys by using DEHI technique. The samples for this purpose were obtained from Mayura Steel Industries, Kolhapur. The constitution of alloy and their composition as well as their dimensions are given in Table 1.

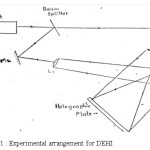
The experimental arrangement for recording double – exposure hologram with loaded objects is as shown in Figure 1.

Figure 1 : Experimental arrangement for DEHI

Click on image to enlarge

 

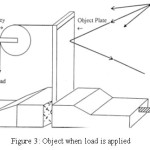
Double exposure holograms of the corresponding objects were recorded at two different situations. One at its normal state and other at deformed state due to application of load. For the application of load, string and pulley arrangement was used as shown in Figure 3.

Figure 2: Measurement of angles

Click on image to enlarge

 

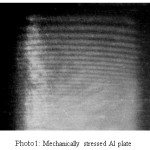
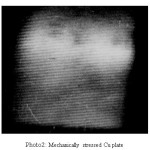
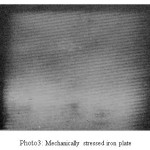
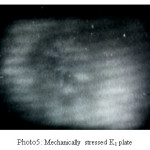
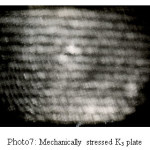
The holograms were recorded on 8E75HD holographic plate using He-Ne laser of 2mw. The two beam off axis method was used to record the holograms. The holograms were processed in usual manner. The reconstructed holograms revealed number of fringes located on the surface of metal plates. The exposure time of 7sec each was given to both the exposures. The object dimensions have been accurately measured and presented in Table 2. The number of fringes were accurately counted. These are shown in Photographs 1-7.  Making the use of Equation (5), Young’s modulus of material of object has been determined. The values of Y calculated by this method have been entered in Table 2 along with object dimensions and angle of illumination and scattering of light from the object surface.

Figure 3: Object when load is applied

Click on image to enlarge

 

Photo 1: Mechanically stressed Al plate

Click on image to enlarge

 

Photo 2: Mechanically stressed Cu plate

Click on image to enlarge

 

Photo 3: Mechanically stressed iron plate

Click on image to enlarge

 

Photo 4: Mechanically stressed brass plate

Click on image to enlarge

 

Photo 5: Mechanically stressed K₁ plate

Click on image to enlarge

 

Photo 6: Mechanically stressed K₂ plate

Click on image to enlarge

 

Photo 7: Mechanically stressed K₃ plate

Click on image to enlarge

 

Results and Discussion

With the help of DEHI technique, the calculated values of Y for Aluminium, Copper, brass, iron and steel alloys plates are given in Table 2. It is found that the values of Y calculated are in close agreement with the standard values.

In case of steel alloys K₁, K₂ and K₃ (general titles given) value of Y found is higher than that of iron. It is mostly dependent of percentage of carbon in that alloy. This percentage of carbon is given in Table 1.  The carbon content of K₁, K₂, and K₃ is in the increasing order resulting to increase in their Young’s modulus. For sample K₁, it is 1.04 times greater than that of iron and K₂ it is observed 1.08 times greater while for K₃ 1.19 time greater  that of iron. The values determined for samples K₁, K₂, and K₃ are not available anywhere. The values of Y determined for Aluminium, Copper, brass, and iron are in close agreement with the available standard values. These results indicate DEHI technique can be used to determine the standard values of Young’s modulus of elastic material. This result confirms that the values of Y determined for samples K₁, K₂, and K₃ are correct.

Table 1: Constituents of steel alloys

Constituents %	Steel samples
	K1	K2	K3
C	0.184	0.40	1.17
Mn	0.93	0.090	13.15
Si	0.41	0.42	0.42
S	0.037	0.039	0.004
P	0.030	0.038	0.066
Cr	0.099	0.763	0.23
Ni	—	3.258	0.038
Mo	30.00	0.231	—

 

Table 2: Determined values of Y

Object Plate	Length L in cm	Breadth ‘a’ in cm	Depth  ‘b’ in cm	Load applied W in kg	No of fringes located on the object	Angle of                       (in degrees)		Young’s Modulus      Y     in kgF / cm2
						Illumination   θi	Scattering   θo	Determined values	Standard Values
Al	3.00	3.00	0.110	0.007	10	6˚ 30’	46˚	0.672 x 106	0.70 x 106
Cu	1.80	3.00	0.110	0.650	11	6˚ 00’	44˚ 30’	1.240 x 106	1.240 x 106
Iron	3.00	3.00	0.120	0.140	36	5˚ 30’	48˚	2.130 x 106	2.00 x 106
Brass	3.00	3.00	.011	0.015	15	6˚ 30’	44˚ 30’	0.970 x 106	0.90 to 1    x 106
K1	2.40	3.00	0.380	3.00	12	4˚ 30’	48˚	2.230 x 106	——
K2	2.40	2.90	0.353	3.00	15	7˚ 00’	46˚	2.311 x 106	——
K3	2.50	3.00	0.310	1.800	13	4˚ 30’	48˚	2.549 x 106	——

 

References

1. Helfinger L. O., Brooks R. E and Wuerker R. F. J. Appl. Phys. 1966;37:642.
2. Tanner L. H.  J. Sci. Instrum. 1967;44:1015.
   CrossRef
3. Dudderar T. D. Exp. Mech. 1969;9:281.
   CrossRef
4.  Steel W. H. Interferometry, Cambridge University Press. 1968;188.
5. Dandliker R.,  Eliasson B.,  Ineichen B.,  Motterer F. M. The engineering use of Coherent Optics, Cambridge University Press, Cambridge. 1976;99-117.
6.  Marom E.,  Friesem A. A.,Avnear W. E. Applications of Holography and Optical data processing, Pergamon Press, London. 1977;225.
7. Robertson E. R. The Engineering Uses of Coherent Optics, Cambridge University Press. 1976.
8. Erf R. K.  Holographic Non-destructive Testing, Academic Press, New York. 1974.
9.  Hariharan P. Optical Holography, Principles, Techniques and Applications, Cambridge University Press. 214. 1984.
10. King III P. W.  Appl. Opt. 1974;13:231.
    CrossRef
11.  Hansche B. D., Murphy G. G. Appl. Opt. 1974;13:630.
    CrossRef
12.  Sarma A. V. S. S. S. R.,   Kutty G. T. G. Appl. Opt. 1978;17:3964.
    CrossRef
13. Mehta P. C., Mohan D.,Bhan C.,Lal P., Rhidaynath R.  Optics and Laser Technology. 1982;269.
    CrossRef
14.  Sirohi R. S. A Course of Experiments with He-Ne laser, Wiley Eastern Limited, New Delhi. 1986;67.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.