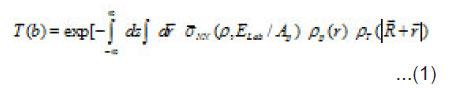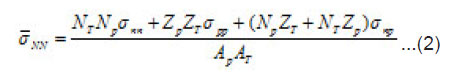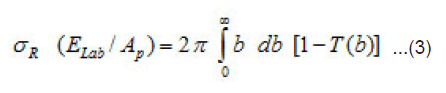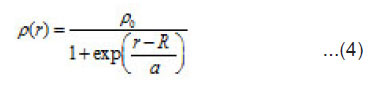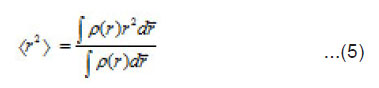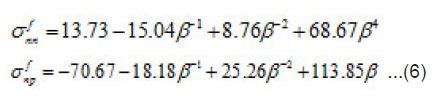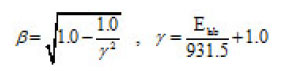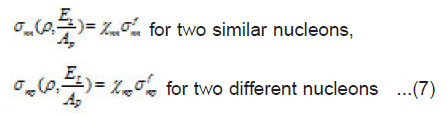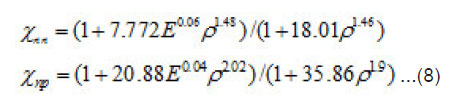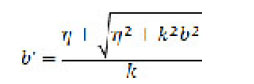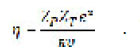The Behavior of Reaction Cross-Section at Low and Intermediate Energies by Considering in-Medium Effects in Snn for Light and Heavy Target Nuclei

H. El-Gebaly

Department of Physics, Faculty of Science, Cairo University, Giza, Egypt.

DOI : http://dx.doi.org/10.13005/msri/070117

ABSTRACT:

The in-medium effects in nucleon-nucleon cross-section were treated using different approaches. We study the variation of σ_R with different values of rms. Also we study the variation of sR with different values of incident energy per projectile nucleon for light interacting pair ¹²C-¹²C and heavy target nucleus pair¹²C-²⁰⁸Pb. The coulombs repulsion was taken into consideration by assuming a simple model. We found that the in-medium effects on σ_R are small when the target nucleus becomes heavy.

KEYWORDS: Nucleon-nucleon cross-section; Light and heavy target nuclei

Copy the following to cite this article: El-Gebaly H. The Behavior of Reaction Cross-Section at Low and Intermediate Energies by Considering in-Medium Effects in Snn for Light and Heavy Target Nuclei. Mat.Sci.Res.India;7(1)

Copy the following to cite this URL: El-Gebaly H. The Behavior of Reaction Cross-Section at Low and Intermediate Energies by Considering in-Medium Effects in Snn for Light and Heavy Target Nuclei. Mat.Sci.Res.India;7(1). Available from: http://www.materialsciencejournal.org/?p=2255

Introduction

In recent years the total reaction cross-section of heavy ions has become the focus of extensive theoretical^1-4 and experimental⁵ attention. The reaction cross-section also finds applications in diverse research areas such as radiobiology and space science.^6,7 Moreover the total reaction cross-section, σ_R, is one of the most important physical quantities describing the properties of nuclear reaction. The reaction cross-section is used to calculate the nuclear root mean square radius (rms) which is necessary to understand the nucleus-nucleus reactions and scattering mechanisms.¹ In Ref.⁶, the effective rms radii of nucleon distribution of B, Be and He isotopes had been deduced by comparing the experimental data for the reaction cross-section by theoretical calculations based on Glauber theory. The optical limit to Glauber theory is usually used with appreciable success to describe the reaction cross section between complex nuclei.^2,3,8 The inputs to these calculations are the nucleon- nucleon (NN) reaction cross-section, σ_NN, and the density distribution of the interacting nuclei. Recently, this method has been used to determine the rms radii of the interacting nuclei and to study halo nuclei.^3,6,8,9 The value of σ_R for a pair of interacting nuclei calculated in the frame work of the optical limit of Glauber theory is affected by different factors. One of these factors is the method of treating in-medium effects. Also, it is sensitive to the range of the NN force and the values of rms radii of the nuclei considered. σ_R is usually calculated by assuming the zero-rang force [3] of the interacting nucleons and the NN reaction cross-section is considered through different approaches [ 1,5,9]. First, σ_NN is taken directly as free NN cross-section, σ^f_NN [8], without density dependence or evaluated at constant density usually assumed to be equal to saturation nuclear matter density ( ρ=0.17 fm^-3 )[1,9].This approach in treating in-medium effects permits extracting σ_NN out of integrations since, in this case, it has constant value. Moreover for constant value of σ_NN and assuming Gaussian shapes for the density distribution, most of the integrals in calculating σ_R can be performed analytically which means that the evaluation of σ_R is numerically very simple.

The in-medium effects in NN cross section^10-13 at low and ntermediate energies is due to Pauli blocking, which prevents the scattered nucleons to go into occupied states in binary collisions between the projectile and target nucleons. The accurate treatment of in-medium effects is the geometric approach of Pauli blocking which needs numerical calculations of five fold integral to get σ_NN. Due to this complexity, many authors simplified this effect by assuming different approximations.^10-13 Recent expression for σ_NN was derived in Ref’s [1,9] which takes in-medium effects through density and energy dependence in σ _NN. When σ _NN (ρ) is determined from local matter density in each volume element of the nuclear overlap region, the value of σ_R is reduced by few percent compared with that obtained using free NN cross sectionσ ^f_NN [10,14]. This is because the constant effective global density ρ in σ_NN which produces the same value of ó_R as the more complicated correct treatment of density dependence is too small compared to the saturation nuclear matter density ρ = 0.17 fm^-3 [9]. Since the calculated value of σ_R is affected by several factors like the method of treating in-medium effects, rms radii of nuclei and range of NN force, it is needed to study the variation of σ_R with these factors.

The aim of the present work is to study the variation of the reaction cross-section at low and intermediate energies with different approaches of considering in-medium effects of σ_R .In this study we assume spherical shapes for both target and projectile nuclei and we consider different values of rms radius of the interacting nuclei. We use the recent density and energy dependent σ_NN derived in Ref.[9]. In the present study we first take σ_NN to be the free NN cross-section then we evaluate it at constant density value ρ =0.175 fm^-3. We compare the values of σ_R calculated by these two methods with the results obtained assuming local density variation in each volume element through the integration process.

The next section briefly describes the method of calculating σ_R using the optical limit of Glauber theory. The results and discussion are given in section -3.

Formulation

In the optical limit of Glauber theory, calculations of σ_R need a knowledge of the nuclear transparency T(b). This quantity is the probability that a projectile with impact parameter b will be transmitted through the target. Assuming purely absorptive and zero range approximation of the interacting nucleons, T(b) is given by

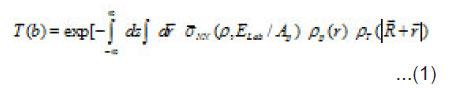
where 

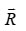
is the separation vector joining the centers of mass of the interacting nuclei and is the incident energy per projectile nucleon in the laboratory system. is the in-medium nucleon-nucleon cross-section at the given incident energy.

The iso-spin averaged NN cross section is evaluated at density value

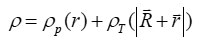
and averaged over the reaction cross sections of neutron-neutron,, proton-proton and neutron-proton, as

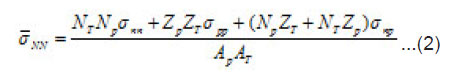
where A_P(T), Z_P(T) and N_P(T) are the projectile(target) mass, charge, and neutron numbers, respectively.

The reaction cross-section is obtained after integration of the nucleus-nucleus over all impact parameters as,

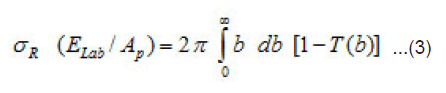
We assume that the density of the heavy spherical nuclei is given by the Fermi shape

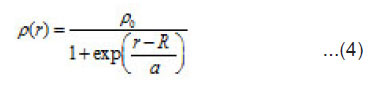
For light nucleus, we take the density parameters from Ref.[15]. The root mean square radius of the nucleus is defined by

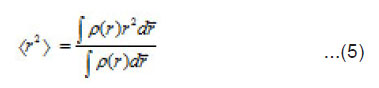
A correct parameterization of the cross-section between two free nucleons is given by Charagi and Gupta [1]. It depends on the incident nucleon energy in laboratory system as

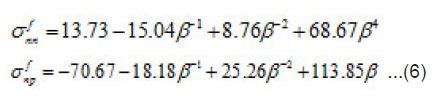
where

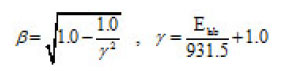
In-medium effects modify the free space cross-section in the following way,

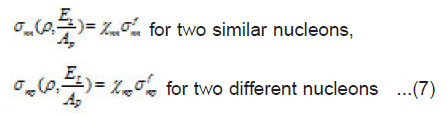
The multiplicative factors which take medium effects into consideration are given by [9],

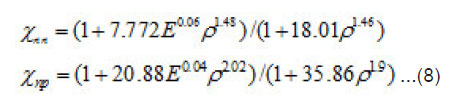
In using the last equations, the correct treatment of ρ–dependence is to take the density ρ as the sum of the projectile and target densities in each volume element. This corresponds to the local density at each point along the trajectory. Another approach to consider approximate medium effects is to evaluate at constant global density which is usually equal to the value of saturated nuclear matter density. In case of neglecting in-medium effects in calculating σ_R we use equations (6) for σ_NN instead of equations (7,8). In the present work the reaction cross-section is calculated for the light and heavy target pairs ¹²C-¹²C and ¹²C-²⁰⁸Pb at different values of incident energy per projectile nucleon in the range (10-1000 MeV/nucleon).

Results and Discussions

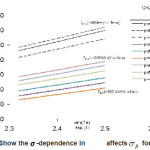
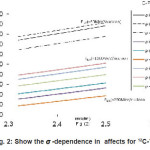
The aim of the present paper is to show the dependence of the reaction cross-section for light and heavy target nuclei on the method of treating in-medium effects in . For this purpose we calculate the reaction cross-section for the two pairs ¹²C-¹²C and ¹²C-²⁰⁸Pb. Fermi shape matter density distribution is assumed for the heavy target nucleus ²⁰⁸Pb. The calculations are done at different values of the incident energy per projectile nucleon, E_Lab/ A_p, and different values of rms radius of ¹²C-nucleus had been taken from 2.32 fm [16] to 2.5 fm [5]. In the present work the values of energy considered, start from 10 MeV/ nucleon up to 1000 MeV/ nucleon. In-medium effects are included in  

by considering local-variation of density in each volume element during the integration process, then, 

is calculated at global constant value of density. Also we calculated σ_R variation with energy using which corresponds to density value =0.0 fm^-3.

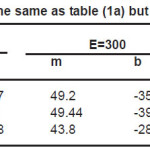
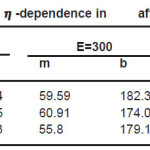
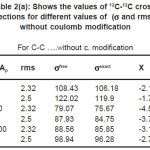
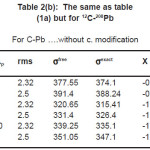
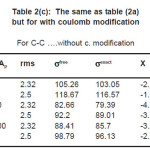
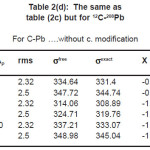
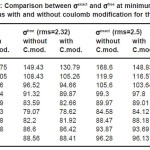
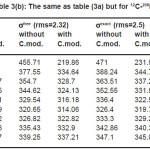
Fig’s (1), (2) and tables (1), (2) shows how the method used to treat ñ-dependence in affects, we present in tables (1) and (2) the values of for ¹²C and ²⁰⁸Pb target nuclei calculated by different methods and at different energy values. Each table contains the calculations of for two values of rms radius of ¹²C-nucleus. For light target nucleus, table (2a) shows that the percentage difference between σexct and is about 4.49 % and 3.75%, for rms values = 2.32 fm & 2.5 fm respectively at ELab/Ap =300 MeV/ nucleon. But for the heavy target nucleus the above differences are 1.66% and 1.53% for the same energies as shown in table (2b). In case of coulomb modification, for light target nucleus, table (2c) shows that the percentage difference between σ^exct and is about 4.11 % and 3.58%, for rms values = 2.32 fm & 2.5 fm respectively at E_Lab/A_p =300 MeV/ nucleon. But for the heavy target nucleus the above differences are 1.67% and 1.55% for the same energies as shown in table (2d).

Figure 1: Show the σ -dependence in affects σ_R  for 12C-12C

Click on image to enlarge

Figure 2: Show the σ -dependence in affects for 12C-12C

Click on image to enlarge

Table 1(a): The same as table (1a) but for 12C-208Pb

Click on image to enlarge

Table 1(b): show the η -dependence in affects σ_R for ¹²C-¹²C

Click on image to enlarge

Table 2(a): Shows the values of ¹²C-¹²C crosssections for different values of (σ and rms ) without coulomb modification

Click on image to enlarge

Table 2(b): The same as table (1a) but for 12C-208Pb

Click on image to enlarge

Table 2(c): The same as table (2a) but for with coulomb modification

Click on image to enlarge

Table 2(d): The same as table (2c) but for ¹²C-²⁰⁸Pb

Click on image to enlarge

At high E_Lab/A_p =1000 MeV/ nucleon for light and heavy target nucleus no change in the value of σ^exct in case of with and without coulomb modifications as shown (last row) in tables (3a,b).Tables(3a,b) represent also no change in the value of σ^free, it means that the coulomb repulsion is important at low incident energies without inmedium effect.

The coulomb interaction can affect the reaction cross-section especially at small energies. It deflects the projectiles away from the reaction region. It can be taken into consideration by modifying the trajectories using the equation

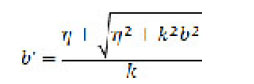
where η  is the sommerfield parameter given by  

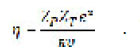
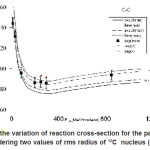
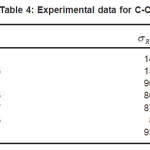
Table (4) show the experimental data for ¹²C-¹²C. From fig.(3) the value of decrease by increasing E_Lab/A_p until reached E_Lab/A_p =300 MeV/ nucleon (bottom) then increase gradually by increasing E_Lab/A_p. The experimental data gives good agreement with our results at low energy for rms = 2.32 and at high energy with rms =2.5.

Figure 3: Shows the variation of reaction cross-section for the pair 12C-12C. with (E_L/A_p) considering two values of rms radius of 12C nucleus (2.32& 2.5 fm)

Click on image to enlarge

Table 3(a): Comparison between σ^exact and σ^free at minimum rms and maximum rms with and without coulomb modification for the pair ¹²C-¹²C

Click on image to enlarge

Table 3(b): The same as table (3a) but for 12C-208Pb

Click on image to enlarge

Table 4: Experimental data for C-C

Click on image to enlarge

 References

1. S.K.charagi and S. K.Gupta, Phys, Rev. C 41: 1610 (1990).
2. R.J.Glauber Lectures in Theoretical Physics, edited by W.E.Britten et.al, (interscience, New York 1959)Vol. I, 315, W.Czyz and L. C. Mamximom, Ann Phys. (N. Y.) 52: 059 (1959).
3. J.A.Christley, and J.A.Tostevin, Phys. Rev. C59: 2309 (1999).
   CrossRef
4. S.John,L.W.Townsend,J.W.Wilson and R.K.Tripathi, Phys.Rev. C48: 766 (1993).
   CrossRef
5. S.Kox et al., Phys.Rev. C35, 1678 (1987), M.Buenerd et al., Nucl.Phys.A424, 313 (1984),and C.Perrin et al.,Phys.Rev.Lett.49, 1905 (1982).
   CrossRef
6. I.Tanihata et al., Phys. Lett. B. 206: 592 (1988), I.Tanihata et al., Phys. Lett. B. 160: 380 (1985), I.Tanihata et al., Phys. Rev. Lett. 55: 2676 (1985), I.Tanihata et al., Phys. Lett. B. 286: 261 (1992).
   CrossRef
7. J.W.Wilson et al., “Transport methods and interaction for space radiations” NASA Publications 1257 (1991).
8. M.Ismail, Aly Ellithi, H.Abu-Shady, Phys. Rev. C71: 027601 (2005)
9. Cai Xiangzhou, Feng Jun, Shen Wenqing, Ma Yugang, Wang Jiansong and Ye Wei Phys. Rev. C58: 572 (1998).
10. R.E.Warner, I.J.Thompson, and J.A.Tostevin Phys. Rev. C65: 044617 (2002).
    CrossRef
11. N.J.DI Giacomo, J.C.Peng, and R.M.Devries, Phys.Lett. 101B: 383 (1981).
    CrossRef
12. M.S.Hussien, R.A.Rego and C.A.Bertulaini, Phys. Rep. 201: 279 (1991).
    CrossRef
13. C.A. Bertulani, Phys. G. Nucl. Phys. 27: L67 (2001).
    CrossRef
14. M.Ismail, M.M.Osman, H.El-Gebaly, F. Salah and W. M. Seif, Phys. Rew. C 69: 014606 (2004).
15. G.F.Bertsch,B.A.Brown and H.Sagawa, Phys.Rev. C39: 1154 (1989).
    CrossRef
16. Jagar et al., Atomic Data, Nuclear Data Tables 14: 479 (1974).
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.