Views 
  

 Open Access -   Download full article: 

Vibrational Spectroscopic Study of Glycine Molecule

C. Yohannan Panicker1*, Hema Tresa Varghese2, Sheena Mary Y3, G. Krishnakumar4, B. Harikumar5, K. Raju3 and P. S. Amala Devi6

 

1Department of Physics, TKM College of Arts and Science, Kollam - 691 005, India. 

2Department of Physics, Fatima Mata National College, Kollam - 691 001, India.

3Department of Physics, Univeristy College, Thiruvananthapuram, India.

4Department of Physics, College of Engineering, Thiruvananthapuram, India.

5Department of Chemistry, TKM College of Arts and Science, Kollam - 691 005, India.

6Department of Physics, S.N.College, Chempazhanthy, Thiruvananthapuram, India.

DOI : http://dx.doi.org/10.13005/msri/070132

Article Publishing History
Article Received on : 15 Nov 2009
Article Accepted on : 20 Dec 2009
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:

The vibrational wavenumbers of glycine molecule were calculated using Gaussian03 software package at different levels and the fundamental modes are assigned. The predicted infrared and Raman activities are reported. The first hyperpolarizability is calculated and the glycine molecule is an attractive object for future studies of non linear optics. The calculated wavenumbers and geometrical parameters are in agreement with the reported experimental values.

KEYWORDS: Glycine; HF; DFT calculations; Hyperpolarizability

Copy the following to cite this article:

Panicker C. Y, Varghese H. T, Mary. Y. S. A, Kumar G. K, Harikumar B, Raju K, Devi P. S. A. Vibrational Spectroscopic Study of Glycine Molecule. Mat.Sci.Res.India;7(1)

Copy the following to cite this URL:

Panicker C. Y, Varghese H. T, Mary. Y. S. A, Kumar G. K, Harikumar B, Raju K, Devi P. S. A. Vibrational Spectroscopic Study of Glycine Molecule. Mat.Sci.Res.India;7(1). Available from: http://www.materialsciencejournal.org/?p=2306

Introduction

Amino acids, which constitute a very class of biomolecules, can act as potential oxygen and nitrogen donor ligands. It has been found that they utilize their functional groups as fully as possible in metal conduction.1 Copper(II) complexes of amino acids present important pharmacological interest as several of them show a wide spectrum of effects, including anti-inflammatory, antiulcer, anticonvulsant and even anittumoral activities.2-6 Summayya et al.7 reported the vibrational spectroscopic studies and ab initio calculations of L-glutamic acid 5-amide. Kumar et al.8 reported the vibrational spectrum of glycine molecule. In the present study, the wavenumbers of the title molecule and geometrical parameters are calculated theoretically at various computational levels and compared with the reported data.

Computational Details

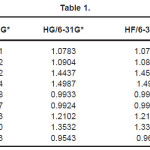
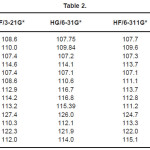
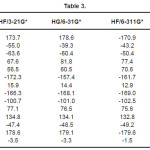
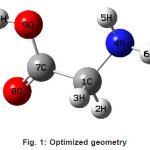
The vibrational wavenumbers were calculated using the Gaussian03 software package on a personal computer.9 The computations were performed at HF/6-21G*, HF/6-31G*, HF/6-311G* and B3LYP/6-31G* levels of theory to get the optimized geometry (Fig. 1) and vibrational wavenumbers of the normal modes of the title compound. DFT calculations were carried out with Becke’s three-parameter hybrid model using the Lee-Yang-Parr correlation functional (B3LYP) method. Molecular geometries were fully optimized by Berny’s optimization algorithm using redundant internal coordinates. Harmonic vibrational wavenumbers were calculated using analytic second derivatives to confirm the convergence to minima in the potential surface. The DFT hybrid B3LYP functional tends also to overestimate the fundamental modes; therefore scaling factors have to be used for obtaining a considerably better agreement with experimental data. Thus, a scaling factor of 0.9613 has been uniformly applied to the B3LYP and 0.8929 for HF methods calculated wavenumbers.10 The observed disagreement between theory and experiment could be a consequence of the anharmonicity and of the general tendency of the quantum chemical methods to overestimate the force constants at the exact equilibrium geometry. The obtained geometrical parameters are given in Tables 1-3.

Table 1

Table 1
Click on image to enlarge

Table 2

Table 2
Click on image to enlarge

 Table 3

Vol7_No1_Vib_Yoh_tab3
Click on image to enlarge

 Figure 1: Optimized geometry

Figure 1
Click on image to enlarge

Results and Discussion

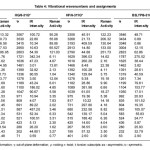
The calculated (scaled) wavenumbers and assignments are given in Table 4. In associated aliphatic and alicylcic primary amines11, the NH2 asymmetric stretching vibration occurs at 3365±25  cm-1 and symmetric stretching vibtration in the region 3290± 30 cm-1. In the vibrational spectra of copper complexes of L-asparagine and L-glutamine the υasNH2 is reported at 3265, 3296, 3278 cm-1 in the IR spectrum.12 The NH2 scissoring vibration13 give rise to a broad band in the region 1600±50 cm-1. According to Roeges13 the rocking/twisting NH2 mode is expected in the region 1160 ± 140 cm-1. In aliphatic amines this mode is mixed with the methylene twist and also with the C-N stretching vibration. Associated α-saturated primary amines show a characteristic very broad diffuse ùNH2 band between 1000 and 700 cm-1, with a maximum absorption at 840 ± 55 cm-1. The NH2 torsion14,15 is expected in the region 290 ± 130 cm-1. Kumar et al.8 reported the NH2 vibrations at 3414, 1610, 1334, 893, 698 cm-1 in the IR spectrum, 1323, 893, 697 cm-1 in the Raman spectrum and at 3396, 1673, 1342, 897, 720 cm-1 theoretically.

Table 4: Vibrational wavenumbers and assignments

Table 4
Click on image to enlarge

The –C(=O)OH group is best characterized by the OH stretch, the C=O stretch and the OH out-of-plane deformation and even by the C-O stretch and the OH in-plane deformation. The C=O stretching vibration in the spectra of carboxylic acids give rise to a strong band in the region 1725 ± 65 cm-1. The OH in-plane deformation, coupled to the C=O stretching vibration, is expected in the region 1390 ± 55 cm-1. The C(=O)O stretching vibration, coupled to the OH in-plane deformation16 exhibits a moderate band in the region 1250 ± 80 cm-1. The out-of-plane Oh deformation16 is expected in the region 905 ± 65 cm-1. The C=O in-plane deformation is active in the region 725 ± 95 cm-1 and the out-of-plane C=O deformation in the region16 595 ± 85 cm-1.

The vibrations of the CH2 group, the asymmetric stretching, symmetric stretching, scissoring vibration and wagging vibration appear in the regions 3000 ± 50, 2965 ± 30, 1455 ± 55 and 1350 ± 85 cm-1, respectively.13,17 The twisting and rocking modes of CH2 are expected13 around 1280 and 850 cm-1. The torsional modes of CH2 are seen in the low wavenumber range.13 Baran et al.18 reported the CC stretching bands in the range 870-1117 cm-1 and CC bending modes below 400 cm-1. For glutamic acid dipeptide the CC stretching mode19 is reported in the region 910-1090 cm-1 and the bending modes in the range 109-399 cm-1. Kumar et al.8 reported the CH2 vibrations at 3084, 2920, 1410, 504 cm-1 in the IR spectrum, 3050, 2930, 1410, 497 cm-1 in the Raman spectrum and at 2948, 2915, 1458, 487 cm-1 theoretically. 

Kumar et al.8 reported the bond lengths in the ranges C1-N4 =1.431-1.473Å, C7=O8 = 1.2-1.234Å, C7-O9 = 1.34-1.36Å, O9-H10 = 0.94 -1.00Å and N-H = 0.99-1.001Å which are in agreement with our calculated bond lengths. The reported values8 of the bond angles N4-C1-C7 = 109.9-115.9º, C1-C7-O8 = 125.4-128.8º, C1-C7-O9 = 110.6-114.0º and the dihedral angles O8-C7-C1-N4 = 141.5º, O9-C7-C1-N4 = -40.5º and C1-C7-O9-H10 = -178.5º and these values are in agreement with our results.

Analysis of organic molecules having conjugated π-electron systems and large hyperpolarizability using infrared and Raman spectroscopy has evolved as a subject of research.20 The first hyperpolarizability (β0) of this novel molecular system is calculated using theoretically, based on the finite field approach. In the presence of an applied electric field, the energy of a system is a function of the electric field. First hyperpolarizability is a third rank tensor that can be described by a 3×3×3 matrix. The 27 components of the 3D matrix can be reduced to 10 components due to the Kleinman symmetry.21 The calculated first hyperpolarizability of the title compound is 0.4910-30, 0.5110-30, 1.1210-30, 0.5410-30 esu for HF/ 3-21G*, HF/6-31G*, HF/6-311G* and B3LYP/6-31G* methods. We conclude that the title compound is an attractive object for future studies of non linear optical properties.

References

  1. Ho, B.Y.K., Zubieta, J.A., and Zuckerman,J.J., J. Chem. Soc. Chem. Commun. 2: 88 (1975).
  2. Sorenson, J.R.J, J. Med. Chem. 19: 135 (1976).
  3. Sorenson, J.R.J., in: Sigel, H., (Ed.) Metal Ions in Biological Systems, Marcel Dekker, New York (1982).
  4. Baran, E.J., Acta Farm. Bonaerense 4: 125 (1985).
  5. Farrell, N., Transition Metal Comlexes as Drugs and Chemotherapeutic Agents, Kluwer, Dordrechi (1989).
  6. Baran, E.J., Mini Rev. Med. Chem. 4: 1 (2004).
  7. Sumayya, A., Panicker, C.Y., Varghese, H.T., and Harikumar, B., Rasayan J. Chem. 1: 548 (2008).
  8. Kumar, S., Rai, A.K., Singh, V.B., and Rai, S.B., Spectrochim. Acta 61A: 2741 (2005).
  9. Frisch, M.J., et al., Gaussian03, Revision C.02., Gaussian Inc., Wallingford, CT (2004).
  10. Foresman, J.B., in: Frisch, E., (Ed.), Exploring Chemistry with Electronic Structure Methods: A Guide to Using Gaussian, Pittsburg, PA, (1996).
  11. Segal, L., and Eggerton, F.V., Appl. Spectrosc. 15: 112 (1961).
  12. Baran, E.J., Viera, I., and Torres, M.H., Spectrochim. Acta 66: 114 (2007).
  13. Roeges, N.P.G., A Guide to the Complete Interpretation of Infrared Spectra of Organic Structures, Wiley, New York (1994).
  14. Craven, S.M., and Bentley, F.F, Appl. Spectrosc. 26: 449 (1972).
  15. Craven, S.M., Bentley, F.F., and Pensenstadler, D.F., Appl. Spectrosc. 26: 647 (1972).
  16. Fischmeister, I., Spectrochim. Acta 20: 1071 (1964).
  17. Colthup, N.B., Daly, L.H., and Wiberly, S.E., Introduction to Infrared and Raman Spectroscopy, second ed., Academic Press, New York (1985).
  18. Baran, E.J., Viera, I.,  and Torres, M.H.,Spectrochim. Acta 66: 114 (2007).
  19. Navarrete, J.T.L., Hernandez, V., and Ramirez, F.J., J. Mol. Struct. 348: 249 (1995).
  20. Tommasini, M., Castiglioni, C., Del Zoppo, M., and Zerbi, G., J. Mol. Struct. 480: 179 (1999).
  21. Kleinman, D.A., Phys. Rev. 126: 1977 (1962).
Share Button

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

Designed by: Designtohost
Copyright © 2024 MSRI