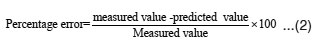Empirical Models for Estimating Properties of Developed Composite Material from Agro Waste

J. O. Osarenmwinda* and J. C Nwachukwu

Department of Production Engineering, University of Benin, Benin City, Nigeria.

Corresponding Author E-mail: joosarenmwinda@yahoo.com

DOI : http://dx.doi.org/10.13005/msri/070204

ABSTRACT:

Study was carried out to develop an empirical models for estimating the properties of developed composite material from agro waste (sawdust and palm kernel shell). The properties of the produced composite materials from agro waste obtained in previous experimental investigation were used to determine empirical model for hardness, yield strength, ultimate tensile strength, modulus of elasticity; modulus of rupture, internal bond strength, density, thickness swelling and water absorption .The values obtained from the empirical models were found to compare favourably with the experimental values. The mean percentage error were determined to be -0.02167% (hardness), -0.462167%( yield strength),-0.03625 (ultimate tensile strength), -0.01045% (modulus of elasticity), -0.044057% (modulus of rupture), 0.001033% (internal bond strength),0.2153%(density), 0.5277% (thickness swelling) and 0.1365% (water absorption). These values were insignificant and below the maximum recommended error of 10%. These model performance were therefore found to be satisfactory and show good predictability.

KEYWORDS: Agro waste; Composite material; Empirical model; Validity

Copy the following to cite this article: Osarenmwinda J. O, Nwachukwu J. C. Empirical Models for Estimating Properties of Developed Composite Material from Agro Waste. Mat.Sci.Res.India;7(2)

Copy the following to cite this URL: Osarenmwinda J. O, Nwachukwu J. C. Empirical Models for Estimating Properties of Developed Composite Material from Agro Waste. Mat.Sci.Res.India;7(2). Available from: http://www.materialsciencejournal.org/?p=2364

Introduction

In the past twenty years, materials research and development (R&D) has shifted from monolithic to composite materials, adjusting to the global need for reduced weight, low cost, quality, and high performance in structural materials.¹ The demand for new materials with higher specifications led to the concept of combining different materials in an integral-composite one. Such composite materials result in performance that cannot be attained by the individual constituents. An additional advantage is that composite offer flexibility in design.²

A lot of researchers have developed models for estimating properties of composite. Chunping et al.,³ carried out a study aimed to model fundamental bonding characteristics and performance of wood composite. In their work, a mathematical model and a computer simulation model were developed to predict the variation of inter-element (strand) contact during mat consolidation. The mathematical predictions and the computer simulations agree well with each other. Their results showed that the relationship between the inter-element contact and the mat density was highly nonlinear and was significantly affected by the wood density and the element thickness. Certain mechanical properties of composite panels were observed by Harless et al,⁴ to depend on the density variations that occur through the panel thickness. They then proposed an analytical tool to predict density profile as a function of the manufacturing processes. A multilayer description of the density and moisture gradients resulting from the felting process provided input for the model. Inputs for the pressing process included platen temperature and press closing rate. The model they developed simulated the physical and mechanical processes that occur in the press and mat system. Carldon and Matunana⁵ constructed a response surface model using a Box-Behnken design to statistically model and optimize the material compositions-processing conditions-mechanical property relationships of formaldehyde-free wood composite panels. Three levels of binding agent content, pressing time, and press temperature were studied and regression models were developed to describe and optimize the statistically effects of the formulation and processing conditions on the mechanical properties of the panels. They observed that linear models best fit both the modulus of rupture (MOR)) and internal bond (IB) strength of the panels. Flexural stiffness (modulus of elasticity (MOE)) was best described by a quadratic regression model.

The development of a two-dimensional mathematically model to describe the internal conditions during the hot-compression of wood-based composite panels was carried out by Zombori et al [6]. Five primary variables were considered during the model development air content. Vapor content, bound water content, and temperature within the mat, and the extent of the cure of the adhesive system characterized by the cure index. The mathematical model they developed predicted temperature, moisture content, partial air and vapour pressures, total pressure, relative humidity and extent of adhesive cure within the mat structure under a typical hot-compression process. Adeyemi and Adeyemi,⁷ developed empirical formulas, based on the diffusion model and the drying data (i.e moisture ratios, with drying times) of the composite from sawdust were computed and presented for various curing temperature and at different percentages of hardener resin addition. There were a number of studies on moisture transfer modeling of wood, but no systematic study for moisture transfer in board with respect to usage or storage.⁸ The physical parameters of four kinds of composite boards were determined by them in this study. The unsteady-state diffusion coefficients and surface emission coefficients of moisture in boards were separated in one experimental period by using the method of linear regression. Then the moisture transfer processes in board were analyzed by using Finite Element Method (FEM), and the moisture absorption processes of four kinds of boards were observed experimentally. By comparing the computed results with the experimental results, it showed that the error was within 10%. Therefore, they came to the conclusion that the processes of moisture transfer in board can be described by using FEM. kruse et al,⁹ set out to develop a model for the production process of composite by using regression analyses to estimate the predication quality of process models. They found that, when considering parameters solely under the viewpoint of statistical requirements, the resulting process models turn out too optimistic. Therefore, creating process models requires a pre-selection of process parameters under a technological point of view in order to reduce their number to a level commensurate with a meaningful statistical calculation. They concluded that process models developed in this way allowed the prediction of Internal Bond(IB). IB proved to be determined primarily by the particle dimensions of the core, resin pH, particle MC, production speed, and various hot-press parameters.

Repeatedly altering a commercial composite board manufacturing process to produce a predetermined properties was observed to be undesirable from economic and production standpoints [ 4,10]. There also seems to be lack of an empirical model to predict properties of composite materials from agro waste in particular composite from sawdust and palm kernel shell combination. This study therefore focuses of the development of empirical model making use of previously obtained experimental data to estimate properties of produced composite material from agro waste(sawdust and palm kernel shell). This models it is hoped will help and serve as a guide for researchers, industrialist and small-scale manufacturers involved in composite material production.

Material and Methods

Materials

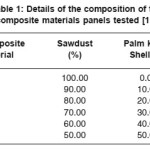
Sawdust from mahogany and palm kernel shell used to produced the composite material were obtained from Benin City, Edo State, Nigeria, while urea formaldehyde was used as binder.

Method

Composite Material Production

The palm kernel shell was ground to granules using Jaw crushing machine. The palm kernel shell granules and sawdust were first air dried in the sun and latter transferred separately to an electric oven and dried at 105⁰C. It was continuously monitored until moisture content of about 4±0.2% was obtained .The sawdust and ground palm kernel shell were screened separately with sieves of appropriate size to particle size of 300µm diameters using vibrating sieve machine. Urea formaldehyde was prepared by mixing thoroughly with water in ratio 3.5:1 parts, before being mixed with appropriate percentage of saw dust/palm kernel shell mixture as shown in the experimental design for the production of composite material in Table 1 [10].The panels to be produced was with particle size of 300µm and Urea formaldehyde binder concentration of 20% of the oven dry weight of agro waste [10,11]. The prepared binder was then blended with the weighted sawdust to palm kernel shell in appropriate proportion to ensure an efficient and proper coating of the agro waste with the binder. The mixture was later poured into a mould measuring of 330 x 110 x 30mm and hot pressed at a temperature of 200⁰C and a pressure of 26.5 kg/cm². Composite panel was produced according to the ratio in Table 1. The test pieces were exposed for four days (96 hours) in an air conditioned room at a temperature of 20 + 3^oC and relative humidity of 65 + 1% to obtain constant weight [12].

Table 1: Details of the composition of the composite materials panels tested [10]

Click on image to enlarge

The Composite materials were evaluated for the following properties: thickness swelling (24hr immersion), water absorption (24hr immersion), modulus of rupture , modulus of elasticity , hardness, density, yield strength and ultimate tensile strength and Internal bond according to European Norm (EN) specifications [13,14,15].

Model Formulation :In this work all empirical model was developed using the values obtained from previous experimental investigation for composite material properties [10]. The empirical model was used to predict the properties of the composite material taking the inputs as percentage sawdust composition and percentage palm kernel shell composition respectively. The empirical model was developed using “MATHMATICAL PRODUCT“ software program expressing the outputs in the quadratic form as shown in Equation 1

Output = a₀ + a₁x+ a₂x²+ a₃ y+ a₄ y² …(1)

Where the input are as follows: x and y are sawdust composition and palm kernel shell composition in percentages respectively and a₀, a_1, a_2, a₃ ,a₄ are constants.

The outputs are as follow: hardness (HRc),yield strength(N/mm²),ultimate tensile strength(N/mm²), modulus of elasticity (N/mm²), modulus of rupture(N/mm²), internal bond strength (N/mm²),density (Kg/m³), thickness swelling (%) and water absorption (%) respectively.

Percentage Error

The percentage error was determined using Equation 2

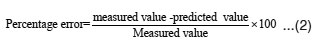
The assumptions made in this model are as follows

The composite was of sawdust and palm kernel

The test binder was  Urea formaldehyde applied at a concentrations of 20% (percentage of oven dry weight of agro waste) throughout the study.

Only agro waste (sawdust and palm kernel shell) particle size of 300µm was used .

All the composite production parameters were kept constant except composite agro waste constituent (sawdust and palm kernel)

Results and Discussion

Developed Empirical Model

The empirical models developed are as shown in Equations 3 -11.They are as follow: 

Hardness= –19.7016 – 0.344849x – 0.00511875x² + 0.076577y- 0.00125447y² …(3)

Yield strength = –1.01189 + 0.006555x -0.0000584226x²+ 0.0680746y – 0.0043363y² …(4)

Ultimate tensile strength= –1.56324 + 0.0114774x- 0.0000353483x²+ 0.0964542y + 0.000354991y²…(5)

Modulus of elasticity = 741.366 + 6.99665x+0.015754x²+ 35.716y – 0.128611y² …(6)

Modulus of rupture= –3.94653 + 0.0381715x +0.000152525x²+ 0.184151y + 0.000395689y² …(7)

Internal bond strength=0.15064 + 0.0015024x +0.00000594036x²+ 0.0067673y – 0.0000148689y²…(8)

Density =252.2 + 2.98596x + 0.0260344x²+8.254722y + 0.0452549y² …(9)

Thickness swelling = 3.68561 + 0.0741048x +0.00127468x²– 0.0762456y + 0.00122683y²…(10)

Water absorption = 8.97721 + 0.149617x +0.00204826x²+ 0.0136251y – 0.00122683y²…(11) 

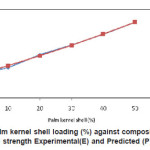
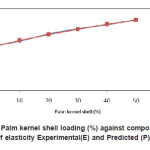
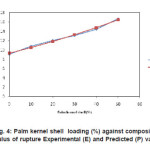
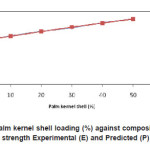
The plot of Experimental values(E), and Predicted values(P) against constituent composition(palm kernel shell %) for hardness ,yield strength, ultimate tensile strength, modulus of elasticity, modulus of rupture, internal bond strength ,density , thickness swelling and water absorption are shown in Figures. 1-9 respectively.

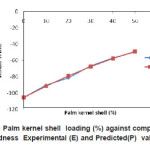
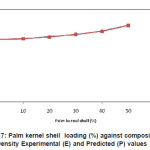
Figure 1: Palm kernel shell loading (%) against composite Hardness Experimental (E) and Predicted(P) values

Click on image to enlarge

Figure 2: Palm kernel shell loading (%) against composite yield strength Experimental (E) and Predicted (P) values

Click on image to enlarge

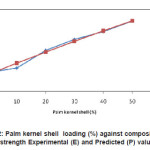
Figure 3: Palm kernel shell loading (%) against composite ultimate tensile strength Experimental(E) and Predicted (P) values

Click on image to enlarge

Figure 4(a): Palm kernel shell loading (%) against composite Modulus of elasticity Experimental(E) and Predicted (P) values

Click on image to enlarge

Figure 4(b): Palm kernel shell loading (%) against composite Modulus of rupture Experimental (E) and Predicted (P) values

Click on image to enlarge

Figure 6: Palm kernel shell loading (%) against composite Internal bond strength Experimental (E) and Predicted (P) values

Click on image to enlarge

Figure 7: Palm kernel shell loading (%) against composite Density Experimental (E) and Predicted (P) values

Click on image to enlarge

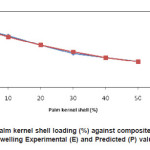
Figure 8: Palm kernel shell loading (%) against composite thickness swelling Experimental (E) and Predicted (P) values

Click on image to enlarge

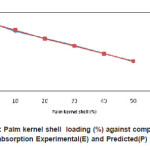
Figure 9: Palm kernel shell loading (%) against composite water absorption Experimental(E) and Predicted(P) values

Click on image to enlarge

Accuracy and Validity of Model

The model was validated by comparing the predicted values with experimental values. The predicted values were found to compare favourably with experimental values (see fig.1-9). The mean percentage error determined using Eqn. 2 were found to be -0.02167% (hardness), -0.462167%( yield strength),-0.03625 (ultimate tensile strength), -0.01045% (modulus of elasticity), – 0.044057% (modulus of rupture), 0.001033% (internal bond strength),0.2153%(density) 0.5277% (thickness swelling) and, 0.1365% (water absorption)respectively. These values are insignificant and below the maximum error of 10% proposed by Liping and Deku [8]. These values were therefore found to be satisfactory and show good predictability of the model. The empirical model developed are reasonably accurate to predict properties of composite material from agro waste and will serve as useful guide for researchers, industrialist and small-scale materials manufacturers.

Conclusion

The empirical model developed are reasonably accurate to estimate mechanical and physical properties of composite material from agro waste(sawdust and palm kernel shell). The model performance were found to be satisfactory and show good predictability. The empirical models and software developed using visual basics for computing predicted composite materials properties from model will be useful and serve as guide for researchers, industrialist and small-scale materials manufacturers.

References

1. Ejiofor J.U and Reddy R.G, Developments in the Processing and Properties of particulate Al-Si Composites . JOM 49(11): 31-37 (1997).
2. Gasser F.A, A three-phase constitutive model for macrobrittle fatigue damage of composites. A PhD Dissertation Submitted to College of Engineering and Mineral ResourcesatWestVirginia University, Department of Mechanical and Aerospace Engineering Morgantown, West Virginia.pp 1-5 (2000)
3. Chunping, D. , Y .Changing and Z. Cheng, Theoretical modeling of bonding characteristics and performance of wood composites:part 1.inter –element contact. Journal of wood and fiber science., 39(1): 48 -55 (2007).
4. Harless, T. E. G., F. G. Wagner, P. H. Short, R. D. Seale, P. H. Mitchell, and D. S. Ladd., A model to predict the density profile of particleboard. Wood and Fiber Sci. 19(1):81-92 (1987).
5. Carlborn K and L. M. Matuana, Modeling and optimization of formaldehyde-free wood composites using a Box-Behneken design. Polym. compos., 27: 497-503 (2006).
6. Zombori B.G,F .A Kamke and L .T Watson, Wood and fiber science 35(1): 2-23 (2003).
7. Adeyemi, S.O. and M.B Adeyemi, Curing temperature and hardener resin addition affecting  drying  and  properties of particleboards. Int. J. of Materials and Product Technology., 17(7): 590-599 (2002).
8. Liping, C, S. Deku , Modeling of the moisture transfer process in particleboards. Holz als Roh-und Werkstoff. 50(10): 395-399 (1992).
9. Kruse, K., H. Thomen , H.Maurer, A. Steffena, R. Leon–Mendez, Optimization of particleboard production by means of process modeling. Hotz Roh-werkst., 55(1): 17-24 (1997).
10. Osarenmwinda, J.O, Development of composite material from agro waste for industrial and domestic application. PhD Thesis, Department of Production of Engineering, University of Benin, Benin city, Nigeria (2009).
11. Osarenmwinda J.O and J.C Nwachukwu, Effect of particle size on some properties of Rick husk particle board. Advanced Materials Research, Trans Tech Publications Ltd, Switzerland., 18-19: 43-48 (2007).
12. Nemli, G., S. Samet Demirel, E. Gümüºkaya, A. Aslan and C Acar,. Feasibility of incorporating waste grass clippings (Lolium perenne L.) in particleboard composites. Waste Management, 29(3): 1129-1131 (2009).
13. EN 310. Wood based panels, Determination of modulus of elasticity in bending and bending strength. European standardization committee, Brussells (1993).
14. EN 317. particleboards and fiberboards determination of swelling in thickness after immersion, European Standardization committee, Brussels (1993).
15. EN 319 . Particleboards and fiberboards determination of tensile strength perpendicular to plane of the board. European standardization committee, Brussels (1993).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.