Views 
   PDF Download PDF Downloads: 820

 Open Access -   Download full article: 

Investigation of Deuteration Effect on Sound Attenuation in Hydrogen Bonded Ferroelectric Crystals

S. C. Deorani, P. Singh and M. S. Yadav

R.R. Autonomous College, Alwar - 301 001, India.

DOI : http://dx.doi.org/10.13005/msri/080120

Article Publishing History
Article Received on : 24 Mar 2011
Article Accepted on : 20 Apr 2011
Article Published :
Plagiarism Check: No
Article Metrics
ABSTRACT:

The anomalous ultrasonic attenuation of longitudinal wave propagated in KDP and DKDP have been discussed and calculated near Curie-temperature (Tc) in Para- electric phase in the frequency range 5 to 50 MHz. The attenuation of longitudinal waves is primarily due to a strong interaction with thermally excited phonon in the coupled-soft mode. Temperature and frequency variations of attenuation are discussed. Anharmonicity in the crystal potential is essential to discuss (observe) critical attenuation.

KEYWORDS: Attenuation; Coupled-soft mode; Dyson's equation; Fourier transform; Green's function; Phase transition and isotope effect.

Copy the following to cite this article:

Deorani S. C, Singh P, Yadav M. S. Investigation of Deuteration Effect on Sound Attenuation in Hydrogen Bonded Ferroelectric Crystals. Mat.Sci.Res.India;8(1)

Copy the following to cite this URL:

Deorani S. C, Singh P, Yadav M. S. Investigation of Deuteration Effect on Sound Attenuation in Hydrogen Bonded Ferroelectric Crystals. Mat.Sci.Res.India;8(1). Available from: http://www.materialsciencejournal.org/?p=2523

Introduction

By ultrasonic measurements, static and dynamic properties of the crystal can be measured simultaneously. Ultrasonic attenuation data provide information about the dynamic behavior and from the frequency as well as temperature dependences, the mechanism involved can be understood.

Coupled-soft mode (mixed tunneling proton-optical phonon mode) frequency, is held responsible for the anomalous behavior of the hydrogen bonded ferroelectrics when T→Tc. As T→Tc, the coupled-soft mode frequency [Ω2 = k (T-Tc)] becomes small, resulting in an increase of its amplitude and sound mode couples strongly with the coupled-soft mode. This anomalously large amplitude of coupled-soft modes should influence the acoustic mode via phonon-phonon interactions and is expected to give rise to an anomalous behavior of sound waves near Tc. These sound modes are longitudinal acoustic modes as in the vicinity of Tc, only the interactions of longitudinal sound remains. The interaction between transverse acoustic and transverse optic modes is very small so that the expressions for attenuation and velocity would not show any abrupt changes.

The H-D isotope effects in hydrogen bonded ferroelectrics like KDP (KH2 PO4) are well known in solid state physics.1-11 Litov and Uehling12 have clearly shown such an acoustic anomaly at Tc. KDP is a uniaxial ferroelectric with a Curie-temperature Tc = 122 K and 222 K for its analogous deuterated isomorph DKDP (KD2PO4). The ferroelectric phase transition in KDP is of first order. In Para-electric phase KDP is tetragonal and the xy mechanical strain is piezoelectrically coupled to the polarization along the ferroelectric z- axis. Therefore, the anomalous ultrasonic wave is a transverse wave propagating in the [100] direction with its polarization in the [010] direction.

Approaching Tc from above, the acoustic attenuation increases and the acoustic velocity decreases due to piezoelectric coupling between the elastic strain and the electric polarization. For uniaxial ferroelectrics with soft acoustic modes, critical fluctuations can be suppressed by the long range interactions associated with piezoelectric coupling between electric polarization and elastic strain. The traditional microscopic theory for ferroelectric phase transition in KDP family is based on an Order–disorder model that considers proton tunneling between two sites of adjacent tetrahedra.13

In KDP crystals the bilinear coupling between the proton system and the optical phonon plays an essential part in ferroelectric phase transition. The presence of a coupled soft mode involving the optical phonon and the collective tunneling mode of the protons is investigated in KDP.10

In this paper, we will investigate the isotope effect on sound attenuation in KDP in para phase as a function of temperature and frequency in presence of anharmonicity and will compare the results with the available results. In section 2, frequency and temperature variation of critical attenuation are numerically calculated. In section 3 and 4, the results are compared and discussed with experimental data available.

Calculation

Variation Of Sound Attenuation With Temperature

For attenuation of sound waves, we consider the following Green’s function for acoustic phonons,

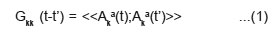
equation 1

The modified Hamiltonian used in this study is similar to as used by Naithani et.al.14 With the help of modified model Hamiltonian, Fourier transform and writing equation of motion for Green’s function (1) in Dyson’s equation form, one gets

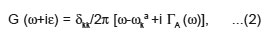
equation 2

Where ΓA is damping constant for acoustic phonons in presence of anharmonicity. The coupled-soft mode frequency is stabilized in the presence of anharmonicity. The attenuation constant is given by

equation 3

Where damping constant is given by equation (3) of our earlier reference,15 c is the sound velocity. In the vicinity of Tc temperature dependence of αa(ω) or αc can be expressed as

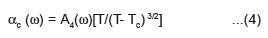
equation 4

Here A4 (ω) is fourth-order anharmonic interaction term.

It is clear from equation (4) that when T→ Tc the attenuation constant increases anomalously. Raw attenuation data for longitudinal sound wave propagation in KDP and DKDP in the [100]  direction are shown in figures (2) and (4) in references 1 and 2 respectively.

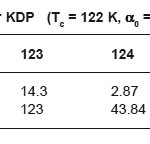
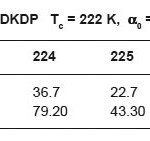
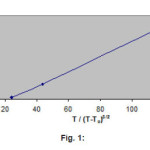
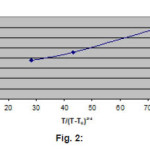
In this study, only the net critical relaxation attenuation (αc ) near structural phase transition is pertinent, so that the remaining attenuation, by extrapolating from the attenuation at higher temperature, should be subtracted as a background. The background attenuation (α0) is small, frequency independent and temperature insensitive. Extrapolated values of αc with T/(T-Tc)3/2 are given in table 1 for KDP and in table 2 for DKDP with the help of references.1,2 In figure 1, αc vs T/(T-Tc)3/2 is plotted for KDP and in figure 2 for DKDP respectively for 15 MHz frequency which are linear, in agreement with our theoretical results in equation (4). It is also clear from equation (4) that when T→Tc, attenuation constant becomes anomalously large in agreement with the results of others.16,17

The power law αc vs T/(T-Tc)3/2 is found to be for the reduced temperature t = (T-Tc)/Tc between 0.008 and 0.025 for α0= 0.7 dBcm-1 for KDP1 and t=0.009 and 0.018 with α0= 1.3 dBcm1 for DKDP2. A4 (ω)= 8.13x 10-3 dBcm-1K1/2 (KDP) and A4(ω)= 3.7x 10-1 dBcm-1K1/2 (DKDP) are obtained from the references1,2 by curve fitting 

Variation of sound attenuation with frequency

Previously,15 we have expressed attenuation as

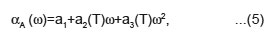
equation 5

Where ω2 dependence arises from the quartic anharmonic interactions while ù dependence is due to the cubic anharmonic interactions term. If we retain quartic anharmonic interaction terms (as a3 > a2 for stabilization of coupled- soft mode near Tc), we have

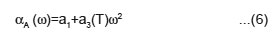
equation 6

Comparing this equation with equation α = αo + αc, we get αo = a1 (background attenuation) and

equation 7

The parameter a3 is calculated by best fitting of data obtained from figure 2 of reference 1 to equation (7) at T= 123 K at frequency 15 MHz for KDP and figure 4 of reference 2 to equation (7) at T=226 K at frequency 15 MHz for DKDP.

This gives
a3 = 1.9198 × 10 -15dBs2cm-1
And
αc = 7.5714 × 10-2 f2 dBcm-1 for KDP and
a3 = 1.1823 × 10 -15dBs2cm-1
And
αc = 4.663 × 10-2 f2 dBcm-1 for DKDP

Where f (5-50MHz) is in MHz. This investigation shows that ω2 dependence is in agreement with the results of Toda et.al..18

Table 1: For KDP  (Tc = 122 K, α0 = 0.7 dBcm-1)

table 1
Click on image to enlarge

Table 2: For DKDP Tc = 222 K, α0 = 1.3 dBcm-1

table 2
Click on image to enlarge

Figure 1

figure 1
Click on image to enlarge

Figure 2

figure 2
Click on image to enlarge

Discussion

Damping constant ΓA(ω) of the acoustic phonon decreases, if the damping of the coupled-soft mode, which interacts with the acoustic mode increases . It is obvious that in Order-disorder
ferroelectrics, the attenuation of sound waves varies as T/(T-Tc)3/2 in Para-electric phase near Tc. The ω2 as well as (T-Tc)-3/2 power laws are in agreement with the results of others.19-23 Anharmonicity A4 (ω)) is necessary in the crystal to observe these dependences.

At constant temperature, attenuation in DKDP with increasing frequency is less than in KDP. The law αA (ω) α T/(T-Tc)3/2 can be valid to a good approximation to study acoustic properties quantitatively. Attenuation does not obey a simple power law (T-Tc)n. In the low frequency (ultrasonic frequency) regime (ωτ << 1), the critical sound attenuation (equation 7) is in agreement with the results of Hu et al17 where αc = α – α0 =ω2 τ (c066-c66)/2uc066 .

Conclusion

An expression is derived for attenuation constant of sound and its temperature and frequency variations are discussed in KDP and DKDP using double time thermal Green’s function technique. In the Hamiltonian, mass and force constant changes due to deuteration are taken into account in the crystal Hamiltonian augmented with forth-order anharmonic term and higher order electric moment terms and their contributions to scattering processes. The scattering processes operate for relaxation times for a particular acoustic phonon mode. The acoustic width in the phonon frequencies is temperature dependent giving the temperature dependence of the attenuation constant. The temperature dependence is the direct consequence of the anharmonicity in the crystal potential. 

In the vicinity of Curie-temperature, the coupled-soft mode frequency (ω00) which is imaginary in harmonic approximations becomes stabilized and temperature dependent due to anharmonic terms and becomes vanishingly small and No (equation 3 of reference 15) becomes anomalously large and hence, the attenuation constant increases anomalously. The treatment adopted here leads one to see the comparative variations of the sound attenuation in KDP and DKDP with temperature and frequency parameters in Para phase.

Acknowledgements

One of the authors SCD is thankful to UGC for providing financial assistance.

References

  1. Litov E. and Garland C. W. Phys. Rev. B2: 4597 (1970).
    CrossRef
  2. Takada S. et al. Prog. Theor. Phys. 53: 936 (1975).
    CrossRef
  3. Fuji K. et al. J. Phys. Soc. Jpn. 61: 342 (1992).
    CrossRef
  4. Kawashita Y. and Tominaga Y. Solid State Comm. 145: 218 (2008)
    CrossRef
  5. Ichikawa M. Chem. Phys. Lett. 79: 583 (1981); Acta Cryst. B 34: 2074(1978)
    CrossRef
  6. Merunka D. and Rukvin B. Physica B391: 28 (2007)
    CrossRef
  7. Wesselinowa J. M. Phys. Stat. Sol. (b)139:329 (1987)
    CrossRef
  8. Blinc R. and Jeks B. J. Phys. C: Solid State  Phys. 15: 4661 (1982)
    CrossRef
  9. Matshushita E. and Matsubara T., Prog. Theor. Phys. 67: 1 (1982)
    CrossRef
  10. Tokunaga M. and Tatsuzaki I. Phase transitions 4: 97 (1984)
    CrossRef
  11. Upadhyay T. C. and Joshi M. Indian J. Pure and Applied Phys. 48: 550 (2010)
  12. Litov E. and Uehling E. A. Phys. Rev. Lett. 21: 809 (1968)
    CrossRef
  13. Schmidt V. H. Ferroelectrics 73: 97 (1987)
    CrossRef
  14. Naithani U. C., Gairola R. P. and Semwal B.S. J. Phys. Soc. Jpn. 43: 204 (1977)
    CrossRef
  15. Deorani S. C, Naithani U. C. and Semwal B.S. Pramana J. Phys. 35: 181 (1990); J. Phys Chem. Solids 51: 1277 (1990).
  16. Dorogovtsv S. N. and Yushin N. K.Ferroelectrics 112: 27 (1990).
    CrossRef
  17. Hu Z., Garlend C. W. and Gonzalio Z. A. Ferroelectrics 112: 217 (1990)
    CrossRef
  18. Toda I. and Tatsuyaki I. J. Phys. Soc. Jpn. 31:1479 (1971); 42: 564 (1977)
  19. Fossum J.O., J. Phys. C 18: 5531 (1985).
  20. Scott J. F. JETP Lett. 49: 233 (1989)
  21. Levanyuk A. P. et. al. Zh. Eksp.Theor.Fiz 76:345 (1979)
  22. Fossum J. O. and Fossum K. J. Phys. C18:5549 (1985)
  23. Hu Z., Fossum J. O., Garland C. W. and Waller P. W. Phys. Rev. B33: 6331 (1986)
    CrossRef
Share Button

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

Designed by: Designtohost
Copyright © 2024 MSRI