Multiphase Phase-Field Approach for Virtual Melting: A Brief Review

Arunabha Mohan Roy

University of Michigan, Materials Science and Engineering, Ann Arbor, MI, 48109, USA

Corresponding Author E-mail: arunabhr.umich@gmail.com 

DOI : http://dx.doi.org/10.13005/msri/180201

ABSTRACT:

A short review on a thermodynamically consistent multiphase phase-field approach for virtual melting has been presented. The important outcomes of solid-solid phase transformations via intermediate melt have been discussed for HMX crystal. It is found out that two nanoscale material parameters and solid-melt barrier term in the phase-field model significantly affect the mechanism of PTs, induces nontrivial scale effects, and changes PTs behaviors at the nanoscale during virtual melting.

KEYWORDS: Ginzburg-Landau equations; Multiphase Phase-field theory; Virtual melting

Copy the following to cite this article: Roy A. M. Multiphase Phase-Field Approach for Virtual Melting: A Brief Review. Mat. Sci. Res. India;18(2).

Copy the following to cite this URL: Roy A. M. Multiphase Phase-Field Approach for Virtual Melting: A Brief Review. Mat. Sci. Res. India;18(2). Available from: https://bit.ly/3f87WwN

Phase-field (PF) approach ^{1, 2} has been widely used to captures various solid-solid phase transitions (PTs) ^3–11. Lately, it has been discovered that the finite-width interface plays a crucial role in controlling PTs for the different material systems ^{12, 13} such as PTs via intermediate molten state (IM ) which has been observed experimentally hundreds of degrees below the thermodynamic melting temperature in HMX ^{14, 15}. Such a transitional, metastable interface is called a virtual melt ^16–19. Additionally, it has been found that such virtual melt induces nontrivial scale effects, and changes phase transformation behaviors at the nanoscale ²⁰. Previously, a PF model was developed to describe solid-solid PT via IM in hyperspherical order parameter which is limited for n = 3 phase-system ²⁰. More recently, a multiphase phase-field (MPF) theory has been proposed for generalized n phase- system to capture such intriguing PT mechanism during virtual melting ²¹. This MPF model is thermodynamically consistent and satisfies all thermodynamic stability conditions ^21–24. One of the advantages of the MPF model is that, for each of the propagating solid-melt and solid-solid interfaces, the analytical solutions for width, energy, and velocity can be derived ^{21, 22, 25}. Thus, interface material properties can be fully calibrated and characterized for all interfaces. In the aforementioned MPF model, two dimensionless parameters at the nanoscale [e.g., ratios of width and energy of two different interfaces, kE (or ΔΨ) and kδ (or ΔΓ)] can be explicitly defined and controlled during PT. These parameters significantly affect the formation and stability of virtual melt during solid-solid PT in HMX ^21–24. The MPF approach has been employed to investigate the appearance and corresponding thermodynamic, and structure of IM for a three-phase system ^{22, 24}. Additionally, a detailed study on barrierless melt nucleation in HMX has been reported for propagating IM ²³. The kinematics and energetics of appearance of IM have been detailed in ²⁵. It is found out that the nanoscale material parameters and solid-melt barrier term in the MPF model significantly affect the mechanism of PTs, induces nontrivial scale effects, and changes PTs behaviors at the nanoscale during virtual melting ^{22–24, 26}.

In the abovementioned MPF model, order parameter’s (ηi) evolution has been described by Ginzburg-Landau (G-L) equations [21, 22] , where
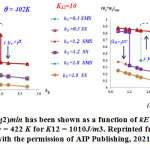
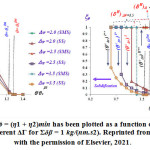
ψl = ψ˜θ + ψ˘θ + ψp is the local part of the Helmholtz free energy ψθ = ψl + ψ∇ (see [21, 22] for detail). In Fig. 1, different scale effects and non-trivial phase transformation mechanism has been observed when the influence of kE (or ΔΨ) which characterizes the energy of two different interfaces on the appearance and disordering of IM has been explored for two different non-equilibrium temperatures where ξϕ = (η1 + η2)min indicates the disordering. For different critical values of kE (i.e., kc  _E ) and depending on the energy barrier of the solid-melt interface K12 (or Σδβ ), two different solutions exist for kE < kc _E  for relatively low kδ (or ΔΓ) : one issolid-melt-solid interface solution with high disordering of IM at the interface , and another one is solid-solid interface solution with low disordering of IM at the interface. At first critical value k_E = (k_Ec )I , jump occurs between solid-melt-solid initial condition (SMS) solution to less disordered IM solution. Whereas, at second critical value k_E = (k_Ec )II , second jump occurs from solid-solid initial condition (SS) solution to high disordered IM solution. Hence, the solution of propagating inter facial melt can be either continuous-reversible without the hysteresis or jump-like first order discontinuous transformation with hysteresis. In Fig. 2, the influence of temperature on the appearance of propagating inter facial melt has been explored where ξϕ indicates the disordering. From the simulation results, it is clear that increasing temperature θ increases the disordering ξϕ of inter facial melt for all ΔΨ, ΔΓ (or kE, kδ ). For relatively small ΔΓ, the solution of ξϕ is continuous-reversible for both solid-melt-solid and solid-solid initial conditions. However, for relatively large ΔΓ, one is a solid-melt-solid interface solution with a high disordering of IM at the interface during solidification and another one is a solid-solid interface solution with low disordering of IM at the interface during melting at some critical value of temperature. These two different solutions correspond to two different nanostructures that produce a ”hysteretic region”. From the numerical result, it is evident that the appearance of nucleated melt can form much below thermodynamic melting temperature and different ΔΨ and ΔΓ control the width of the temperature hysteresis curve and melt formation temperature. The appearance of such nontrivial multiple solutions of IM could not be captured by the simplified thermodynamic descriptions which did not consider interface width as a scale parameter (i.e., kδ ), thus, can only predict a single solution of IM and the formation of IM (or melt) can only possible for kE > 2 close to thermodynamic equilibrium melt temperature.

Figure 1: ξϕ = (η1 + η2)min has been shown as a function of kE at (a) θ = 402 K and (b) θ∗ = 422 K for K12 = 1010 J/m3. Reprinted from ²²  with the permission of AIP Publishing, 2021.

Click on image to enlarge

Summarizing, the numerical results from the MPF model indicate a new perspective of solid-solid PT via transitive virtual melt in HMX. The penalizing potential in MPF formalism significantly controls the existence of virtual melt by limiting the pure solid-solid interface solution in order parameter space. Hence, these two scale parameters and penalizing term K12 (or Σδβ) influence the formation of virtual melt much below the thermodynamic melting temperature. The presented MPF model demonstrates the general applicability of this formalism to capture first-order jump-like PT as well as second-order continuous PTs. In addition, such MPF approach can be utilized to capture various PTs ²⁷ such as martensitic PTs ^{9–11, 28– 40}, evolution of nanovoids [41–44], surface-induced melting ^45–47, grain boundary premelting [48–53], interface modeling in composite [55], and crack propagation ^{56, 57}.

Figure 2:  ξϕ  = (η1 + η2)min  has been plotted as a function   of θ/θe for different  ∆Γ  for Σδβ = 1 kg/ (nm.s2).  Reprinted from ²³ with the permission of Elsevier, 2021.

Click on image to enlarge

Acknowledgment

The author is grateful to Dr. V. I. Levitas from Iowa State University, IA, USA for his kind guidance and discussion.

Funding Source

National Science Foundation (Grant No. CMMI-0969143).

Competing interests

The authors declare no competing interests.

References

1. L. Q. Chen, Phase-field models for microstructure evolution, Ann. Rev. Mater. Res. 32, 113-140 (2002)
   CrossRef
2. I. Steinbach, Phase-field models in materials science, Model. Sim. Mat. Sci. Eng. 17, 073001 (2009).
   CrossRef
3. A. Artemev, Y. Jin, A. G. Khachaturyan,Three-dimensional phase field model of proper martensitic transformation, Acta Mater. 49, 1165-1177 (2001)
   CrossRef
4. V. I. Levitas, D. L. Preston, Three-dimensional Landau theory for multivariant stress- induced martensitic phase transformations. I. Austenite ↔ martensite, Phys. Rev. B 66 (2002a) 134206.
   CrossRef
5. V. I. Levitas, D. L. Preston, Three-dimensional Landau theory for multivariant stress- induced martensitic phase transformations. II. Multivariant phase transformations and stress space analysis, Phys. Rev. B 66 (2002b) 134207.
   CrossRef
6. V. I. Levitas, D. L. Preston, D. W. Lee, Three-dimensional Landau theory for multivariant stress-induced martensitic phase transformations III. Alternative potentials, critical nuclei, kink solutions, and dislocation theory, Phys. Rev. B 68 (2003) 134201.
   CrossRef
7. V. I. Levitas and M.  Javanbakht, Surface tension and energy in multivariant martensitic transformations: phase-field  theory, simulations, and model of coherent interface Phy. Rev. Lett. 105 165701 (2010).
   CrossRef
8. V. I. Levitas and M.  Javanbakht,  Surface-induced phase transformations: multiple scale and mechanics effects and morphological transitions Phy. Rev. Lett. 107 175701 (2011) .
   CrossRef
9. V. I. Levitas, A. M. Roy, D. L. Preston, Multiple twinning and variant-variant transfor- mations in martensite: phase-field approach, Phys. Rev.B 88, 054113 (2013).
   CrossRef
10. A. M. Roy, Influence of interfacial stress on microstructural evolution in NiAl alloys, JETP Lett. 112, 173-179 (2020).
    CrossRef
11. A. M. Roy, Effects of interfacial stress in phase field approach for martensitic phase transformation in NiAl shape memory alloys, App. Phys. A 126, 576 (2020).
    CrossRef
12. M. A. Caldwell, R. D. Jeyasingh, H. P. Wong, D. J. Milliron, Nanoscale phase change memory materials, Nanoscale 4, 4382 (2012).
    CrossRef
13. S. Sinha-Ray, R. P. Sahu, A. L. Yarin, Nano-encapsulated smart tunable phase change materials, Soft Matter 7, 8823 (2011).
    CrossRef
14. B. F. Henson, L. B. Smilowitz, B. W. Asay, P. M. Dickson, The β − δ phase transition in the energetic nitramine octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazocine: Thermodyn-amics, J. Chem. Phys. 117, 3780 (2002).
15. L. B. Smilowitz, B. F. Henson, B. W. Asay, P. M. Dickson, The β − δ phase transition in the energetic nitramine octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazocine: Kinetics, J. Chem. Phys. 117, 3789 (2002).
    CrossRef
16. V. I. Levitas, R. Ravelo, Virtual melting as a new mechanism of stress relaxation under high strain rate loading, Proc. Natl. Acad. Sci. 109 (2012) 13204-13207.
    CrossRef
17. V. I.  Levitas,  B. F. Henson, L. B. Smilowitz, B. W. Asay, Solid-Solid Phase Transformation via Virtual Melting Significantly  Below the Melting Temperature, Phys. Rev. Lett. 92 (2004) 235702.
    CrossRef
18. V. I. Levitas, Crystal-amorphous and crystal-crystal phase transformations via virtual melting, Phys. Rev. Lett. 95 (2005) 075701.
    CrossRef
19. V. I. Levitas, Z. Ren, Y. Zeng, Z. Zhang, G. Han, Crystal-crystal phase transformation via surface-induced virtual premelting, Phys. Rev. B 85 (2012) 220104(R).
    CrossRef
20. V. I. Levitas, Effect of the  ratio of two nanosize parameters on the phase transformations, Scripta Mat. 149 155-162 (2018).
    CrossRef
21. V. I. Levitas, A. M. Roy, Multiphase phase field theory for temperature-induced phase transformations: Formulation and application to interfacial phases., Acta Mat. 105, 244- 257 (2016).
    CrossRef
22. A. M. Roy, Multiphase phase field  approach for solid-solid phase transformations via propagating interfacial phase in HMX., J. App. Phys. 129, 025103 (2021). https://doi.org/10.1063/5.0025867
    CrossRef
23. A. M. Roy, Barrierless melt nucleation at solid-solid interface in energetic nitramine octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazocine, Materialia 15 101000 (2021). https://doi.org/10.1016/j.mtla.2021.101000
    CrossRef
24. A. M. Roy, Formation and stability of nanosized, undercooled propagating interfacial melt during β → δ phase transformation in HMX nanocrystal, EPL (Europhysics Letters) 133 56001 (2021).https://doi.org/10.1209/0295-5075/133/56001
    CrossRef
25. A. M. Roy, Energetics and kinematics of undercooled nonequilibrium interfacial molten layer in cyclotetramethylene-tetranitramine crystal, Physica B: Condensed Matter 613, 412986 (2021). https://doi.org/10.1016/j.physb.2021.412986
    CrossRef
26. A. M. Roy, Influence of nanoscale parameters on solid-solid phase transformation in Octogen crystal: multiple solution and temperature effect, JETP Lett. 113, 265272 (2021). https://doi.org/10.1134/S0021364021040032
    CrossRef
27. V. I. Levitas, Phase transformations, fracture, and other structural changes in inelastic materials, Int. J. Plasticity 102914 (2020). DOI: 10.1016/j.ijplas.2020.102914
    CrossRef
28. M. Javanbakht, M. Adaei, Formation of stress- and thermal-induced martensitic na- nostructures in a single crystal with phase-dependent elastic properties, J. Mater. Sci. 55 (2019).
    CrossRef
29. A. M. Roy, Phase Field Approach for Multiphase Phase Transformations, Twinning, and Variant-Variant Transformations in Martensite, Doctoral dissertation 14635, Iowa State University, Ames (2015). https://doi.org/10.31274/etd-180810-4187
    CrossRef
30. S. E. Esfahani, I. Ghamarian, V. I. Levitas, P. C. Collins, Microscale phase fi  modeling of the martensitic transformation during cyclic loading of NiTi single crystal, Int. J. Sol. Struc. 146 (2018) 80-96.
    CrossRef
31. M. Javanbakht, M. Adaei, Investigating the effect of elastic anisotropy on martensitic phase transformations at the nanoscale., Comput. Mater. Sci. 167 (2019) 168-182.
    CrossRef
32. A. Basak, V. I. Levitas, Interfacial stresses within boundary between martensitic variants: Analytical and numerical finite   strain solutions for three phase field models, Acta Mat. 139 (2017) 174-187.
    CrossRef
33. V. I. Levitas, A. M. Roy, Multiphase phase field theory for temperature-and stress-induced phase transformations. Phys. Rev. B 91 (2015) 174109.
    CrossRef
34. S. Mirzakhani, M. Javanbakht, phase field analysis of austenitemartensite phase transformation at the nanoscale: Finite element modeling., Comput. Mater. Sci. 154 (2018) 4152.
    CrossRef
35. A. Basak,  V. I. Levitas,  Nanoscale multiphase phase field approach for stress-and temperature-induced martensitic phase transformations with interfacial stresses at finite strains., J. Mech. Phys. Solids 113 (2018) 162-196.
    CrossRef
36. M. Javanbakht, E. Barati, Martensitic phase transformations in shape memory alloy: phase field modeling with surface tension effect, Comput. Mater. Sci. 115 (2016) 137144.
    CrossRef
37. H. Babaei, V. I. Levitas, Stress-measure dependence of phase transformation criterion under finite strains: Hierarchy of crystal lattice instabilities for homogeneous and heterogeneous transformations, Phy. Rev. Lett. 124, (2020) 5701.
    CrossRef
38. H. Babaei, V. I. Levitas, Finite-strain scale-free phase field approach to multivariant martensitic phase transformations with stress-dependent effective thresholds, J. Mech. Phys. Sol. 144, (2020) 104114.
    CrossRef
39. M. Javanbakht, H. Rahbar, M. Ashourian, Explicit nonlinear finite element approach to the Lagrangian-based coupled phase fi and elasticity equations for nanoscale thermal- and stress-induced martensitic transformations Cont. Mech. Thermodyn. (2020) 1-20.
    CrossRef
40. A. M. Roy, Martensitic Nanostructure in NiAl Alloys: Tip Splitting and Bending., Mat.Sci. Res. 17, 03-06 (2020). https:dx.doi.org/10.13005/msri.17.special-issue1.02
41. M. Javanbakht, M.S. Ghaedi, Nanovoid induced martensitic growth under uniaxial stress: Effect of misfit strain, temperature and nanovoid size on PT threshold stress and nanostructure in NiAl, Comp. Mat. Sci. 184, (2020) 109928.
    CrossRef
42. A. Basak, V. I. Levitas, phase field study of surface-induced melting and solidification from a nanovoid: Effect of dimensionless width of void surface and void size, Appl. Phys. Lett. 112, (2018) 201602.
    CrossRef
43. M. Javanbakht, M. S. Ghaedi, Thermal induced nanovoid evolution in the vicinity of an immobile austenite-martensite interface, Comp. Mat. Sci. 172, (2020) 109339.
    CrossRef
44. M. Javanbakht, M. S. Ghaedi, Nanovoid induced multivariant martensitic growth under negative pressure: Effect of misfit strain and temperature on PT threshold stress and phase evolution, Mech. Mat. 151, (2020) 103627.
    CrossRef
45. V. I. Levitas, K. Samani, Coherent solid/liquid interface with stress relaxation in a phase field   approach to the melting/solidification  transition, Phys. Rev. B 84 (2011) 140103.
    CrossRef
46. V. I. Levitas and K. Samani, Size and mechanics effects in surface-induced melting of nanoparticles, Nature Com. 2 (2011) 1-6.
    CrossRef
47. V. I. Levitas, K. Samani, Melting and solidification of nanoparticles: Scale effects, thermally activated surface nucleation, and bistable states, Phys. Rev. B 89 (2014) 075427.
    CrossRef
48. Y. L. Lu, T. T. Hu, G. M. Lu, Z. Chen, Phase-field crystal study of segregation induced grain-boundary premelting in binary alloys. Physica B: Condensed Matter 451, 128 (2014).
    CrossRef
49. Y. H. Li et al. Thermally driven grain boundary migration and melting in Cu, The Journal of chemical physics 142, 054706 (2015).
    CrossRef
50. M. T. Rad, G. Boussinot, M. Apel, Dynamics of grain boundary premelting., Scientific Reports 10, 1-19 (2020).
    CrossRef
51. D. N. Sibley, P. Llombart, E. G. Noya, A. J. Archer, L. G. MacDowell, How ice grows from premelting films and water droplets. Nature Communications, 12, 1-11 (2021).
    CrossRef
52. S. Yang, N. Zhou, H. Zheng, S. P. Ong, J. Luo, First-order interfacial transformations with a critical point: breaking the symmetry at a symmetric tilt grain boundary. Phy. Rev. Lett., 120(8), 085702 (2018).
    CrossRef
53. R. K.Koju, Y. Mishin, Atomistic  study  of  grain-boundary segregation and grain-boundary diffusion in Al-Mg alloys, Acta Mat. 201 (2020) 596-603.
    CrossRef
54. H. Song, J. J. Hoyt, Barrier-Free Nucleation at Grain-Boundary Triple Junctions During Solid-State Phase Transformations, Phys. Rev. Lett. 117, 238001 (2016).
    CrossRef
55. A. M. Roy, Finite element modeling of three-dimensional multicomponent composite helicopter rotor blade for efficient design., Eng 2, 69-79 (2021). https://doi.org/10.3390/eng2010006
    CrossRef
56. V. I. Levitas, H. Jafarzadeh, G. H. Farrahi, M. Javanbakht, Thermodynamically consistent and scale-dependent phase field approach for crack propagation allowing for surface stresses, Int. J. Plast. 111, (2018) 135.
    CrossRef
57. H. Jafarzadeh, V. I. Levitas, G. H. Farrahi, M. Javanbakht, phase field approach for nanoscale interactions between crack propagation and phase transformation, Nanoscale. 11, (2019) 22243-22247.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.