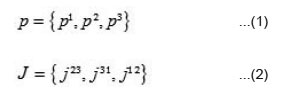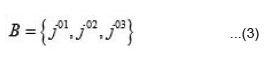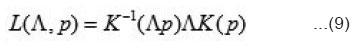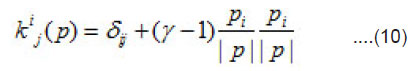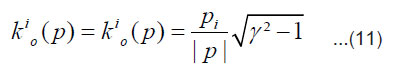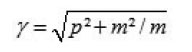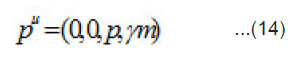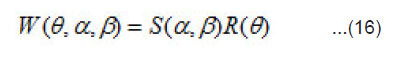Boosted Massive Particle and Corresponding Little Group Analysis in the Zero-Mass Limit

Mahendra Joshi*

Department of Physics, Govt. P.G. College, Ranikhet, Distt. Almora - 263 645, India.

DOI : http://dx.doi.org/10.13005/msri/070129

ABSTRACT:

Starting from massive particle case, we have obtained expression for the generator of little group for massless particle. It has also been shown that the non-compact generators, which appear in case of massless particles, can be carefully avoided in our case. Effective use of the Poincar algebra has been made to get the required result. Calculation has been done in a straightforward and simple manner.

KEYWORDS: Little group analysis; Massive particle; Zero-mass limit

Copy the following to cite this article: Joshi M. Boosted Massive Particle and Corresponding Little Group Analysis in the Zero-Mass Limit. Mat.Sci.Res.India;7(1)

Copy the following to cite this URL: Joshi M. Boosted Massive Particle and Corresponding Little Group Analysis in the Zero-Mass Limit. Mat.Sci.Res.India;7(1). Available from: http://www.materialsciencejournal.org/?p=2294

Introduction

The concept of the little group¹ has been introduced to construct states that transform properly under an arbitrary Lorentz transformation. Relativistic particles have their internal space-time symmetries or degrees of freedom. These symmetries for massive and massless particles can be correlated introducing concept of little group. Little group, in fact, is a subgroup of the Lorentz group. For the particles, with non-zero rest mass, the little group is three-dimensional rotation group O(3) . For massless particles the little group is Euclidian motion group ISO (2). Euclidian motion group is a semi-direct product of and – the group of translations in the 2-dimensional plane. Both the rotational group and determine the classification of particles on the basis of their spin quantum numbers. Two cases of physical interest namely massive particle case and massless particle case can be distinguished according to the non-zero and zero eigenvalues of the Casimir operator respectively. For each eigenvalue one can choose a standard four-momentum.² A little group element leaves this four-momentum invariant. Standard four-momentum can be chosen conveniently to suit the concerned case. In this way the little group structure can be determined explicitly for massive and massless particles. However one can obtain the little group as a particular limit of the three-dimensional rotation group by Inonu-Wigner group contraction.³ Aim of our paper is to present a simple line of action that can be followed to get exactly the same result which is obtained through Inonu-Wigner group contraction technique. We here, try to be more specific rather than being explicit to our problem.

Little Group Analysis

Space-time translations and Lorentz transformations are symmetries of Minkowski spacetime. Collectively they are parts of more general Poincare symmetry.

Space-time translations are generated by the energy-momentum four vector P^µ, and the Lorentz transformations are generated by the angular-momentum three-vector J and boost three-vector B. We can express them as [2]

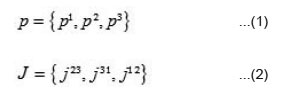
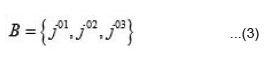
Here P^µ and J^µv are Hermitian operators P_µP^µ. Greek indices and run over the four space-time coordinate labels 1,2,3, and 0.

We mention two commutation relations among various components of these vectors as

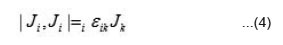
and

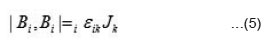
Where i, j, and k run over the values 1, 2, and 3, and ε_ijk is totally antisymmetric tensor with ε₁₂₃ = +1.

For a massive particle, the little group is the three-dimensional rotation group. Representations of the inhomogeneous Lorentz group can be derived from the representations of corresponding little group. Therefore, analysis of little group plays an important role in the study of the transformation of one-particle states under the action of inhomogeneous Lorentz group.

For massive particle case we can choose a standard four-momentum k^µ as [2]

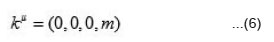
This standard four-momentum remains invariant under the action of corresponding little group element. As physical state- vectors are expressed in term of eigenvectors of the four-momentum P^µ, a standard Lorentz transformation is needed to get four-momentum from k^µ i.e

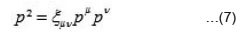
Here, we mention a Casimir operator P_μP^μ of Poincare symmetry which commutes with all Lorentz transformation operators. A one-particle state is its eigenstate with the eigen value P², given as 

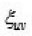
is spacetime metric with

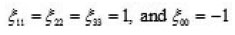
Equation (8) represents a quantity which remains invariant under a Lorentz transformation provided the principle of casuality is not violated [4].  As long as the velocity of a physical object is less than the velocity of light, this principal is not violated. 

The little group element in our case is given by [2]:

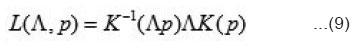
Where Λ represents homogeneous Lorentz transformation and k(p) is a standard boost which takes the standard four-momentum k^µ to p^µ. A convenient expression for this boost can be written as [2]

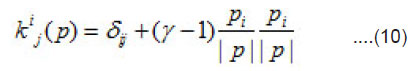
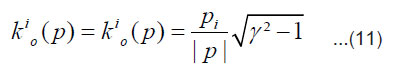
where

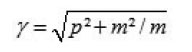
Using (8) we get

Now to simplify our line of action, we suppose that the particle is moving along the three-axis direction. This assumption does not alter the value of p² and an explicit expression for p^µ can be written as

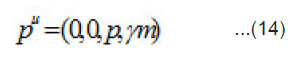
where |p|=p₃

As long as k^µ is not boosted, little group is O(3) like. Obviously a boosted four-momentum would be associated to a new little group. We are interested in such a transformation that leaves value of p² in (13) invariant. We can compare p² in (13) with the metric of Minkowski space.⁵ Here, in our case, we deal with a situation where the particle is boosted and massive. However, in the nonrelativistic limit, invariance of p² can be achieved.⁵ The transformation that keeps value of p² invariant belongs to a continuous, non-compact, and one-parameter Lorentz group.⁶ This group is like group of rotations through imaginary angles.⁶ Since the particle is in motion, the sole generator of this group can be identified with B₃, i.e third component of boost three- vector.² Obviously we have B₁=B₂ When particle velocity reaches to ultimate speed c, p² in (13)  no longer remains a physically realizable quantity. Only sensible substitution we can do is to put m = 0 in (13). Hence we have

This condition is related to massless particle [2].

As we have mentioned earlier, little group for massless particle must be different. To get its structure we make use of (4) and (5). Representations of inhomogeneous Lorentz group and corresponding little group are closely related, and so are their respective group algebras. Therefore, as we have B₁ and B₂ absent, (4) and (5) show that J₁ and J₂ should also be absent. Now, the only generator left is J₃. Since in massive particle case, little group was three-dimensional rotation group, the little group generators were J₁, J₂, and J₃. Now in the limit of boosted massive particle, with m=0, we have J₁ and J₂ equal to zero, so only generator of new little group would be J₃ alone. At this point we compare our result with [2]. Expression for most general element of little group for massless particle is given as

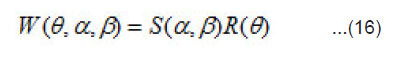
Where θ, α and β are the parameters of corresponding little group ISO(2) , consisting of translations and rotations in two dimensions. Generators of this group are N₁, N₂ and J₃, where

Now, whether it is nature’s constraint or our incapability to deal with such a situation, we are here forced to set these non-compact generators equal to zero. Then the only remaining generator is the rotation around three-axis J₃, which is nothing but the helecity of the particle. Here we notice that setting N₁ and N₂ equal to zero is an absolute necessity as long as we are dealing with observed massless particles of integer and half-integer helecities. As for treating N₁ and N₂ as gauge generators,^7-10 leading to electromagnetic gauge invariance, we differ altogether with the established facts. As long as N₁ and N₂ are parts of the little group, treating them as generators of gauge invariance and simultaneously setting them equal to zero is not justified.

Conclusions

Our analysis is, to show how to get the little group generator for massless particle in a simple way. Non-compact generators are not present and we make no additional assumption to set them equal to zero. A comparison has also been made between our line of action and the standard procedure. It has been found that, comparatively, we are in advantageous position to get the same result and yet not setting the non-compact generators equal to zero.

References

1. E.P. Wigner. Ann. Math. 40, 149 (1939).
   CrossRef
2. S.Weinberg. The Quantum Theory of Fields. Cambridge University Press, Cambridge 1 (1996).
   CrossRef
3. E. Inonu, E. P. Wigner. Proc. Natl. Acad. Scie. (U.S.A) 39, 510 (1953).
   CrossRef
4. J. D. Jackson. Classical Electrodynamics. Ed. John Wiley, Singapore (1999).
5. G. B.Arfken, H. J. Weber. Mathematical Methods for Physicists. Academic Press, California (2005).
6. A. W. Joshi. Elements of Group Theory for Physicists. New Age International (P) Limited, New Delhi (1997).
7. S.Weinberg. Phys. Rev. B 134, 882 (1964).
   CrossRef
8. S.Weinberg. Phys. Rev. B 135, 1049 (1964).
   CrossRef
9. D.Han, Y. S. Kim, and D. Son. Phys. Rev. D 26, 3717 (1982).
   CrossRef
10. D. Han, Y.S. Kim, and D. Son. Phys. Rev. D 31, 328 (1985).
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.