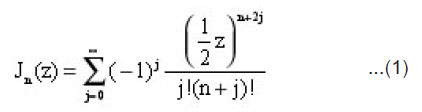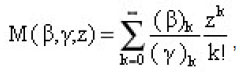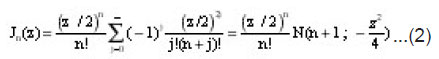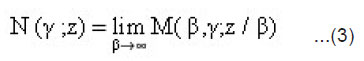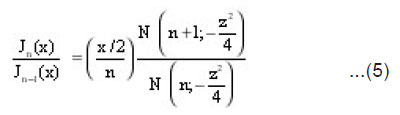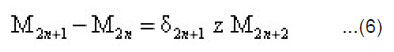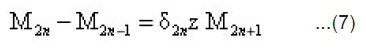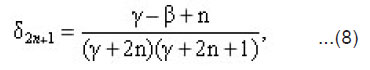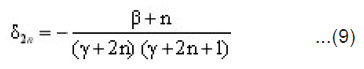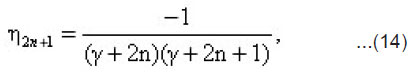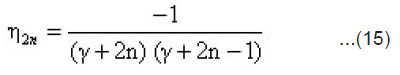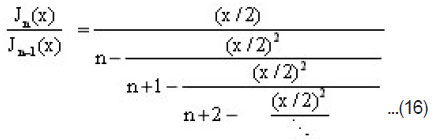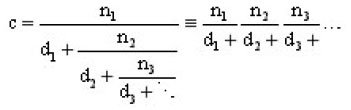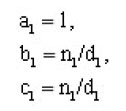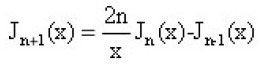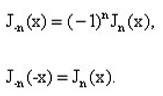Continued Fraction Evaluation of Jn (X)/Jn-1 (X)

A. S. Al-Fhaid*

Department of Mathematics, College of Sciences, P.O.Box 80203, King Abdulaziz University, Jeddah-21589, Saudi Arabia.

DOI : http://dx.doi.org/10.13005/msri/070109

ABSTRACT:

In this paper, continued fraction expansion for the Bessel funcions ratio J_n (x)/J_n-1 (x) was developed. An efficient and simple computational algorithm based on this expansion was also developed using top-down evaluation procedure.Numerical results of the algorithm are in full agreement at least to fifteen digits accuracy with that of the standared tables.

KEYWORDS: Bessel functions; Continued fraction; Special functions; Number theroy

Copy the following to cite this article: AL-FHAID A. S. Continued Fraction Evaluation of Jn (X)/Jn-1 (X). Mat.Sci.Res.India;7(1)

Copy the following to cite this URL: AL-FHAID A. S. Continued Fraction Evaluation of Jn (X)/Jn-1 (X). Mat.Sci.Res.India;7(1). Available from: http://www.materialsciencejournal.org/?p=2229

Introduction

Bessel functions of the first kind of order n is defiend as [e.g. Refaat El Attar 2007] :

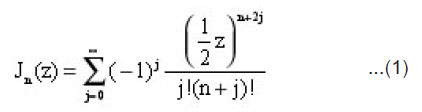
J_n (z) has a branch cut discontinuity in the complex z plane running from -∞ to 0.

The Bessel functions are central to many calculations in mathematical physics,for example they arises when finding separable solutions to Laplace’s equation and the Helmholtz equation in cylindrical or spherical coordinates. Therefore, Bessel functions especially important for many problems of wave propagation, static potentials, and so on.Also ,in space dynamics, Bessel functions are extremly important in the expansion theory of elliptic motion [Battin 1999].

There are several methods available for the evaluation of Bessell functions [Watson 1995]. In fact ,continued fraction expansions are, generally, far more efficient tools for evaluating the classical functions than the more familiar infinite power series. Their convergence is typically faster and more extensive than the series. Due to the above importance of Bessel functions, and on the other hand, due to the efficiency of the continued fraction for evaluating functions are what motivated the present work: to establish computational algorithm for J _n (x) / J _n−1 (x) based on its continued fraction expansion.

Continued Fraction of J_n (x)/J_n-1 (x)

The confluent hypergometric functions M(β,γ;z) are defined [Abramowitz and Stegun 1970] as:

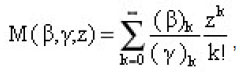
where

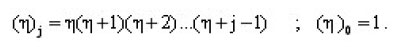
From Equation(1)  it follows that

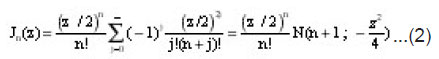
where

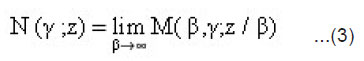
consequently

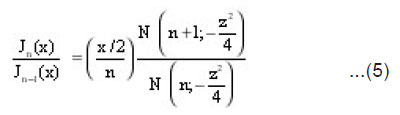
It was shown that [Sharaf  2006]

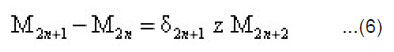
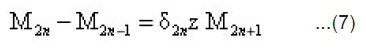
where

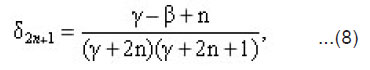
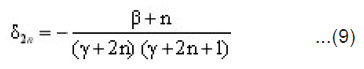
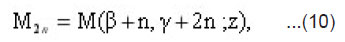
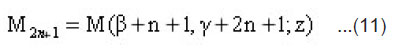
and

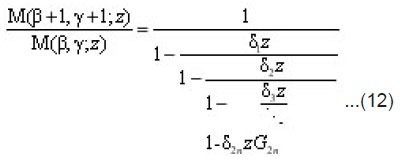
Now applying the limiting process of Equation(3) we get :

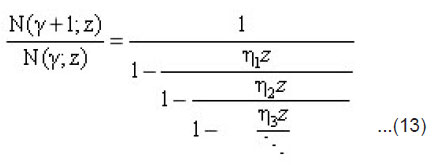
 where

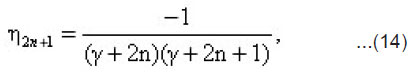
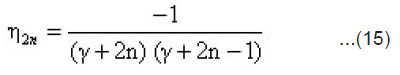
Finally ,it follows from Equations (5) and (13) ,that

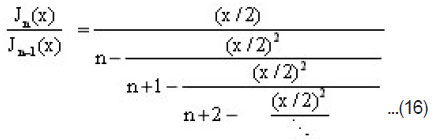
Computational Developments Top-Down Continued Fraction Evaluation

There are several methods available for the evaluation of continued fraction. Traditionally, the fraction is either computed from the bottom up, or the numerator and denominator of the nth convergent were accumulated separately with three-term recurrence formulae. The draw-back to the first method is, to decide far down the fraction to being in order to ensure convergence . The drawback to the second method is that the numerator and denominator rapidly overflow numerically even though their ratio tends to a well defined limit. Thus, it is clear that an algorithm which works from top down while avoiding numerical difficulties would be ideal from a programming standpoint.

Gautschi [1967] proposed a very concise algorithm to evaluate continued fraction from the top down and was applied very successfully for the initial value problem[Sharaf and Sharaf 2003]. Gautschi ‘s algorithm may be summarized as follows. If the continued fraction is written as

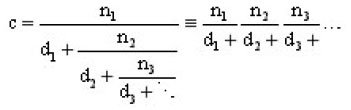
then initialize the following parameters

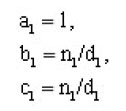
and iterate (k=1,2,…) according to

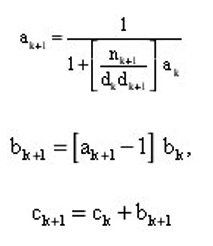
In the limit, the c sequence converges to the value of the continued fraction

Numerical Results

Top-down continued fraction algorithm was applied for the function J_n (x)/J_n-1 (x) [Equation(16)] to construct Table I of Appendix A for some real poisitive values. of n . Within fiffteen digits accurcy,our results agree completey with those given in[Abramowitz, M.and Stegun 1970]

Scheme 1

Click on image to enlarge

 Scheme 2

Click on image to enlarge

 Scheme 3

Click on image to enlarge

 Table 1: Values of Jn (x)/Jn-1 (x) using continued fraction

Click on image to enlarge

Conclusion

In conculding the present paper. An efficient and simple computational algorithm for the functin 

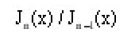
 was establised using continued fraction expansion. Numerical results of the algorithm are in full agreement at least to fifteen digits accuracy with that of the standared tables.

In addition ,there are many applications of our alogrothm, of these are, if the value of

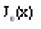
is known, then

 

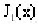
is computed from the above algorthim, these two values of

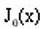
and can be used to compute,

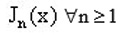
using the known recuurence formula:

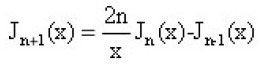
moreover ,for vegative values of n and x we can use:

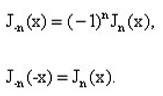
Finally, the corresponing analysis for the modified Bessell function can be obtained using the identity

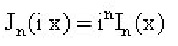
where

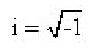
References

1. Abramowitz, M.and  Stegun, I.A. (ed.) “Handbook of Mathematical Functions”, Dover Publications,Inc.,New york (1970 ).
2. Battin, R.H. “An Introduction to the Mathematics and Methods of Astrodynamics”  AIAA Education Series ,American Institute of Aeronautics and Astronautics,Inc (1999). 
3. Gautschi,W., “Computational Aspects of Three-Term Recurrence Relations”,SIAM Reviw, 9(1): (1967).
4. Refaat El Attar, “Bessel and Related Functions” .Lulu Press Inc. ,USA (2007).
5. Sharaf, M.A. “Computations of the Cosmic Distance Equation” Appl.Math.Comput. 174: 1269-1278 (2006).
   CrossRef
6. Watson, G. N., A Treatise on the Theory of Bessel Functions, Second Edition, Cambridge University Press,UK (1995).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.