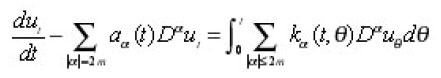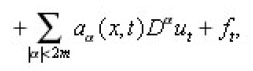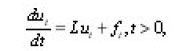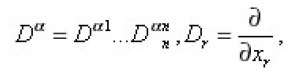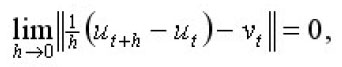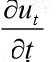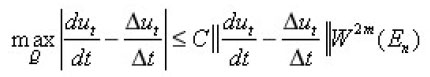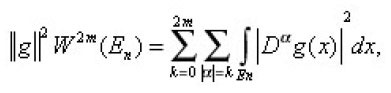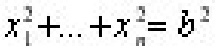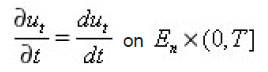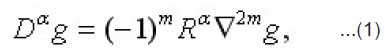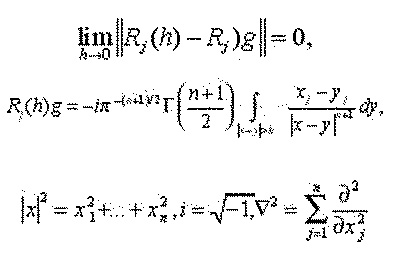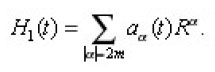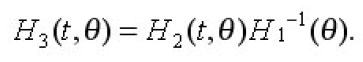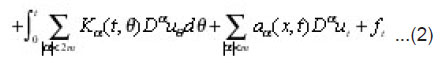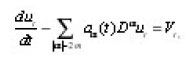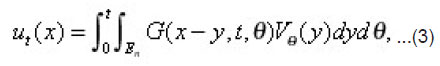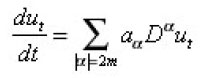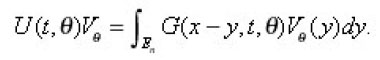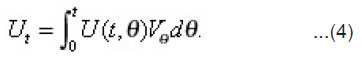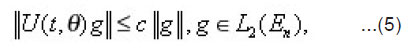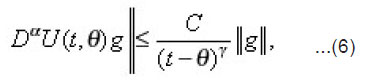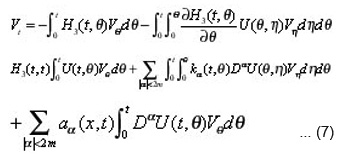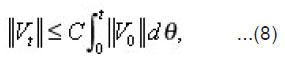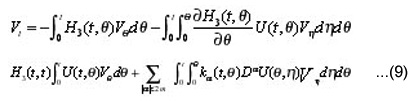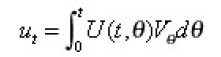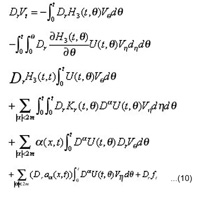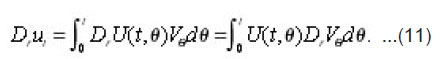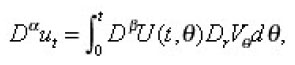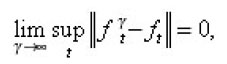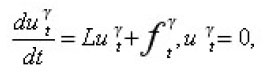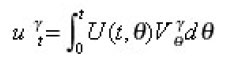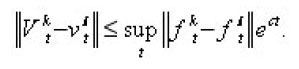Some Study of a Cauchy Problem in Parabolic Integrodifferential Equations Class

A. S. Al-Fhaid

Department of Mathematics, College of Sciences, P.O.Box 80203 King Abdulaziz University, Jeddah - 21589, Saudi Arabia.

DOI : http://dx.doi.org/10.13005/msri/070111

ABSTRACT:

We consider the parabolic integrodifferential equations of a form given below. We establish local existence and uniqueness and prove the convergence in L₂(E_n) to the solution U_t of the Cauchy problem.

KEYWORDS: Cauchy; Parabolic; Integrodiffrential equationss; Operator

Copy the following to cite this article: AL-FHAID A. S. Some Study of a Cauchy Problem in Parabolic Integrodifferential Equations Class. Mat.Sci.Res.India;7(1)

Copy the following to cite this URL: AL-FHAID A. S. Some Study of a Cauchy Problem in Parabolic Integrodifferential Equations Class. Mat.Sci.Res.India;7(1). Available from: http://www.materialsciencejournal.org/?p=2235

Introduction

Let’s have the parabolic integrodifferential equations of the form

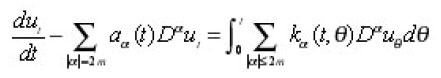
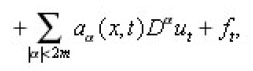
where  the  partial differential operator   

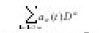
is uniformly elliptic,

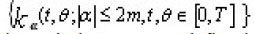
is a family of linear bounded operators defined on the space of all square  integrable  functions L₂(E_n) and E_n is the n- dimensional Euclidean space.

We consider integrodifferential equations of the form;

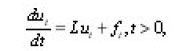
Where,

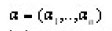
is an n-dimensional multi index,

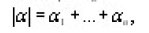
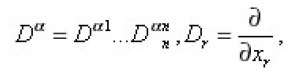
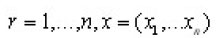
is an element of the n-dimensional Euclidean space E_n.  Let L₂(E_n) be the space of all square integrable function on E_n and W^m(E_n)  the Sobolev space, [ the space of all functions 

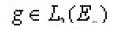
such that he distributional derivative

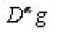
 with 

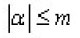
all belong to 

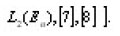
We assume that u_t  satisfy the Cauchy condition;

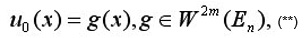
We can assume that on g(x)=0 on E_n. We shall say that u_t is of the class S if for each

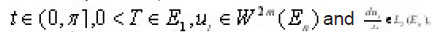
where

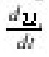
 is the abstract derivative of u_t in L₂(E_n) in other word there is and element 

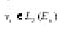
such that

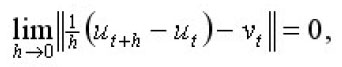
Where

is the norm in 

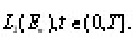
Notice that if 

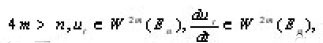
for each 

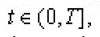
  then the partial derivative 

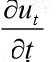
exists in the usual sense

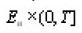
 and 

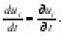
in fact according to the embedding theorem [3], [8], we have

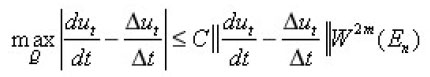
Where

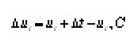
is a positive constant,

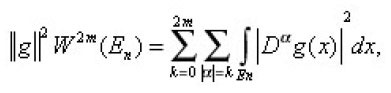
is the volume enclosed by the sphere 

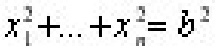
 letting 

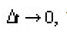
we get 

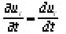
on Q x (0, T)

Since b is arbitrary, it follows that

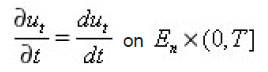
Let us suppose that the following assumptions are satisfied; 

The coefficients 

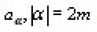
 are real functions of t, defined on [o,T] and having continuous derivatives

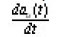
 on [o, T]

The deferential operator 

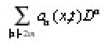
is uniformly elliptic on [o, T]

The kernels

 

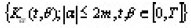
are linear bounded operators acting on into it self. It is assumed that these operators are continuous in

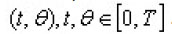
Furthermore it is assumed that the (abstract) partial derivatives 

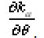
 exist  for all 

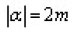
and represents linear bounded operators on L₂(E_n) which are continuous in

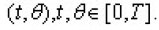
The coefficients 

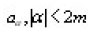
are real functions, which are continuous  and bounded on 

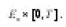
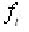
is a map from [0,T] into which is continuous in t with respect to the norm in

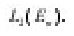
All the coefficients 

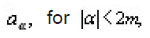
have continuous bounded partial derivatives

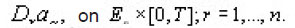
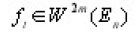
The range of the operators 

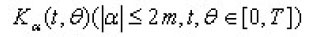
is the space

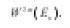
 we assume that all the operators 

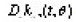
are bounded, and that 

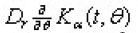
 exist for all 

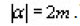
The operators

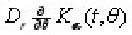
 are supposed to be bounded and continuous in 

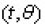
 for all

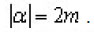
 It is supposed also that 

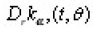
are continuous in 

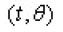
Proposition 1.

Under conditions (a) , …. , (e) if there is at least one solution in the class S of the Cauchy problem (*), (**), then this solution is the unique such solution.

Proof.

 If 

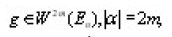
then we have the following representation:

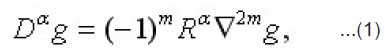
Where

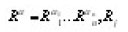
is the singular integral operator defined to be the

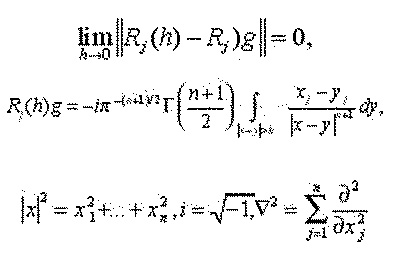
and

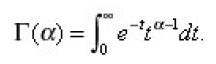
Notice that 

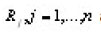
 are bounded operators from L₂(E_n) into itself, [1],[2].

Let H₁(t)  be an operator defined by

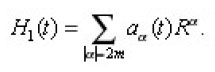
According to assumption, the operator H₁(t) has a bounded inverse 

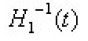
defined on for every

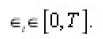
Set

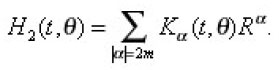
and

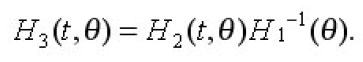
Using (1), then equation (*) can be written in the form;

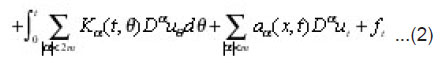
To Prove the uniqueness of the considered Cauchy problem, we set

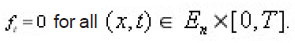
Now set

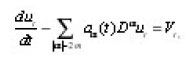
Then according to assumptions (1) and (2), we can write

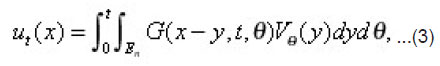
Where G is the fundamental solution of the Cauchy problem for the parabolic equation

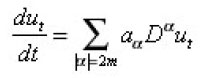
Let

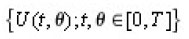
be the family of bounded operators defined by

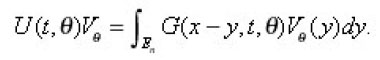
Consequently (3) can be written in the form

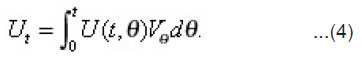
According to the well-known properties of the fundamental solution G, [4], [5], we can see that

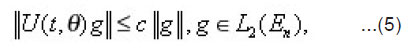
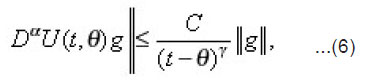
For

 

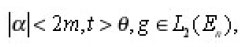
where C is a positive constant and is a constant satisfying 0<y<1. Substituting from (4) into (2), we get

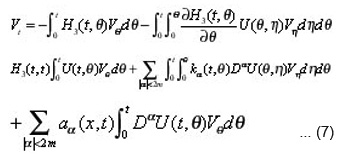
Using (5) and (6), we get from (7), the following estimation;

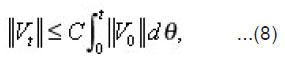
(To obtain (7) and (8), we already used conditions (c) and (d) where C is a positive constant. Thus (4) and (8) lead immediately to the fact that u_t(x)=0 on E x [0,T].

Proposition2

Under the condition (a) , …, (h) the solution of the Cauchy problem (*) , (**) exists in the class S.

Proof
Using the conditions from (a) to (e), we obtain

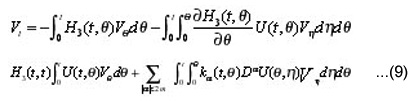
According to (5) and (6), the Volterra integral equation (9) has a unique solution t V in which satisfies:

where c is a positive constant.

This means that under conditions from (a) to (e), we can obtain the so called mild solution [6] of the Cauchy problem (*) , (**). this solution is represented by

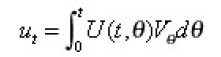
Now we must prove that the distributional derivatives

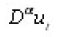
 exists in L₂(E_n) for all 

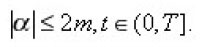
To prove that 

 

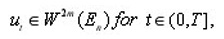
we apply formally the differential operator on both sides of the integral equation (9), then we get;

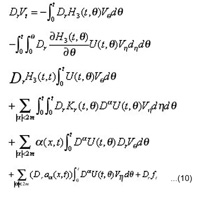
Let us consider as the unknown element in the integral equation (10). Under the assumptions (a),…, (h) this integral equation can be solved for

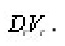
Thus

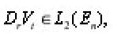
for

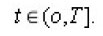
Now we have

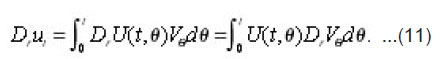
Using (11), we can wire

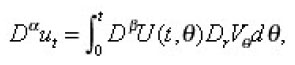
Where

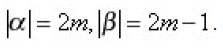
Proposition 3

Let 

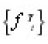
L₂(E_n) for every 

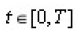
and continuous in t. suppose.

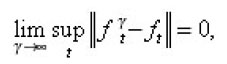
Where

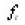
 is continuous in 

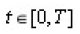
if is a sequence of functions of the class S, which are solutions of the Cauchy problem

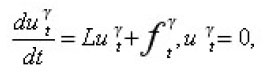
then

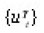
 converges in L₂(E_n) to the solution of the Cauchy problem (*), (**).

Proof. Set

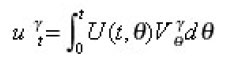
We find

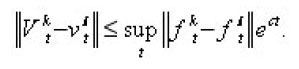
References

1. A.S. Al-Fhaid, The Derivation of Interstellar Extinction Curves and Modelling, Ph.D. Thesis.
2. A. S. Al-Fhaid, Continued fraction Evaluation of the Error function. To appear.
3. Calderon H. P., Zygmond A. Singular Integral Operators and Differential Equations II, Amer J. Math., 79,(3); (1957).
4. EhrenperiesL, Cauchy’s Problem for linear Differential Equations with constant coef-ficients II, Proc. Nat. Acad. Soi USA, 42. Nv. 9.
5. El-Borai. M. On the correct formulation of the Canchy problem Vesnik Moscow univ. 4 (1968).
6. Friedman A. Partial differential Equations, Robert E. Krieger Publishing Company, New York, 101-102 (1976).
7. Hormander L. , Linear partial differential Operators ( Springer – Verlag) , Berlin, New York (1963).
   CrossRef
8. Samuel M. R., Semilinear Evolution equations in Banach spaces with applications of Parabolic partial differential Equations, Trous Amer. Math. Soc. 33: 523-535 (1993).
9. Yosida K. Functional Analysis, Spreinger verlage, (1974).

---

This work is licensed under a Creative Commons Attribution 4.0 International License.